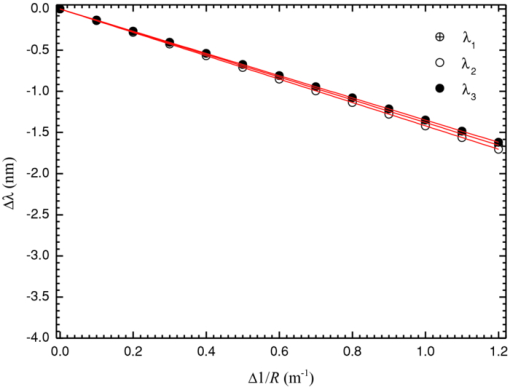
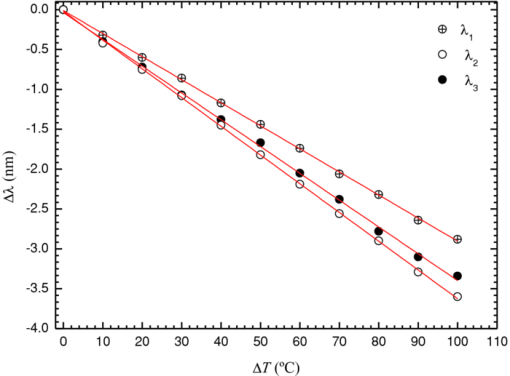
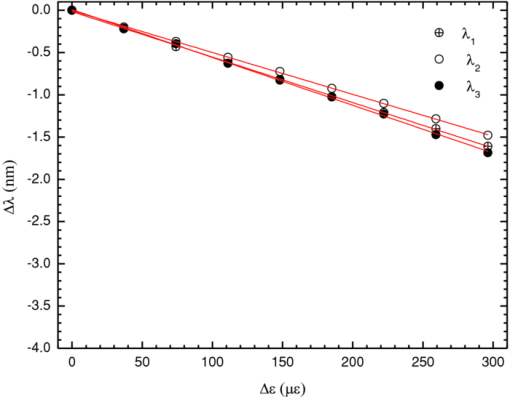
1.

Introduction

The twin-core fiber was first demonstrated as a temperature sensor in 1983 by Meltz ¹ The temperature sensitivity of a twin-core fiber sensor with a single cladding and the circular cores is due almost entirely to the linear expansion of the core and the thermo-optic effect. Peng ² fabricated a twin-core optical fiber with a large elliptical core with significant polarization-dependent coupling properties. On the other hand, Tjugiarto ³ observed that the coupling between the two cores increases with the spin rate in a spun twin-core fiber. In 2000, Gander ⁴ proposed a two-axis bend measurement using multicore optical fiber. MacPherson ⁵ demonstrated a curvature sensor using a twin-core photonic crystal fiber, and Flockhart ⁶ reported two-axis bend measurement using Bragg gratings written in multicore optical fiber.

In this work, the authors propose a new sensing head based on a Mach–Zehnder interferometric configuration using a suspended twin-core fiber. This sensing head presents different sensitivities when subjected to strain, curvature, and temperature. The possibility of simultaneous measurement using the matrix method to discriminate the three parameters is also demonstrated.

2.

Experimental Setup and Results

Figure 1 presents the experimental setup with the sensing head based on a suspended twin-core fiber. Light from a broadband source in the 1550-nm window was linearly polarized with a polarizer and injected into the suspended twin-core fiber with a length of 33 cm. A polarization controller was used to optimize the polarization states (x- and y-axes), and all the measurements were performed with an optical spectrum analyzer. The fiber cross section is shown also in Fig. 1. The suspended twin-core fiber with four holes made of pure silica was fabricated at the Institute of Photonic Technology (Jena, Germany). The distance between the two cores is ∼6.4 μm, being possible to simultaneously illuminate the two cores using a standard single-mode fiber (SMF-28^®). The core's diameter is 1.5 μm, the cladding is 124 μm, and the big and small holes are 10 and 5 μm, respectively.

Fig. 1

Experimental setup of the Mach–Zehnder interferometric configuration based on the suspended twin-core fiber and photos of the fiber cross section.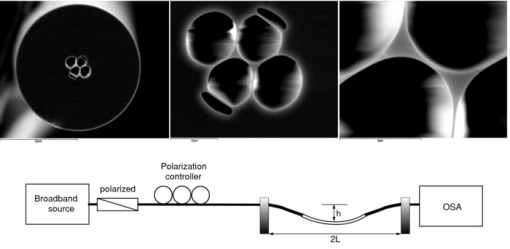

Because of the fiber geometry, the triangular-shaped cores in the suspended twin-core fiber presents birefringence and two discrete Mach–Zehnder interferometers can be excited. The first interferometer is obtained when the polarized light excites only the x-polarization state in the two cores. The second interferometer appears when the input linear polarized light is along the y-axis. In these situations, we have a single Mach–Zehnder interferometer, where each arm is an eigenaxis of each core, originating a typical two-wave channeled spectrum, which can be observed in Figs. 2 and 2. When the input polarized light is along a direction that excites the two eigenaxes of the two cores, a beat of the two single interferometers appears, as is evident in Fig. 2.

Fig. 2

Spectral response of the interferometric structure for input polarized light along the (a) x-axis, (b) y-axis, and (c) when both axes of the two cores are excited.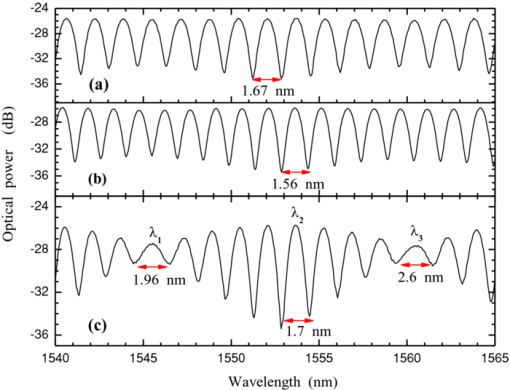

From the channeled spectrum periodicity [Figs. 2 and 2], it turns out that the effective refractive index difference for the light propagating in the two cores is 7.6 × 10⁻⁴ (x polarization) and 8.1 × 10⁻⁴ (y polarization) in the 1550-nm wavelength region.

Because of the small diameter of the cores, there is a substantial evanescent field of the propagating light. Consequently, the waveguide dispersion is not negligible, which is evident from the data shown in Fig. 2, particularly in the case of excitation of the two x- and y-polarization Mach–Zehnder interferometers, as is clear in Fig. 2. Around the wavelengths λ₁ ∼ 1546 nm, λ₂ ∼ 1554 nm, and λ₃ ∼ 1560 nm, the periodicity of the channeled spectrum is ∼1.96, ∼1.70, and ∼2.60 nm, respectively. Also, it was observed that the dependence with curvature, strain, and temperature of the peaks associated with these three wavelengths were all different, providing an opportunity to perform simultaneous measurement of these three parameters.

To test this possibility, first the behavior of this structure as a curvature sensor was characterized.⁷ Hence, the fiber was fixed at two points at a distance of 540 mm from each other and submitted to specific curvature values by using a translation stage (via successive 100–μm displacements). The spectral position of the maximums associated with λ₁, λ₂, and λ₃ have different and linear responses to curvature variations, as shown in Fig. 3, with sensitivity coefficients of (–1.38±0.07) nm/m⁻¹, (–1.42±0.07) nm/m⁻¹, and (–1.35 ±0.05) nm/m⁻¹, respectively.

Fig. 3

Dependence on curvature of the peaks associated with λ₁, λ₂, and λ₃ in Fig. 2.

The response to temperature variations of the sensing head was also characterized.⁸ The structure was placed in a tube furnace and submitted to increasing values of temperature in the range 0–100°C, with 10°C steps. The results shown in Fig. 4 indicate that the wavelength peaks λ₁, λ₂, and λ₃ have linear responses to temperature variations, characterized by the sensitivities: (28.2±0.8), (34.9±0.8), and (33.5±0.8) pm/°C for λ₁, λ₂, and λ₃, respectively.

Fig. 4

Dependence on temperature of the peaks associated with λ₁, λ₂, and λ₃ in Fig. 2.

The sensing structure was also characterized in terms of strain. The input and output fibers were accordingly fixed at two points 540 mm apart and submitted to specific strain values by using a translation stage (via successive 10-μm displacements). The results are made available in Fig. 5. Once again, the wavelength peaks have linear responses to strain variations, with sensitivities: (5.4±0.01), (5.0±0.01), and (5.6±0.01) pm/μɛ, for λ₁, λ₂, and λ₃, respectively.

Fig. 5

Dependence on strain of the peaks associated with λ₁, λ₂, and λ₃ in Fig. 2.

The sensitivity coefficients obtained for curvature, temperature, and strain applied to the proposed sensing structure indicates the feasibility to perform simultaneous measurement of these measurands. From the experimental sensitivity coefficients, comes the following:

3.

Conclusions

A new sensing head based on a Mach–Zehnder interferometric configuration based on a suspended twin-core fiber was proposed. Because of the birefringence of the cores, in the presence of input light with a polarization state that excites the two eigenaxes of the two cores, a double interferometer is present, originating beat phenomena. Because of the waveguide dispersion of the light that propagates in the cores, the variation with curvature, temperature, and strain of a particular fringe of the beat channeled spectrum depends on the wavelength. This feature opens the possibility of simultaneous measurement of these three parameters.