|
|
1.IntroductionImaging spectrometers collect data over three dimensions—two spatial and one spectral —so that the complete dataset is typically referred to as a datacube. The most common method for categorizing the various types of imaging spectrometers is by the portion of the datacube collected in a single detector readout. “Whiskbroom” spectrometers, which use a linear array of detectors, collect a single column of the datacube at a time and thus scan across the two spatial dimensions of the datacube (see Fig. 1).1 “Pushbroom” spectrometers use a 2D detector array, and thus collect a vertical slice of the datacube at once so that only one spatial dimension needs to be scanned to fill out the cube.2 A filtered camera, constructed by placing a filter wheel or tunable spectral filter in front of a camera, collects a horizontal slice and thus needs to scan along the spectral dimension to complete the data set.3 Other scanning modalities exist, such as Fourier Transform imaging spectrometry (FTIS), but these can be shown4,5 as equivalent to one of the above categories—in this case, the filtered camera. Fig. 1The portions of the datacube collected during a single detector integration period for (a) scanning, and (b) snapshot devices. 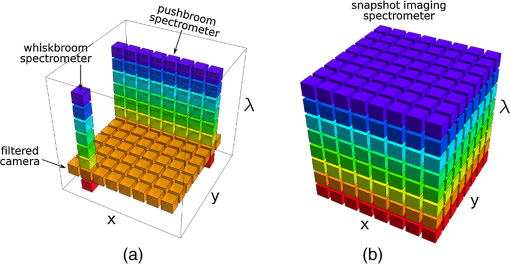 “Snapshot” imaging spectrometers, in contrast, collect the entire 3D datacube in a single integration period without scanning. While the existing literature cites advantages for snapshot instruments such as the lack of scanning artifacts and the increased robustness or compactness due to the lack of moving components,6 these qualities are actually secondary to the main benefit of snapshot collection, which has been given little attention. This is the advantage in light collection (optical throughput), which can be dramatic for larger datacubes. As a parallel to the Jacquinot (throughput) advantage and the Fellgett (multiplex) advantage nomenclature commonly used in spectrometry, we call this the snapshot advantage. While discussion of the light collection advantages of snapshot imaging spectrometers has had some exposure in the astronomy community,7–9 discussion has been limited to instruments coupled to astronomical telescopes. As a result, few outside the astronomy community (excepting only Refs. 10 and 11) are even aware of this important issue,12 which has not even been given a name. We provide below the first comprehensive discussion of its characteristics across all modalities. 2.Snapshot Advantage FactorThe snapshot advantage factor is easily derived from knowledge of the datacube dimensions and the measurement architecture. For example, for a datacube of dimensions , a whiskbroom (point scanning) system sees only 100 voxels of the datacube at any given time. If the remainder of the object is emitting light during this period, then all light emitted outside these 100 voxels is lost. The overall light collection efficiency from geometric considerations alone is thus the inverse of the number of elements in the scan—in this case . This value is cripplingly low for all but the most forgiving of experiments. For a pushbroom (line scanning) system, one sees a slice of the datacube at a given time, so the maximum full-cube efficiency value is . While many experiments can tolerate such a low efficiency, dynamic scenes prevent the longer integration times needed to overcome this poor light collection. Since the scan dimension in our example is one fifth that of the spatial dimensions, filtered cameras have the potential to provide a five-fold improvement in light collection ability. In practice, however, this is typically offset by light losses due to dead time between scan points or to low transmission in the spectral filters (see, for example, Ref. 13). Ignoring these losses, the geometric efficiency still remains low, at . These efficiency values given for scanning devices have been obtained by geometric considerations alone. Not all snapshot instruments take advantage of this improvement in light collection, however. In terms of light collection capacity, one can divide snapshot techniques into two broad categories—“full-throughput” and “throughput-division” techniques—based on whether or not they sacrifice light based on their geometry. That is, although all snapshot systems remove the need to scan, and thus do not have the efficiency loss associated with scanning across elements, throughput-division snapshot implementations suffer from the same light collection tradeoffs as their scanning counterparts. For example, the multiaperture filtered camera14–17 [a division of aperture (DoAp) technique, see Fig. 2(a)] consists of an array of mini-cameras each with its own spectral filter. The efficiency of each individual mini-camera, however, is reduced to because of the bandpass filters used. A second example is the multispectral filter array camera18,19 [a division of focal plane technique, see Fig. 2(b)]. This system uses a single monolithic lens for light collection, but places filters over each individual pixel in order to spectrally resolve light in the image. This technique thus sacrifices a fraction in pixel fill factor, for any individual wavelength band in the datacube. The fraction of is thus a fundamental geometric limit to light efficiency for these techniques. Due to the use of filters in both of these architectures, the light collection efficiency is thus no better than for equivalent scanning systems. Fig. 2System architectures for snapshot spectral techniques: (a) division of aperture (DoAp) multiaperture filtered camera, and (b) division of focal plane (DoFP) the multispectral filter array camera. 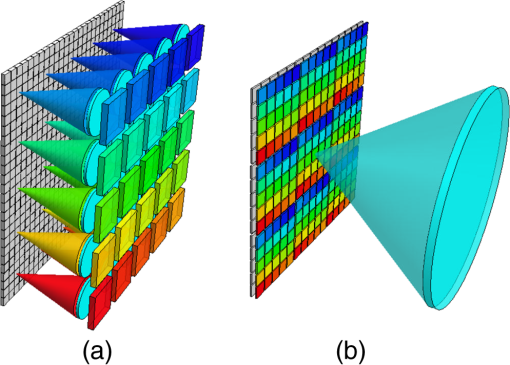 Full-throughput snapshot techniques, on the other hand, have no filters, and thus no fundamental geometric tradeoffs in light collection. There is a remarkable variety of architectures available for full-throughput imaging spectrometers, among which are (in order of provenance) computed tomographic imaging spectrometry20 (CTIS), fiber-reformatting imaging spectrometry (FRIS),21,22 integral field spectroscopy with lenslet arrays23 (IFS-L), integral field spectroscopy with image slicing mirrors24 (IFS-S), image-replicating imaging spectrometry11 (IRIS), filter stack spectral decomposition25 (FSSD), coded aperture snapshot spectral imaging26 (CASSI), image mapping spectrometry27 (IMS), and multispectral Sagnac interferometry28 (MSI). See Fig. 3 for system layout diagrams. This list of full-throughput snapshot instruments is steadily increasing, and system designers can even look forward to snapshot 3D detector arrays, in which the detector itself is capable of resolving spectra at individual pixels.29–33 Fig. 3System architectures for CTIS, CASSI, IMS, IFS-L, fiber-reformatting imaging spectroscopy (FRIS), and filter stack spectral decomposition (FSSD). 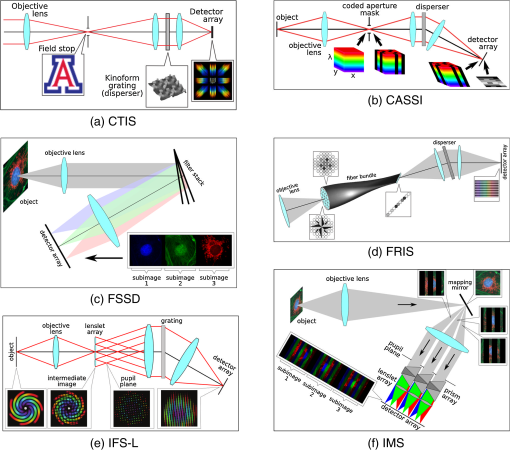 The convergence of three recent technological advances has made snapshot imaging spectrometry possible. First is the steady decrease in cost and pixel size for large format detector arrays. These enable compact instruments with a large number of sensing elements with fast readout speed and reasonable cost. Since typical datacubes have 10 million or more elements, snapshot techniques require very large detector arrays in order to properly sample a sufficient number of datacube voxels. Only in the past decade have such detector arrays become economical. The second technological advance is in the manufacturing tools for making precision multiaperture optical elements, such as lenslet and micromirror arrays. These array optical elements allow one to design compact instruments containing a large number (up to tens of thousands) of parallel optical systems. Finally, the third technological advance, the increased computing power available to desktop computers, has enabled algorithms that can readily display and analyze the large datasets produced by these instruments. 3.Measurements Where the Snapshot Advantage AppliesThe values for geometric light collection efficiency relate directly to signal collection in passive measurement situations (e.g., remote sensing), in which the user has no control over the illumination source. For active illumination systems such as microscopes, however, one can compensate for a low geometric efficiency by illuminating individual pixels of the object with high intensity laser light, and measuring with a whiskbroom spectrometer. This is the method used by confocal laser scanning microscopy (CLSM). Using coherent sources to boost the illumination power density, however, faces a fundamental limit when the power becomes high enough to alter or damage the sample, or, as in fluorescence microscopy, when all fluorophores in the illuminated region have been boosted to their excited state—a situation which is largely achieved in modern confocal laser scanning microscopes.34 At this point nothing further can be done on the illumination-side to increase light collection, placing a fundamental limit on overall signal. This is exactly what we have shown in a recent experiment: while the excitation laser of a CLSM excited the sample to 0.56 of the theoretical limit, the overall photon collection of the CLSM remained two orders of magnitude lower than that of an equivalent snapshot spectral imaging system, despite the use of a light source with four orders of magnitude lower power density.34 An active illumination setup also allows one to encode spectral information into the illumination-side, so that the detection system need not spectrally resolve the image in order to obtain the datacube measurement. At this point, however, we are not aware of a technique allowing this to be done without throughput loss. Rather, all techniques appear to involve either scanning35 or the illumination-side equivalent of the DoAp/DoFP configurations,36 so that the overall light collection suffers by a factor of or in comparison to snapshot imaging spectrometers using broadband illumination. For remote sensing, on the other hand, the geometric light collection efficiency is all-important. Here the user does not have the ability to manipulate the light source, and almost all object datacube voxels are continuously emitting light, so that only a parallel light collection technique can capture the full signal. For scanning instruments, this setup results in a tradeoff between light efficiency and the number of scan elements, a feature which has frustrated the expansion of imaging spectrometry into new fields where there is just not enough light to permit a tradeoff. These include, for example, spectral imaging of dynamic objects, target tracking,37 and overcoming signal-to-noise-ratio-limited spectral unmixing.38–40 The full-throughput snapshot advantage does, however, come at the price of an increase in system complexity, either in the optical hardware or in the reconstruction software. Most of the snapshot techniques involve arrays of optical elements, and thus require advanced manufacturing techniques that have only recently become available. In addition, with the exception of CASSI, all of these instruments require large format detector arrays, and this is perhaps their primary limitation. Detector technology, however, has been advancing at a pace paralleling that of Moore’s law,41,42 so that we can expect these limitations to ease in the coming years, both in terms of the overall pixel count, cost per pixel, and pixel readout speed. One may argue that the complexity tradeoff compromises the snapshot advantage. The division of aperture technique, for example, consists of an array of mini-cameras each with its own spectral filter. For an array of 25 cameras [as shown in Fig. 2(a)], the system pupil is 25 times as large as the pupil of each individual camera. Thus, if we compare a full-throughput technique with a DoAp, we can say that the simplicity of the DoAp should allow one to implement a larger pupil than the snapshot technique can, and this should improve light collection. A similar argument holds for the multispectral filter array camera: using focal plane division techniques allows one to use front end optics with lower resolution than a comparable snapshot system, and this resolution change can be achieved simply by increasing the pupil diameter, which improves on light collection.* In practice, however, the tradeoff between complexity and light collection has not significantly impacted instruments presented within the journal literature: the DoAp and DoFP approaches so far constructed (see Refs. 14, 16, and 19) do not show an order of magnitude larger pupil diameters than their full-throughput counterparts have been able to achieve (see Ref. 27). Note that although CASSI, IRIS, and MSI all suffer from a 50% efficiency loss (the first due to the use of a binary mask, the others due to the need to polarize incoming light), these are still labeled as “full-throughput” techniques because the factor of two in light lost will be much lower than the factor of advantage due to snapshot collection. CTIS also suffers from significant light loss due to inefficiencies in grating dispersion into the designed diffractive orders, but this factor will also generally be small in comparison to . Finally, while one advantage of snapshot instruments is the absence of scanning artifacts when imaging moving objects, this does not imply that one obtains the full data in real time. Both CTIS and CASSI are computationally intensive instruments, and this can create a considerable delay between raw data acquisition and the final delivery of the datacube. An overview of the various snapshot instruments and their maximum theoretical efficiency values are given in Table 1. Table 1Snapshot instruments and their maximum theoretical efficiency values.
4.Snapshot High-D SystemsThe snapshot advantage in imaging spectrometry is a direct analogue of the advantage of staring versus scanning infrared imagers demonstrated during the 1980s and 1990s.44–47 Scanning infrared imaging systems used single-point detectors scanned in two dimensions across a scene, or a linear array of detector elements scanned across one dimension of the scene, in order to obtain a complete 2D image. Scanning systems suffered an efficiency loss equal to the number of elements in the scan dimension as a direct result of using a lower-dimensional detector array (single detector or 1D array) to measure a higher-dimensional dataset, the 2D image. This is equivalent to the imaging spectrometer problem of detecting a 3D dataset on a lower-dimensional 2D detector array. While infrared detectors evolved to allow detectors whose dimensionality matched the measurement data (2D for an image), the only way for an imaging spectrometer to avoid scanning is to design an optical system in which the light distribution on the 2D detector array encodes the full three-dimensional distribution of light within the object’s datacube. Doing this encoding without sacrificing light achieves the snapshot advantage. The concept of a snapshot advantage also extends beyond just imaging spectrometry. It applies equally well to any high-dimensional (high-D) system—an instrument whose data dimensionality is higher than just the two dimensions available for detector arrays. The plenoptic function describes the complete distribution of data obtainable from passively sampling the optical field,48 and thus describes the highest data dimensionality to which we have ready access via optics. (Here and describe the polarization and time variation of the optical field.†) Since higher-dimensional measurement systems parcel the finite number of photons collected into ever smaller bins, maintaining snapshot capability becomes important for anything beyond the measurement of static objects in a laboratory setting. The “light field camera,” for example, is a snapshot instrument which collects angularly resolved image data by re-mapping the 4D distribution onto a two-dimensional detector array.49 A similar but much less compact implementation uses an array of individual cameras.50 These snapshot aprroaches thus have a throughput advantage over any system which scans over angle in order to obtain the full dataset.‡ This is separate from the reduced signal-to-noise ratio in each data element due to the use of smaller bins that come with higher dimensionality measurement. Snapshot techniques thus become increasingly important with increasing dimensionality, with the tradeoff that much larger detector arrays are needed to accommodate the larger datasets. Other examples of snapshot high-D systems include channeled imaging polarimeters,51–53 which measure an dataset; line imaging spectropolarimeters54,55 which measure ; and computed tomographic imaging channeled spectropolarimeters56,57 (CTICS), which measure . For polarization systems, the snapshot advantage in light efficiency is limited, since the theoretical maximum efficiency improvement over a scanning system is only 4 (for a Stokes polarimeter) or 16 (for a Mueller matrix polarimeter). Since polarimetry typically requires computational reconstruction of the data, the need for accurate calibration58 means that snapshot systems’ lack of moving parts is usually the more important feature. 5.ConclusionWhen measuring high-D data, full-throughput snapshot instruments have a light collection capacity which exceeds that of all scanning and all throughput-division snapshot instruments by a simple geometric factor which we call the snapshot advantage. Any experimental setup whose measurement dimensionality exceeds that of the detector, and in which all data elements (e.g., datacube voxels in imaging spectrometry) are luminous throughout the measurement period can use this advantage fully. While there currently exist only a handful of instruments capable of full-throughput snapshot measurements of 3D or 4D data, we expect to see more as researchers find new ways of adapting new technology to these challenging measurements. Since the full-throughput snapshot techniques map each element in the data to an individual pixel, the primary limitation to constructing snapshot versions of such instruments is the limited number of pixels available with current detector arrays, such that any system attempting to perform snapshot measurements beyond 4D will need to wait for the development of much larger detector arrays. At some point instrument designers may learn how to relax this “curse of dimensionality”59 by taking advantage of ideas such as compressive sensing,60 but we have not yet learned to do this while maintaining data fidelity. Notes*Since cameras are more often than not operated in the aberration-limited regime rather than diffraction-limited, increasing the pupil size results in increased aberrations and loss of resolution. †Since s is restricted to a discrete space of only a few elements (with the exact number of elements depending on one’s choice of polarization representation) it is arguably not a “dimension,” or, at least, not a dimension of the same nature of the remaining seven elements of the plenoptic function. ‡The size of the dataset delivered by this instrument illustrates some of the complexity tradeoff for full-throughput snapshot measurement. By sampling in angle over a (Nθx,Nθy)=(14,14) domain, the number of detector pixels required increases by 142=196. Obtaining megapixel spatial sampling in a snapshot is thus unobtainable with all but the largest mosaicked detector arrays available today. AcknowledgmentsThis work was partially supported by National Institutes of Health (NIH) Grants RO1-CA124319 and R21-EB009186. References
“Landsat 7 science data users handbook,”
(2011). https://doi.org/http://landsathandbook.gsfc.nasa.gov/. Google Scholar
R. O. Greenet al.,
“Imaging spectroscopy and the airborne visible/infrared imaging spectrometer (AVIRIS),”
Rem. Sens. Environ., 65
(2), 227
–248
(1998). http://dx.doi.org/10.1016/S0034-4257(98)00064-9 RSEEA7 0034-4257 Google Scholar
N. Gat,
“Imaging spectroscopy using tunable filters: a review,”
Proc. SPIE, 4056 50
–64
(2000). http://dx.doi.org/10.1117/12.381686 Google Scholar
L. W. SchumannT. S. Lomheim,
“Infrared hyperspectral imaging fourier transform and dispersive spectrometers: comparison of signal-to-noise based performance,”
Proc. SPIE, 4480 1
–14
(2002). http://dx.doi.org/10.1117/12.453326 PSISDG 0277-786X Google Scholar
A. Barducciet al.,
“Theoretical aspects of Fourier transform spectrometry and common path triangular interferometers,”
Opt. Express, 18
(11), 11622
–11649
(2010). http://dx.doi.org/10.1364/OE.18.011622 OPEXFF 1094-4087 Google Scholar
M. DescourE. Dereniak,
“Computed-tomography imaging spectrometer: experimental calibration and reconstruction results,”
Appl. Opt., 34
(22), 4817
–4826
(1995). http://dx.doi.org/10.1364/AO.34.004817 APOPAI 0003-6935 Google Scholar
R. Content,
“A new design for integral field spectroscopy with 8-m telescopes,”
Proc. SPIE, 2871 1295
–1305
(1997). http://dx.doi.org/10.1117/12.269020 PSISDG 0277-786X Google Scholar
R. Baconet al.,
“The SAURON project — the panoramic integral-field spectrograph,”
Mon. Not. Roy. Ast. Soc., 326
(1), 23
–35
(2001). http://dx.doi.org/10.1046/j.1365-8711.2001.04612.x Google Scholar
M. A. Bershady,
“3D spectroscopic instrumentation,”
XVII Canary Island Winter School of Astrophysics, Cambridge University Press(2009). Google Scholar
A. R. Harveyet al.,
“Technology options for imaging spectrometry,”
Proc. SPIE, 4132 13
–24
(2000). http://dx.doi.org/10.1117/12.406592 Google Scholar
A. R. HarveyD. W. Fletcher-Holmes,
“High-throughput snapshot spectral imaging in two dimensions,”
Proc. SPIE, 4959 46
–54
(2003). http://dx.doi.org/10.1117/12.485557 PSISDG 0277-786X Google Scholar
R. G. SellarG. D. Boreman,
“Comparison of relative signal-to-noise ratios of different classes of imaging spectrometer,”
Appl. Opt., 44
(9), 1614
–1624
(2005). http://dx.doi.org/10.1364/AO.44.001614 APOPAI 0003-6935 Google Scholar
H. R. MorrisC. C. HoytP. J. Treado,
“Imaging spectrometers for fluorescence and Raman microscopy: acousto-optic and liquid crystal tunable filters,”
Appl. Spectros., 48
(7), 857
–866
(1994). http://dx.doi.org/10.1366/0003702944029820 APSPA4 0003-7028 Google Scholar
T. InoueK. Itoh,
“Fourier-transform spectral imaging near the image plane,”
Opt. Lett., 16
(12), 934
–936
(1991). http://dx.doi.org/10.1364/OL.16.000934 OPLEDP 0146-9592 Google Scholar
K. Itoh,
“Interferometric multispectral imaging,”
Progr. Opt., 35 145
–196
(1996). http://dx.doi.org/10.1016/S0079-6638(08)70529-8 POPTAN 0079-6638 Google Scholar
S. A. Mathews,
“Design and fabrication of a low-cost, multispectral imaging system,”
Appl. Opt., 47
(28), F71
–F76
(2008). http://dx.doi.org/10.1364/AO.47.000F71 APOPAI 0003-6935 Google Scholar
N. GuptaP. R. AsheS. Tan,
“Miniature snapshot multispectral imager,”
Opt. Eng., 50
(3), 033203
(2011). http://dx.doi.org/10.1117/1.3552665 OPENEI 0892-354X Google Scholar
L. MiaoH. QiW. Snyder,
“A generic method for generating multispectral filter arrays,”
in Int. Conf. Image Process,
3343
–3346
(2004). http://dx.doi.org/10.1109/ICIP.2004.1421830 Google Scholar
J. BrauersT. Aach,
“A color filter array based multispectral camera,”
12. Workshop Farbbildverarbeitung, Ilmenau(2006). Google Scholar
M. R. Descour,
“Non-scanning imaging spectrometry,”
University of Arizona,
(1994). Google Scholar
C. Vanderriest,
“Integral field spectroscopy with optical fibers,”
3D Optical Spectroscopic Methods in Astronomy, 71 209
–218 Astron. Soc. Pac., vol. 1995). Google Scholar
D. RenJ. Allington-Smith,
“On the application of integral field unit design theory for imaging spectroscopy,”
Publ. Astron. Soc. Pac., 114
(798), 866
–878
(2002). http://dx.doi.org/10.1086/pasp.2002.114.issue-798 PASPAU 0004-6280 Google Scholar
R. Baconet al.,
“3D spectrography at high spatial resolution. I. Concept and realisation of the integral field spectrograph TIGER,”
Astron. Astrophys., 113 347
–357
(1995). AAEJAF 0004-6361 Google Scholar
L. Weitzelet al.,
“3D: the next generation near-infrared imaging spectrometer,”
Astron. Astrophys. Suppl. Series, 119 531
–546
(1996). http://dx.doi.org/10.1051/aas:1996266 AAESB9 0365-0138 Google Scholar
T. C. Georgeet al.,
“Distinguishing modes of cell death using the ImageStream multispectral imaging flow cytometer,”
Cytometry A, 59
(2), 237
–245
(2004). http://dx.doi.org/10.1002/(ISSN)1097-0320 1552-4922 Google Scholar
M. E. Gehmet al.,
“Single-shot compressive spectral imaging with a dual-disperser architecture,”
Opt. Express, 15
(21), 14,013
–14,027
(2007). http://dx.doi.org/10.1364/OE.15.014013 OPEXFF 1094-4087 Google Scholar
L. Gaoet al.,
“Snapshot image mapping spectrometer (IMS) with high sampling density for hyperspectral microscopy,”
Opt. Express, 18
(14), 14,330
–14,344
(2010). http://dx.doi.org/10.1364/OE.18.014330 OPEXFF 1094-4087 Google Scholar
M. W. Kudenovet al.,
“White-light Sagnac interferometer for snapshot multispectral imaging,”
Appl. Opt., 49
(21), 4067
–4075
(2010). http://dx.doi.org/10.1364/AO.49.004067 APOPAI 0003-6935 Google Scholar
P. Mitraet al.,
“Multispectral long-wavelength quantum-well infrared photodetectors,”
Appl. Phys. Lett., 82
(19), 3185
–3187
(2003). http://dx.doi.org/10.1063/1.1573354 APPLAB 0003-6951 Google Scholar
D. L. GilblomS. K. Yoo,
“Infrared and ultraviolet imaging with a CMOS sensor having layered photodiodes,”
Proc. SPIE, 5301 186
–192
(2004). http://dx.doi.org/10.1117/12.528427 Google Scholar
X. C. Sunet al.,
“Multispectral pixel performance using a one-dimensional photonic crystal design,”
Appl. Phys. Lett., 89
(22), 223522
(2006). http://dx.doi.org/10.1063/1.2400069 APPLAB 0003-6951 Google Scholar
P. Parreinet al.,
“Multilayer structure for a spectral imaging sensor,”
Appl. Opt., 48
(3), 653
–657
(2009). http://dx.doi.org/10.1364/AO.48.000653 APOPAI 0003-6935 Google Scholar
J. Wanget al.,
“Cavity-enhanced multispectral photodetector using phase-tuned propagation: theory and design,”
Opt. Lett., 35
(5), 742
–744
(2010). http://dx.doi.org/10.1364/OL.35.000742 OPLEDP 0146-9592 Google Scholar
L. Gaoet al.,
“Depth-resolved image mapping spectrometer (IMS) with structured illumination,”
Opt. Express, 19
(18), 17,439
–17,452
(2011). http://dx.doi.org/10.1364/OE.19.017439 OPEXFF 1094-4087 Google Scholar
M. V. SarunicS. WeinbergJ. A. Izatt,
“Full-field swept-source phase microscopy,”
Opt. Lett., 31
(10), 1462
–1464
(2006). http://dx.doi.org/10.1364/OL.31.001462 OPLEDP 0146-9592 Google Scholar
G. J. TearneyR. H. WebbB. E. Bouma,
“Spectrally encoded confocal microscopy,”
Opt. Lett., 23
(15), 1152
–1154
(1998). http://dx.doi.org/10.1364/OL.23.001152 OPLEDP 0146-9592 Google Scholar
M. V. A. MurzinaJ. P. Farrell,
“Dynamic hyperspectral imaging,”
135
–144
(2005). http://dx.doi.org/10.1117/12.598620 Google Scholar
P. GongA. Zhang,
“Noise effect on linear spectral unmixing,”
Ann. GIS, 5 52
–57
(1999). http://dx.doi.org/10.1080/10824009909480514 1947-5683 Google Scholar
A. BarducciA. Mecocci,
“Theoretical and experimental assessment of noise effects on least-squares spectral unmixing of hyperspectral images,”
Opt. Eng., 44
(8), 087008
(2005). http://dx.doi.org/10.1117/1.2010107 OPENEI 0892-354X Google Scholar
M. E. Winter,
“Error rates of unmixed hyperspectral imagery,”
Proc. SPIE, 6233 623327
(2006). http://dx.doi.org/10.1117/12.668624 Google Scholar
A. Rogalski,
“Optical detectors for focal plane arrays,”
Opto-electron. Rev., 12
(2), 221
–245
(2004). Google Scholar
A. Rogalski,
“Recent progress in infrared detector technologies,”
Infrared Phys. Tech., 54
(3), 136
–154
(2011). http://dx.doi.org/10.1016/j.infrared.2010.12.003 IPTEEY 1350-4495 Google Scholar
J. Bland-Hawthornet al.,
“Hexabundles: imaging fiber arrays for low-light astronomical applications,”
Opt. Express, 19
(3), 2649
–2661
(2011). http://dx.doi.org/10.1364/OE.19.002649 OPEXFF 1094-4087 Google Scholar
M. SchlessingerI. J. Spiro, Infrared Technology Fundamentals,
(1995). Google Scholar
O. Naveh,
“Sensitivity of scanning and staring infrared seekers for air-to-air missiles,”
Proc. SPIE, 3061 692
–711
(1997). http://dx.doi.org/10.1117/12.280389 Google Scholar
Principles of Naval Weapons Systems, Kendall Hunt, Dubuque, Iowa
(2000). Google Scholar
Night Vision Thermal Imaging Systems Performance Model: User’s Manual and Reference Guide, 5 ed.Fort Belvoir, VA, rev.2001). Google Scholar
E. H. AdelsonJ. R. Bergen,
“The plenoptic function and the elements of early vision,”
Computational Models of Visual Processing, 3
–20 MIT Press, pp. 1991). Google Scholar
R. Nget al.,
“Light field photography with a hand-held plenoptic camera,”
Tech. Rep. CTSR, 2005-02
(2005). Google Scholar
B. Wilburnet al.,
“High performance imaging using large camera arrays,”
ACM Trans. Graphics, 24
(3), 765
–776
(2005). http://dx.doi.org/10.1145/1073204 ATGRDF 0730-0301 Google Scholar
K. OkaT. Kaneko,
“Compact complete imaging polarimeter using birefringent wedge prisms,”
Opt. Express, 11
(13), 1510
–1519
(2003). http://dx.doi.org/10.1364/OE.11.001510 OPEXFF 1094-4087 Google Scholar
M. W. Kudenovet al.,
“White-light channeled imaging polarimeter using broadband polarization gratings,”
Appl. Opt., 50
(15), 2283
–2293
(2011). http://dx.doi.org/10.1364/AO.50.002283 APOPAI 0003-6935 Google Scholar
M. W. Kudenovet al.,
“Snapshot imaging Mueller matrix polarimeter using polarization gratings,”
Opt. Lett., 37
(8), 1367
–1369
(2012). OPLEDP 0146-9592 Google Scholar
C. Zhanget al.,
“A static polarization imaging spectrometer based on a Savart polariscope,”
Opt. Commun., 203
(1–2), 21
–26
(2002). http://dx.doi.org/10.1016/S0030-4018(01)01726-6 OPCOB8 0030-4018 Google Scholar
S. H. JonesF. J. IannarilliP. L. Kebabian,
“Realization of quantitative-grade fieldable snapshot imaging spectropolarimeter,”
Opt. Express, 12
(26), 6559
–6573
(2004). http://dx.doi.org/10.1364/OPEX.12.006559 OPEXFF 1094-4087 Google Scholar
D. Sabatkeet al.,
“Snapshot imaging spectropolarimeter,”
Opt. Eng., 41
(7), 1048
–1054
(2002). http://dx.doi.org/10.1117/1.1467934 OPENEI 0892-354X Google Scholar
N. Hagen,
“Snapshot imaging spectropolarimetry,”
University of Arizona,
(2007). Google Scholar
J. S. Tyoet al.,
“Review of passive imaging polarimetry for remote sensing applications,”
Appl. Opt., 45
(22), 5453
–5469
(2006). http://dx.doi.org/10.1364/AO.45.005453 APOPAI 0003-6935 Google Scholar
D. L. Donoho,
“High-dimensional data analysis: the curses and blessings of dimensionality,”
American Math. Society Lecture—Math Challenges of the,
(2000). Google Scholar
E. J. CandèsM. B. Wakin,
“An introduction to compressive sampling,”
IEEE Signal Process. Mag., 25
(2), 21
–30
(2008). http://dx.doi.org/10.1109/MSP.2007.914731 ISPRE6 1053-5888 Google Scholar
Biography Nathan Hagen worked for Thermawave (now KLA Tencor) from 1996 to 2002, as a member of the R&D team developing optical metrology instruments. He graduated with a PhD degree in optical sciences at the University of Arizona in 2007, studying snapshot imaging spectrometry and spectropolarimetry (including CTIS and CTICS). From 2007 to 2009, he worked as a postdoc at Duke University, developing imaging and spectrometry techniques (including CASSI). He joined Rice University as a research scientist in 2009, where he joined the effort to develop the IMS imaging spectrometer, and to continue developing new imaging and spectrometry techniques.  Robert Kester is the chief technology officer and co-founder of Rebellion Photonics. He is also a co-inventor of the image mapping spectrometer (IMS) technology being commercialized by Rebellion Photonics and has extensive experience designing, fabricating, and testing optical devices. He has 10+ years of optics related experience and currently has 8 peer-reviewed publications and 2 pending patents. He has a MSc from the College of Optical Sciences, University of Arizona, Tucson, AZ and a PhD in Bioengineering from Rice University, Houston, TX.  Liang Gao received his BS degree in physics at Tsinghua University in 2005 and his PhD degree in applied physics at Rice University in 2011. He is currently a postdoctoral research associate in bioengineering at Rice University, Houston, Texas, in the laboratory of Tomasz Tkaczyk. His research interests include microscopy, optical design and fabrication, and biomedical imaging.  Tomasz S. Tkaczyk is an assistant professor of bioengineering and electrical and computer engineering at Rice University, Houston, Texas, where he develops modern optical instrumentation for biological and medical applications. His primary research is in microscopy, including endoscopy, cost-effective high-performance optics for diagnostics, and multidimensional snapshot imaging systems. He received his MS and PhD degrees from the Institute of Micromechanics and Photonics, department of Mechatronics, Warsaw University of Technology, Poland. Beginning in 2003, after his postdoctoral training, he worked as a research professor at the College of Optical Sciences, University of Arizona. He joined Rice University in the summer of 2007. |


