|
|
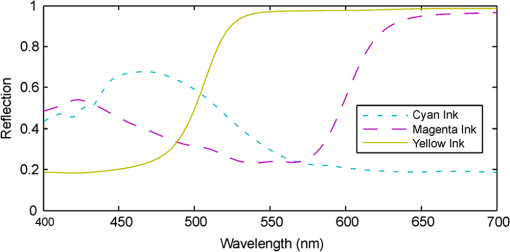
1.IntroductionThe anaglyph three-dimensional (3D) method is the most commonly used technique for printing stereoscopic 3D images, with it being used in a wide range of technical and entertainment publications. The anaglyph technique uses spectral multiplexing to encode left and right views within a single printed image. The left and right perspective images are encoded in complementary color channels of the image–usually the left image in the red channel and the right image in the blue and green color channels. To see the anaglyph 3D image, the observer wears a pair of glasses fitted with color filters in front of each eye—usually red for the left eye and cyan (blue plus green) for the right eye. The color filters act to separate the components of the presented anaglyph 3D image with the aim that the left-perspective image is only seen by the left eye, and the right-perspective image is only seen by the right eye, and allow the observer to see a compelling stereoscopic 3D image. There are many techniques which can be used to print 3D images1 (e.g., lenticular, free-view stereo-pairs, stereo-pairs viewed with mirror or lensed viewers, parallax barrier, polarized vectographs,2 and polarized StereoJet prints2), however anaglyph printing is the most commonly used 3D printing technique, primarily because of its economy and ease of use. Despite its popularity, anaglyph 3D printing suffers from probably the lowest 3D quality of all the 3D printing methods. Given the continued widespread use of the anaglyph 3D technique, there is value in efforts to improve the image quality of this technique. Anaglyph 3D has several limitations in terms of the quality of the presented 3D images—particularly the inability to produce accurate full-color 3D images (since color is used as the separation or multiplexing technique), binocular rivalry3 (sometimes known as retinal rivalry) (because each eye sees a different color), and often the presence of high levels of crosstalk.4 This paper concentrates on the 3D image quality metric of crosstalk, which can be defined as the “incomplete isolation of the left and right image channels”5,6 such that one eye can see a ghost image from the other channel. Crosstalk is one of the main determinants of 3D image quality7 and stereoscopic viewing comfort.8 Although there is very little literature on the perceptual effects of crosstalk in anaglyph 3D images, there is a good body of work on the perceptual effects of crosstalk in other stereoscopic 3D display technologies. Crosstalk has been found to “strongly affect subjective ratings of display image quality and visual comfort” in an active shutter stereoscopic display,9 “significantly degrade viewing comfort” in a polarized projected 3D display,8 and have “a detrimental effect on the perceived magnitude of depth from disparity and monocular occlusions” using a mirror-stereoscope display.10 Studies have found crosstalk levels of 5% to 9% can significantly affect visual comfort and image quality.8,9 Our own anecdotal evidence indicates that anaglyph 3D images are similarly adversely affected by crosstalk. Several methods have been proposed for improving the perceived quality of anaglyph 3D images: applying crosstalk cancellation to reduce the perception of ghosting due to crosstalk,11 registering the parallax of foreground objects,12 using different primary color combinations,13 and using different anaglyph multiplexing algorithms to calculate the RGB values of the anaglyph image.14–20 The choice of anaglyph multiplexing algorithm will determine the amount and quality of color reproduction in the anaglyph image and inversely, the amount of binocular rivalry. For example, a highly saturated scene can cause high levels of binocular rivalry if a high color reproduction anaglyph algorithm is used. However, binocular rivalry can be reduced by using an anaglyph algorithm which desaturates the input images, but this reduces the quality of color reproduction.20 This paper uses the technique of optimizing the spectral curves of the “display” and glasses, and maintaining purity of the color channels, as a way of reducing anaglyph crosstalk,4,21 which is different but complementary to the improvement techniques listed above. In the context of printed anaglyphs discussed in this paper, the term “display” will be used to refer to the printed image which is displayed to the observer—and indirectly the specific ink set and paper used to generate the print, and the light source used to illuminate it. The anaglyph 3D technique dates back to 1853 when it was developed by William Rollman22—although it is believed he only used solid blocks of color in his work and not continuous tone images. Louis Ducos Duhauron is credited as inventing the continuous tone printed anaglyph in 1891.23–25 In 1895, Alfred Watch26 presented a descriptive article introducing the printed anaglyph process. Despite anaglyph 3D prints having been with us for over a hundred years, it is surprising that there have been relatively few technical publications to have described the science and technique of the printed anaglyph 3D image over this period, and several fundamental problems remain unsolved. In 1937, John Norling27 identified that “inks, pigments and dyes commonly used in printing the red and blue pictures are not pure colors” and hence “a residual image or ghost image” will be present, and patented a technique of overprinting with yellow ink to improve the printed spectra. In 2002, Steven Harrington et al.28,29 disclosed a series of work on Illuminant Multiplexed Images, encoding separate images in the separate ink colors, and decoding the images using narrow-band light sources. This topic has some relevance to anaglyph imaging however their work did not specifically address printed anaglyphs viewed through anaglyph glasses. In 2005, Vu Tran18 described the development of an anaglyph multiplexing algorithm for printed anaglyphs which aimed to improve the color rendition of printed anaglyphs (using dichopic color mixture theory)18 and reduce crosstalk. In this dissertation, he identified that in-built color management can disrupt the quality of printed anaglyphs (which agrees with our findings) and developed a detailed algorithm to cope with this effect. He also wrote “the illuminant light does not have a strong effect on overall 3D perception” which disagrees with our findings. In 2011, Ru Zhu Zeng19 described another algorithm to color correct anaglyph 3D images for printing, but the paper did not disclose the details. In 2009, Ron Labbe1 provided a summary of 3D printing techniques and a timeline of the use of the printed anaglyph in publicly released publications. He also correctly identified that “the inks in the CMYK process do not lend themselves to a perfectly ghost-free image, especially the cyan”1—this is discussed in further detail later in Sec. 5.3. Moving on from the traditional printed anaglyph, in 1974 Jay Scarpetti30 proposed a printed anaglyph technique based on a front and back lit printed transparency, and in 2009, Monte Ramstad31 disclosed an extension of the conventional anaglyph printing process using fluorescent inks, but these techniques do not offer any direct benefit to the conventional printed anaglyph. Attempts to optimize the performance of printed anaglyph images by the appropriate choice of printing inks and filters in the anaglyph glasses has also been performed for some time but mainly in an empirical manner.32,33 This paper proposes a similar optimization, but using a technical analysis and simulation to guide the choice of glasses and inks, with an additional variable which is the choice of light source. The work on printed anaglyphs described in this paper builds upon previous work that some of the authors of this paper published on crosstalk with anaglyph images on emissive displays such as liquid crystal displays (LCDs), plasma display panels (PDPs), digital light projection televisions (DLP TVs) and cathode ray tubes (CRTs).4,13,21,34 Emissive displays and printed images differ in the way that the image and color is generated. Emissive displays use the additive color model (by additive mixing of red, green and blue color primaries) whereas printing uses the subtractive color model (by subtractive mixing of cyan, magenta and yellow inks).35 Figure 1 provides an illustration of the difference between the additive color and subtractive color models. With an emissive display, the screen starts from a black base and then red, green or blue light is added in various combinations to produce a wide range of colors. For example, when red and blue light are added together [Fig. 1(a)] the result is a magenta color, and when red, green, and blue light are used together (in an appropriate balance), the additive result is white. In contrast to emissive displays, the starting point with color printing is a blank white page. The most commonly used primary color inks are cyan, magenta and yellow—commonly called “process inks.”35 With reference to Fig. 2, it can be seen that the yellow ink mostly attenuates (subtracts) light in the blue spectral region ( to 500 nm) whilst not substantially attenuating light in the green ( to ) and red ( to ) regions. Ideally the magenta ink attenuates (subtracts) light in the green spectral region, and cyan ink attenuates (subtracts) light in the red spectral region, while not attenuating light outside these regions. In printing, the application of cyan ink attenuates the red spectral band so it can be thought of as “minus-red,” and similarly magenta ink can be thought of as “minus-green,” and yellow ink as “minus-blue.” The combined printing of the three printing inks (cyan, magenta and yellow) in varying density allows a wide range (gamut) of colors to be presented. For example, when cyan and magenta inks are printed together [Fig. 1(b)], a blue color is generated. When ideal cyan, magenta and yellow inks are printed together, all light reflected off the white page is absorbed and a black area is created. This description serves to illustrate that the process of generating printed anaglyph 3D images is similar but has notable differences to anaglyph images on emissive displays, and these differences mean that the analysis and optimization of printed anaglyphs need to be different. Fig. 1An illustration of (a) the additive color model as used in emissive displays with red, green and blue color primaries, and (b) the subtractive color model as used in printing with cyan, magenta, and yellow color primaries. The combination of the different color primaries in varying amounts in the two models results in a wide range of possible colors. 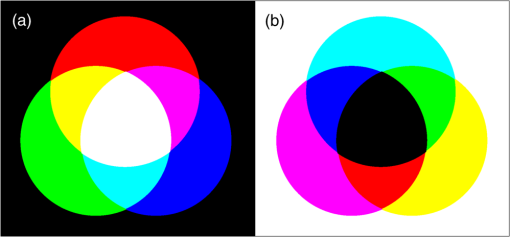 The body of this paper starts by providing a summary of the mechanisms by which crosstalk occurs in printed anaglyph 3D images. This is followed by the introduction of a mathematical model that describes and predicts the occurrence of printed anaglyph 3D crosstalk due to spectral characteristics. Next, the paper describes a visual validation experiment that was conducted to determine the accuracy of the developed model. In the discussion, the paper describes the advantages that the availability of an accurate crosstalk simulation model affords, and uses the model to investigate three methods of reducing crosstalk in anaglyph 3D prints, one of which on its own could significantly reduce anaglyph crosstalk. 2.Sources of Crosstalk in Printed AnaglyphsThis work has identified four main contributors to crosstalk in printed anaglyph images: 2.1.Spectral CharacteristicsSince the anaglyph 3D process uses spectral multiplexing to separate the left and right image channels, the spectral characteristics of the lighting, paper, printing inks and 3D glasses and how they interact will determine how light from the left and right image channels will reach the left and right eyes. The specific spectral width and cut-off wavelength of each of the printing inks in relation to the cut-off wavelength of the color filters in the anaglyph glasses will affect how well the color channels are isolated, and therefore the amount of crosstalk present. Ideally each of the cyan, magenta, and yellow inks will strongly attenuate light in the red, green, and blue color bands, respectively, while leaving the other color bands unattenuated, but in reality, the printing inks deviate from this ideal response considerably and, for example, cyan ink commonly attenuates a considerable amount of the green and blue light bands. This nonideal spectral response of the printing inks, as illustrated in Fig. 2, limits the ability to maintain isolation between the color channels and hence is another source of crosstalk. The spectral characteristics of the specific blank “white” paper used to print anaglyph 3D images can also affect anaglyph crosstalk, but in normal circumstances we expect this to be a small effect. We have also found that the spectral characteristics of the lighting used to illuminate the printed anaglyph can affect the amount of crosstalk present. The smart choice of lighting, printing inks and 3D glasses can reduce the presence of anaglyph crosstalk and this will be explored further in Sec. 3 by the use of the simulation model. 2.2.Color Space ConversionMost image editing is conducted in the RGB (red-green-blue) color space, because this is the color space needed for most emissive displays, however for printing, images must be converted to the CMYK (cyan-magenta-yellow-black) color space. When working with anaglyph images, ideally the color channels of the image will be maintained separate through the entire imaging chain, but the default RGB to CMYK color space conversion process used by most software will often mix the color channels in order to maintain color accuracy (see also Sec. 2.3.). Optimally the (red) channel (of the RGB color space) will be mapped to the (cyan) channel (of the CMYK color space), (green) to (magenta), and (blue) to (yellow), however this is often not the way the conversion is performed. If some mixing of the color channels occurs during the color space conversion, this will contribute to crosstalk. 2.3.Color ManagementColor management is a mathematical process that attempts to ensure that when an image is printed or displayed on different devices that the colors of the image appear the same between all of those devices.35 Many readers will be familiar with the situation where an image displayed on the screen of their computer can look substantially different from the same image printed using their desktop printer. Color management attempts to solve these color consistency problems by a process of characterizing and calibrating the color characteristics of the devices used to capture, present and print color images.35 In summary, each device used to capture, display or print color images needs to be characterized and a profile [often known as an International Color Consortium (ICC) profile] will be defined for each device. When a color image is transferred from one device to another, the ICC profile is used by the color management module (CMM) to “convert” the color values of the image so that the colors will look the same on the target device as they do on the source device. The process of color management usually achieves its task by mixing the color channels of the color image to achieve the desired colors—much like a painter mixes inks to achieve a desired color. This process can produce very pleasing color accurate images when used for regular two-dimensional color images; however, it is our proposition that this mixing is detrimental when applied to anaglyph 3D images and will lead to the presence of crosstalk. Although color management still has some importance with anaglyph images, the color spectrum received by each eye is distorted by the anaglyph glasses worn by the observer (which are designed to de-multiplex the different color bands to each eye) and hence the perception of color is substantially biased. The color channel mixing process used by color management also conflicts with the need to maintain isolation between the color channels in anaglyph images. We therefore suggest that there needs to be a different color management process for anaglyph images, one that maintains isolation between the color channels, perhaps by integrating the color management and color multiplexing steps into a single process.15,18 For the purposes of this project it would have been helpful if color management could be totally disabled, but we were unable to find a reliable way of achieving this with common desktop printers. Even programs which purported to offer an option to disable color management, did not actually disable color management fully. We only found one reference to a printer driver which allowed direct control of the individual inks,36 however we did not have access to this driver during the work of this paper. Interestingly, anaglyph images presented on emissive displays connected to a computer ordinarily do not suffer from any anaglyph image degradation due to color management, because many image editing applications simply directly map the RGB values of each pixel in the image to the pixels on the display without any color management. On the other hand, more advanced image editing programs may include color management and hence may introduce problems for anaglyph images. In offset printing it is possible to bypass color management because the individual separations (individual color plates for each ink color) can be controlled separately and hence avoid crosstalk caused by color management—unfortunately desktop printers do not operate using separations. 2.4.Gray Component ReplacementAlthough we referred earlier to printing commonly using only three primary inks to produce a full-color image, a fourth printing ink, black, is usually used to improve the contrast range of printed images. The problem is that the combination of real cyan, magenta and yellow inks usually produces a dark muddy brown rather than a deep black, so it is beneficial to use black ink in dark areas to improve the image quality in dark regions of the image.29,35 Black ink also has the advantage that it is cheaper than color inks so there is a financial incentive to use black ink in preference to heavy concentrations of cyan, magenta and yellow inks. Black ink can also be used in mid-gray areas of the image instead of using a combination of cyan, magenta and yellow inks. “The two basic black generation strategies are Under Color Removal (UCR), and Gray Component Replacement (GCR). UCR separations use black only in the neutral and near-neutral areas, while GCR is a more aggressive strategy that replaces the amount of CMY that would produce a neutral with , even in colors that are quite a long way from neutral.”35 If an aggressive amount of GCR is used, it can compromise the separation between the left and right image channels in near-neutral gray areas of the image and hence cause crosstalk. It is also our experience that even small amounts of black ink replacement can compromise anaglyph images, even if the black ink is only used in very dark parts of the image, for two reasons. First, the black ink is often used to expand the dark range of the image into areas of darkness that the individual color inks are not able to achieve on their own, and when viewed through anaglyph glasses this transition from a color ink area to a black ink replacement area may be noticeable, and because the introduction of black replacement can be triggered by the image content in the other perspective image channel, it can lead to crosstalk (in dark areas of the image). Second, the black ink can look quite different to equivalent density of the color primary inks when viewed through the anaglyph glasses due to subtle differences in the spectral curves of the black and color inks, which in turn can also lead to crosstalk. Our experience to date suggests that less crosstalk will be observed in printed anaglyph images if GCR and UCR can be switched off. Unfortunately we were unable to find a reliable way of disabling GCR and UCR on the color inkjet and color laser printers that we tested. 3.Simulation of Spectral CrosstalkWe have developed a crosstalk simulation model to predict the occurrence of crosstalk in printed anaglyph images due to the spectral properties of the light source, paper, inks and anaglyph glasses. The simulation used in this study builds on the crosstalk model for anaglyph images on emissive displays developed by the authors and earlier collaborators.4,13,21,34 The analysis in this paper is performed for the red/cyan color combination, but it could equally be applied to other color combinations.13 The printed anaglyph crosstalk simulation algorithm is illustrated in Fig. 3 for the example case of a red-left/cyan-right anaglyph. With reference to Fig. 3, the model uses (a) the emission spectrum of the light source (in this example an incandescent lamp), (b) the spectrum of the blank paper, (c) the spectrum of the “red” and cyan inks, (d) the spectrum of the red and cyan filters of the glasses, and (e) the human eye spectral sensitivity. Fig. 3Illustration of the process of printed anaglyph crosstalk simulation described in this paper. Each spectral graph shows wavelength on the horizontal axis (400 to 700 nm, , , ) and intensity on the vertical axis. 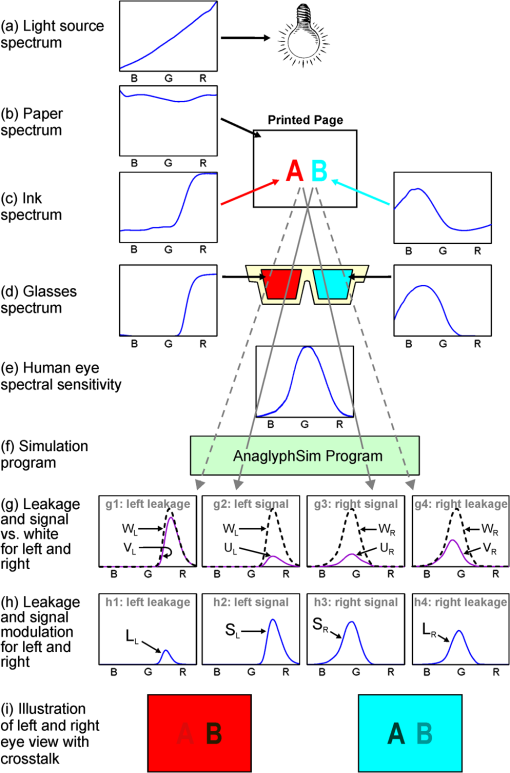 In this particular study we chose to simplify the analysis by considering the use of red ink (which is the combination of yellow and magenta inks) for the right eye channel rather than presenting the performance of yellow and magenta inks separately. It should be noted that an actual red ink is not usually available in many printers and instead it is produced by combining yellow and magenta inks. The simulation can calculate the performance of yellow and magenta inks separately but we are only reporting the results of “red” ink performance here. The anaglyph crosstalk simulation program [see Fig. 3(f)] multiplies the spectra [(a) through (e)] together to obtain the spectral plots shown in Fig. 3(g). In the four plots [Fig. 3(g1)) through 3(g4)], the dashed black line represents the luminance spectrum that is visible when the blank white page is viewed through the left or right colored lens, and the solid line represents the spectrum visible when the “red” or cyan inks are printed on the page and viewed through the left or right lenses of the glasses. Specifically, the black dashed lines shown in Fig. 3(g1) and 3(g2) are identical and show the luminance spectrum when the white page is viewed through the red lens of the glasses, and the black dashed line shown in Fig. 3(g3) and 3(g4) are identical and show the luminance spectrum when the white page is viewed through the cyan lens. The solid curves of Fig. 3(g) represent the luminance spectrum of: (g1) the “red” ink viewed through the red lens, (g2) the cyan ink viewed through the red lens, (g3) the “red” ink viewed through the cyan lens, and (g4) the cyan ink viewed through the cyan lens. The difference between the dashed and solid curves in each of these plots (g1) through (g4) represent how well each ink modulates that particular eye color channel. For example, in Fig 3(g2) there is a big gap between the dashed and solid curves which means that when cyan ink is printed on a white page it will be highly visible against the blank white page when viewed through the red lens, and in Fig. 3(g1) the small difference between the dashed and solid curves means that when this particular “red” ink is printed on a white page it will be nearly invisible against the blank white page when viewed through the red lens. The spectral plots shown in Fig. 3(h) represent the difference between the dashed and solid curves shown in the spectral plots of Fig. 3(g) immediately above. These plots represent the ability of each ink to modulate the light in each eye channel—specifically, (h1) the ability of the “red” ink to modulate the red eye channel, (h2) the ability of the cyan ink to modulate the red eye channel, (h3) the ability of the “red” ink to modulate the cyan (right-eye) channel, and (h4) the ability of the cyan ink to modulate the cyan (right-eye) channel. The areas under each of these curves represent the luminance difference that each ink is able to provide for each eye channel compared to a blank white page. For example, graphs (h2) and (h3) have the largest area under the curve which further demonstrates that “red” ink should be used to modulate the cyan-eye (right-eye) channel, and cyan ink should be used to modulate the red-eye (left-eye) channel. This is equivalent to the signal component in the analysis of an emissive display.34 The areas under the curves in graphs (h1) and (h4) are equivalent to the leakage component and should ideally be small. Graph (h1) has the smallest area under the curve representing that this particular “red” ink only slightly modulates the red (left-eye) channel, which will mean that it does not produce much leakage, which is preferred. In contrast, the area under the curve in graph (h4) is relatively large [compared to the area under (h3)], representing that the cyan ink modulates the cyan (right-eye) channel by a fairly large amount, so there will be a fair amount of leakage of the left-image channel into the right-eye. The two diagrams in Fig. 3(i) provide a diagrammatic representation of how much crosstalk will be visible for the left and right eyes in this particular example. The left-eye view appears dominated by red because the white page is being viewed through the red filter, and the right-eye view has a dominant cyan color because the white page is being viewed through the cyan filter. For the left eye, the letter “B” will be highly visible (dark) against the red background because the cyan ink does a good job of extinguishing the red part of the spectrum, and the letter “A” is only faintly visible as a light red-grey because the “red” ink only lightly attenuates the red (left-eye) channel. For the right eye, the letter “A” is highly visible because the “red” ink does a good job of extinguishing the cyan part of the spectrum, and the letter “B” will appear partly visible as a medium cyan-gray because the cyan ink moderately attenuates the cyan (right-eye) channel. In the special case of printed anaglyphs it is proposed that the crosstalk percentage is calculated by dividing the leakage luminance difference [e.g., in Fig. 3(g)] by the signal luminance difference [e.g., in Fig. 3(g)] for each eye as will be set out mathematically below. The printed anaglyph crosstalk simulation algorithm can be expressed as follows in equation form. In the first instance the amount and spectrum of light which reaches the left and right eyes, through the anaglyph glasses, off the blank (white) page is calculated: Second, the amount and spectrum of light that reaches the left and right eyes through the anaglyph glasses off the red and cyan printed areas are calculated: Thirdly, the signal and leakage components are calculated: And last the crosstalk is calculated: where and are the luminance spectrum of light which reaches the left and right eyes off an unprinted blank (white) page when it is illuminated using a specified light source, and viewed through a specified pair of anaglyph glasses. is the normalized spectral emission of the light source; is the spectral reflectance of the paper; is the normalized photopic spectral sensitivity of the human visual system37,38 as illustrated in Fig. 4(g); and are the spectral transmission of the left and right eye filters of the glasses; is the light wavelength (usually expressed in nm); and describe the wavelength range—for the human eye the range of visible light sensitivity is approximately 400 to 700 nm; and are the spectral reflectance of the inks which modulate the left and right eye channels, respectively (for red-left/cyan-right anaglyphs, will be the spectrum of the cyan ink, and will be the spectrum of the “red” ink). and are the luminance spectrum of light which reaches the left and right eyes from areas that have had the desired channel ink applied to the paper when viewed through the nominated anaglyph filter for that eye; and are the luminance spectrum of light which reaches the left and right eyes from areas that have had the undesired channel ink applied to the paper when viewed through the nominated anaglyph filter for that eye; and are effectively the signal intensity for the left and right eyes, respectively (or the ability of the appropriate ink to modulate its corresponding left or right eye channel); and are effectively the leakage intensity for the left and right eyes, respectively (or the ability of the left-channel ink to modulate light in the right eye channel, and vice versa—ideally this would be low); is the crosstalk at each eye (or combined left and right eyes)—often expressed as a percentage; and Subscripts and refer to the left-eye channel and right-eye channel, respectively. In a traditional red/cyan anaglyph, will refer to the red channel and will refer to the cyan () channel, but other color variations are possible (e.g., blue/yellow or green/magenta13).Fig. 4Spectral plots of (a) the three light sources, (b) two paper stocks, (c) the “red” ink from the four tested printers, (d) the cyan ink from the four tested printers, (e) the red filter of commercial red/blue and “cellophane” glasses (six pairs), (f) the cyan or blue filter of the commercial red/blue and “cellophane” glasses (six pairs), (g) the red filter of the commercial red/cyan and “marker-pen” glasses (six pairs) with the human visual system response also indicated, and (h) the cyan filter of the commercial red/cyan and “marker-pen” glasses (six pairs) with the human visual system response also indicated. 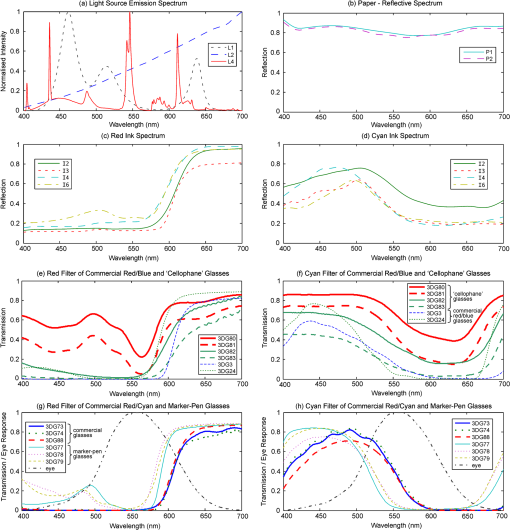 Equations (1) through (6) correspond with steps (a) through (g) in Fig. 3. Equations (7) to (10) correspond with step (h) in Fig. 3 and represent an extra step that is needed for printed anaglyphs which is not needed with anaglyphs on emissive displays. Finally Eqs. (11) through (13) calculate the amount of crosstalk present in the anaglyph printing process (for a particular light, paper, ink, glasses combination). In addition to the need for the crosstalk simulation algorithm to be an accurate portrayal of the optical processes involved, it is also important that accurate spectral data is obtained for use in the simulation—which is detailed in the next section. The anaglyph crosstalk simulation algorithm is implemented in a program we have called “AnaglyphSim” which is written in MATLAB. The program imports the spectral data for the various lights, papers, inks and glasses and implements the algorithm for the various combinations. The program calculates the percentage crosstalk and a range of other statistics for each of the combinations. It should be noted that the current simulation excludes the direct effect of GCR, color management and color space conversion, although the use of spectral data from the impure ink swatches (due to color management) in the model indirectly includes some effect of color management. Ideally, the undesirable effects of GCR, color management and color space conversion will be disabled separately and hence not need to be part of the simulation. 4.Validation of the Printed Anaglyph Crosstalk Simulation ModelThe crosstalk simulation model was validated using a four step process. 4.1.Spectral Emission of Light SourcesThe spectral emission properties of a selection of light sources were measured using an Ocean Optics USB2000 spectroradiometer. Table 1 lists the light sources used in this study. Table 1Register of light sources.
4.2.Spectral Reflectance of Papers and InksThe spectral reflectance of the papers and printing inks used in this study were measured using a PerkinElmer Lambda 35 spectrophotometer in combination with Labsphere RSA-PE-20 integrating sphere. In order to limit the number of variables in this study, a single paper type from a single batch was used throughout all the testing—a ream of “Fuji Xerox Performer+ A4” paper. Table 2 lists the four printers whose inks were tested in this study. The spectral reflectances of the inks of the various printers were obtained by printing the inks on a blank sheet of the nominated paper stock and loading them into the spectrophotometer. Each of the ink spectra was then calculated by expressing each measured ink swatch spectrum as a percentage of the spectrum of the unprinted “white” paper. Obtaining pure printed swatches of the individual inks was sometimes a difficult task. Only one of the printers that we tested (I6) was able to print a test page containing pure swatches of each ink. With the other printers it was necessary to use experimentation with various color management settings and different imaging applications to try to obtain pure test swatches, however it was not possible to obtain pure swatches using this technique and there was always some level of contamination from other inks. This contamination may not be visible to the naked eye, but can be seen with a microscope as “scum dots”35 of undesired color ink in the swatch of the desired ink color. Table 2Listing of the printers and ink sets tested.
4.3.Spectral Transmission of GlassesTwelve pairs of anaglyph glasses were used in this study—listed in Table 3. This is the same list of glasses used in the study reported in Ref. 34 except with the inclusion of two commercially manufactured red/blue anaglyph glasses (3DG3 and 3DG24) and the removal of two of the worst performing “cellophane” filter glasses (3DG84 and 3DG85). The selection of glasses consists of three red/cyan commercial pairs, two red/blue commercial pairs, three pairs constructed using marker pens, and four pairs constructed using colored “cellophane” plastic wrap. Please note that the term “cellophane” is commonly used to refer to any colored plastic wrap, however, in many countries it is a registered trademark of Innovia Films Ltd., United Kingdom. This selection of glasses provided a wide range of color filter performance which was useful for validating the crosstalk simulation model. Two pairs of red/blue anaglyph glasses were included in the set to test whether they might provide better crosstalk performance, albeit at the sacrifice of perceived color fidelity. Table 3Register of anaglyph glasses used in this study.
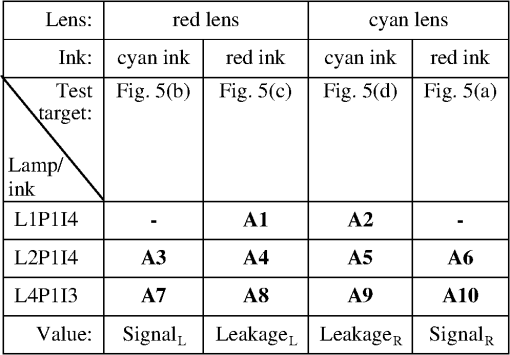
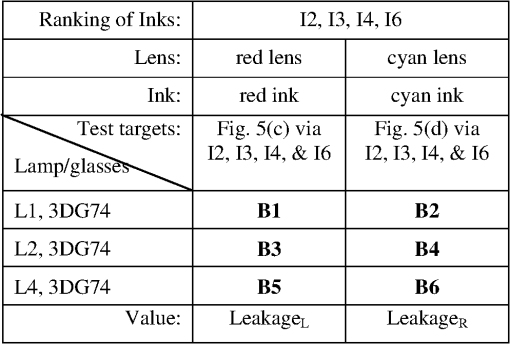
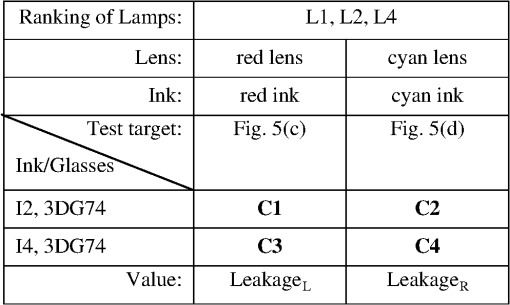
The seven pairs of hand-made glasses were constructed as previously described.34 The optical spectral transmission of the anaglyph filters were measured with a Perkin Elmer Lambda 35 spectrophotometer. It should be noted that some of the hand-made glasses have some nonideal optical properties other than their spectral transmission performance—specifically the clarity of the lens [which degrades the modulation transfer function (MTF)], dispersion, and variability of the ink density. The marker-pens tend to have a considerable amount of variability of ink density (across the filter and from filter-to-filter) due to the manual way in which the ink is applied. Glasses 3DG81 had the worst clarity of all the glasses making the image soft focused. The “Glasses IDs” used here correspond to the identification series used in previous studies.4,13,21,34 4.4.Crosstalk SimulationThe spectral data from the lights, paper, inks and glasses was processed using the anaglyph crosstalk simulation program described in Sec. 3. The simulation provides a crosstalk percentage estimate for both filters of every pair of glasses when used with every combination of light, paper and ink set. Additionally the program provides intermediate results in the calculation—namely percentage visibility of “red” ink through the red lens, percentage visibility of the cyan ink through the red lens, percentage visibility of the “red” ink through the cyan lens, and percentage visibility of the cyan ink through the cyan lens—these conditions correspond to signal and leakage (, , , and ), respectively in Fig. 3 and Eqs. (7) to (10). These four intermediate values can also be thought as the ability for each of the inks to “modulate” each of the color channels. Somewhat counter-intuitively, the “red” ink ideally only modulates the cyan color channel (while not modulating the red color channel) and cyan ink ideally only modulates the red color channel (while not modulating the cyan color channel). With the particular dataset used in this study the program calculates a total of 576 simulation result combinations (12 pairs of anaglyph glasses lenses per pair of glasses printer ink sets inks per printer (“red” and cyan) paper type ). 4.5.Visual RankingThe crosstalk performance of the various anaglyph filters were visually ranked to allow a comparison with the crosstalk simulation model results. In a previous study,34 the visual ranking was performed on the basis of the amount of crosstalk of each combination, but, it can be difficult for an observer to judge crosstalk visually because it is a derived value—that is, the luminance of the leakage component divided by the luminance of the signal component, whilst also ignoring the effect of overall luminance and any other lens effects such as defocus or filter pigment variability. For this particular project, it was decided to perform the visual ranking on the basis of a simpler intermediate value—i.e., the percentage visibility of a particular ink through a particular colored lens (i.e., modulation). This simplifies the comparison for the user, but still provides a useful ranking comparison in order to test the validity of the simulation. Figure 5 shows the four different printed test targets used to perform the visual ranking. Each of the four test targets was printed separately on each of the four printers listed in Table 2 (resulting in 16 test sheets). Figure 5(a) is used to compare the percentage visibility of the “red” ink through the cyan lens—ideally “red” ink should appear dark or black when viewed through the cyan lens. The black surround in Fig. 5(a) and 5(b) was included because it was found to make it easier to judge the darkness of the colored ink area. Figure 5(b) is used to compare the percentage visibility of the cyan ink through the red lens—ideally cyan ink should appear dark or black when viewed through the red lens. Figure 5(c) is used to compare the percentage visibility of the “red” ink through the red lens, and Fig. 5(d) is used to compare the percentage visibility of the cyan ink through the cyan lens. Fig. 5The four printed visual test targets used during the anaglyph crosstalk visual ranking tests. Target (a) was used to measure the ability of “red” ink to modulate cyan light (as viewed through the cyan lens), (b) was used to measure the ability of cyan ink to modulate red light (as viewed through the red lens), (c) was used to measure the invisibility of the “red” ink when viewed through the red lens, and (d) was used to measure the invisibility of the cyan ink when viewed through the cyan lens. The test targets are printed one per page for each printer ink set. 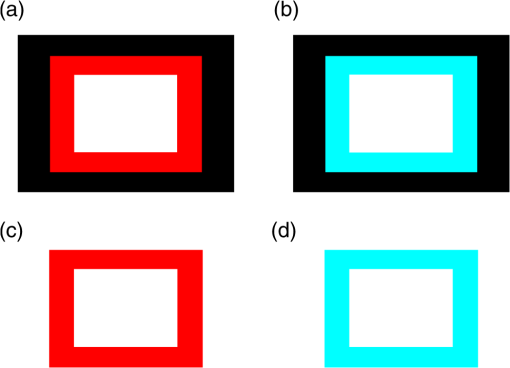 In the authors’ previous study34 of anaglyph crosstalk on emissive displays the visual ranking was performed across only a single dimension (i.e., across the 12 sets of anaglyph glasses for a particular display condition). This provided a good validation of the simulation’s ability to correctly estimate the relative performance of different sets of anaglyph glasses, however it did not specifically validate the model’s ability to correctly estimate the relative performance of different displays. In this study, the visual ranking process was expanded to include two additional conditions which ranked anaglyph performance between (a) the four different ink sets, and (b) the three different light sources—therefore the model is now being validated in three dimensions (glasses, ink set, and light source). Five observers (labeled Ob1 to Ob5) took part in the visual ranking tests. Due to the large number of individual test combinations (576 as stated in the previous section) it was necessary to limit the number of test rank combinations performed by the observers. We feel that the range of rank tests performed (detailed below) allowed a reasonable assessment, whilst also limiting the time to undertake the experiment to avoid observer overload. The visual ranking process took approximately two hours for each observer. The first test condition performed was a ranking in the glasses dimension. The 12 pairs of glasses listed in Table 3 were mounted in similar white frames, ordered randomly, and each observer was asked to rank the glasses whilst looking at a particular test target [Fig. 5(a)–5(d)] printed by a particular printer, illuminated by a nominated light source. The observers were asked to compare two glasses at a time using the printed test target and to place the glasses on the table in front of them with the lowest modulation (least visibility) on the left to the highest modulation (highest visibility) on the right. Each observer made multiple passes through the set of glasses in front of them to confirm that the glasses were in the correct order. Each observer performed a separate sorting task for each condition, so that each observer performed 10 glasses sorting tasks (labeled “A1” through “A10” in Table 4). The visual ranking test was conducted in a photographic dark room with the only source of lighting being the specified light source (from Table 1) so as to prevent ambient lighting affecting the results. The observers were briefed at the beginning of the visual trials as to the background of the project and the process they were to use in each visual rank test. Table 4Listing of the 10 glasses ranking experimental conditions conducted. For example, condition “A1” is conducted with the “red” ink test target Fig. 5(c) in the L1P1I4 display condition viewed through the red lens of the 12 pairs of glasses, which equates to a comparison of the “Left Leakage” value. (L1P1I4=Light 1 (RGB LED Lamp), Paper 1 (Fuji Xerox Performer+), Ink set 4 (Epson 835 printer)—per Tables 1 and 2). The second test condition performed was a ranking in the ink set dimension. A single pair of glasses (3DG74) was used to view and rank a set of four test prints (one from each of the four printers), whilst illuminated by a specified lamp. The six test conditions for this test are itemized in Table 5. Each observer was asked to rank the four test prints in terms of the amount of leakage each condition exhibited. Table 5Listing of the six printer ink set ranking experimental conditions. For example, condition “B1” is conducted with four printed test targets version Fig. 5(c) printed on each of the four printers with the “red” ink, illuminated by the RGB LED lamp (lamp 1) and viewed through the red lens of glasses 3DG74, which equates to a comparison of the “Left Leakage” value. (The meanings of L#, I# and 3DG# are itemized in Tables 1–3, respectively). The third test condition performed was a ranking in the lamp illuminant dimension. A single pair of glasses (3DG74), was used to view a specified test print (printed by a nominated printer), and the observer was asked to rank the amount of leakage present whilst successively illuminated by the three lamp types (from Table 1). The four test conditions performed are itemized in Table 6. Table 6Listing of the four light source ranking experimental conditions. For example, condition “C1” is conducted with test target version Fig. 5(c) printed with the “red” ink of the Canon Printer (ink set 2), viewed through the red lens of glasses 3DG74, and successively illuminated by each of the three lamp types, which equates to a comparison of the “Left Leakage” value. (The meanings of L#, I# and 3DG# are determined from Tables 1–3, respectively). The visual validation test was conducted on the basis of the relative ranking of visual performance because the human visual system is not accurate at determining absolute measurement of brightness (known as “lightness constancy”),39 whereas the human visual system is usually very good at performing relative brightness comparisons. While ranking the glasses, the observers were asked to try to only consider luminance modulation differences between each of the glasses and ignore other optical differences such as overall luminance, relative clarity, and variability of the filter pigments. The marker pen filters usually had a high level of pigment variability. Some of the “cellophane” filters had very poor clarity and softened the image considerably. Luminance modulation of a particular ink swatch is visible as the darkness of the ink swatch relative to the luminance of the unprinted page. 5.Results and Discussion5.1.Light Source Emission SpectraThe spectra of the three sampled light sources are shown in Fig. 4(a). The curves for each display have been scaled such that the maximum of the curve for each lamp is normalized to one. It can be seen that there is a considerable variation between the spectral curves of the different light sources, which is due to each of the lamps having a very different light generation technique. One important aspect to notice in Fig. 4(a) is that the spectrum of the RGB LED lamp (L1) has a low point around 580 nm. This is a good characteristic because the crossover point between the red and the cyan parts of the visual spectrum occurs at around 580 nm. The significance of the correspondence will become more evident later. 5.2.Paper Reflective SpectraThe reflective spectra (independent of source illumination) for two paper stocks are shown in Fig. 4(b). All of the visual testing in this study was performed using a single paper stock (P1: “Fuji Xerox Performer+”). However, a second paper stock (P2: “Double A” 80 gsm A4) was measured and shown here to allow a brief comparison of how the spectra of a different paper stock might vary, but obviously this particular comparison is not exhaustive. One aspect this data does not capture is the presence of fluorescent whitening agents which are sometimes used to “brighten” the look of the paper. These agents work by absorbing UV light and re-emitting blue light to make the paper look less yellow. The current measurement procedure does not capture the presence of fluorescent agents, although the measurement procedure could be modified to allow this effect to be included in the model. 5.3.Ink Set Reflective SpectraThe reflective spectrum (independent of the source illumination and the paper stock) of the “red” and cyan inks for the four printers tested are shown in Fig. 4(c) and 4(d), respectively. One aspect that these graphs reveal is that the spectral performance of the cyan ink of all four printers is particularly poor. Ideally, the cyan ink would attenuate light in the red part of the spectrum ( to 700 nm) and not attenuate light in the blue and green parts of the spectrum ( to 600 nm). It can be seen that although the maximum attenuation (lowest amount of reflection) of the cyan ink is in the red region, the cyan ink also attenuates a substantial amount of light in the blue and green regions. This means that when cyan ink is applied, it not only modulates the red part of the spectrum, but also partly modulates the blue and green parts of the spectrum. The “red” ink has much better spectral shape than the cyan ink, in that it heavily attenuates the blue and green parts of the spectrum, but only lightly attenuates the red part of the spectrum (except for I3, which attenuates about 20% of the red region). The poor spectral quality of the current printing inks is expected to have a large effect on the crosstalk performance of printed anaglyphs and this will be explored further later in the paper using the crosstalk simulation algorithm. 5.4.Glasses Spectral TransmissionThe transmission spectra of the glasses tested in this study are shown in Fig. 4(e) through 4(h). The transmission spectra of the commercial red/blue glasses and hand-made “cellophane” glasses are shown in Fig. 4(e) and 4(f). The transmission spectra of the commercial red/cyan anaglyph glasses and the hand-made “marker-pen” glasses are shown in Fig. 4(g) and 4(h). The poor spectral performance of the “cellophane” glasses are clearly evident in Fig. 4(e) and 4(f). In an ideal pair of anaglyph glasses, the filters would pass the intended color band and block the unwanted color bands, with the blocking of the unwanted channels being the most important. For example, with a red filter, it should pass the red part of the spectrum ( to 700 nm) and block the blue and green parts of the spectrum ( to 570 nm). With most of the “cellophane” glasses, it can be seen that the unwanted color ranges are not well attenuated. Referring to the plots of the red filter of 3DG80 and 3DG81 in Fig. 4(e), it can be seen that these filters do not provide very much attenuation of wavelengths from 400 to 570 nm (the blue and green regions) which will result in significant leakage and therefore high crosstalk. This can be compared with the spectral performance of the red commercial filter 3DG88 in Fig. 4(g), which has very low transmission in the blue-green wavelength range. The marker-pen filters shown in Fig. 4(g) also show a similar insufficient attenuation in the 400 to 570 nm range for the “marker-pen” red filter which will also point to poor crosstalk performance. The crosstalk performance of the glasses will be discussed further from a simulation standpoint below. 5.5.Crosstalk SimulationThe crosstalk simulation program allows a wide range of conditions to be simulated. The results of the crosstalk simulation are illustrated in Fig. 6 across the 288 “display” conditions considered in this project. The simulation program calculates the crosstalk for the left and right eyes separately, and an estimate of the overall crosstalk (calculated as the arithmetic mean of the left and right crosstalk),40 as shown in the figure. The figure allows an inter-condition comparison of the relative performance of the different filters to be easily seen. For example, it can be seen that for the red lens, the simulation predicts that the combination of the RGB LED lamp (L1), the Epson printer (I4) and red lens of glasses 3DG3 provides the lowest crosstalk condition at 11.7% crosstalk. For the cyan lens, the simulation predicts that the combination of the RGB LED lamp (L1), the Canon printer (I2) and the cyan lens of 3DG77 provide the lowest crosstalk condition at 33% crosstalk—which admittedly is a massive amount of crosstalk. More broadly, the simulation also predicts that: the crosstalk in the red lens is generally much lower than crosstalk in the cyan lens; and the RGB LED lamp (L1) generally provides lower crosstalk for both the red and cyan lenses than the other two lamp types (which is probably due to the dark area in the spectral emission of the RGB LED lamp at 580 nm as discussed in Sec. 5.1). Fig. 6Illustration of the results of the printed anaglyph crosstalk simulation for the 12 sets of anaglyph glasses, four printer ink sets and three light sources for (a) red lens, (b) cyan lens, and (c) combined. The symbol key shown in part (b) also applies to parts (a) and (c). 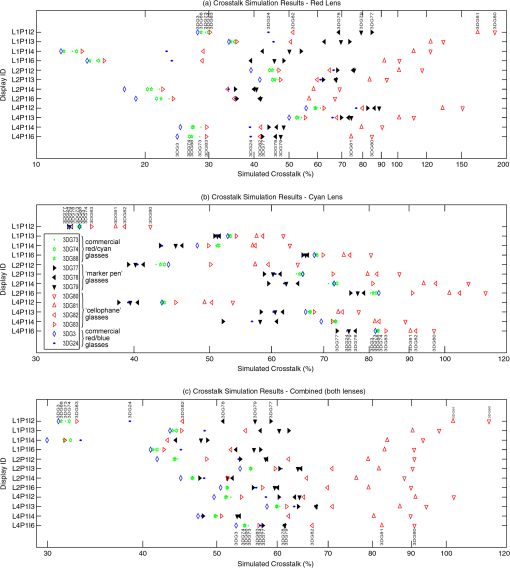 The horizontal axis of both of these plots is shown on a logarithmic scale because it reduces the bunching of the results on the left hand side of the plots, and the human visual response has been described as having a logarithmic-like response to light over a limited range.41,42 With reference to Fig. 6, it can be seen that the rank order of the simulated crosstalk of the tested filters is generally the same from one “display” condition to another. Some cross-overs do occur, and these will be caused by the differences between the shapes of the spectral curves of the different inks and lights and the way these interact with the different shaped spectral curves of the filters. With only a few exceptions, the simulation predicts that the red lens of the commercial anaglyph glasses will offer substantially lower crosstalk than the “hand-made” anaglyph glasses. With the cyan lens, the predicted differences are less clear-cut as they are more closely bunched together, but it can be seen from Fig. 6(b) that the “cellophane” glasses are predicted to mostly have the worst performance. The simulation predicts a good spread in the crosstalk performance of the selection of test filters used in this study—which in turn will aid in the validation of the simulation algorithm. Some of the crosstalk simulation values presented in Fig. 6 are greater than 100% (i.e., the worst performing filters)—this might seem impossible, but this can occur with anaglyph crosstalk with poorly performing filters because the blue and green channels combined (one eye) have a significantly higher luminance than the red channel (the other eye). The simulation also predicts that blue lenses (3DG77, 24, 79, 78, 3) will generally exhibit lower crosstalk than the lenses that have more of a cyan performance (3DG73, 88, 74, 83, 81, 82, 80). This is to be expected because a blue filter blocks more of the green part of the spectrum than a cyan filter does, and hence creates more of a blanking spectral range between the left and right spectral channels. The loss of light from the green part of the spectrum will result in a dimmer image and a loss of color fidelity. It is likely that designers will generally prefer to use cyan lenses due to the brightness and color fidelity problems of blue filters, hence more work is needed to reduce the crosstalk of cyan filters. Figure 6 reveals a further aspect that can affect crosstalk performance: the balancing of the density of the inks. The density of an ink determines how dark the ink appears when it is printed on the page. The density can be controlled either by the concentration of the ink formulation, or the amount of ink which is deposited on the page during the printing process. By way of example, low crosstalk could be achieved in the cyan channel by printing the “red” ink with high density, and using only light density with the cyan ink. However, this will result in high levels of crosstalk in the other eye (in addition to a faint signal image) (due to a relatively darker leakage and a relatively faint signal). This is what could be occurring in the L1P1I2 “display condition” of Fig. 6. The cyan channel exhibits low relative crosstalk compared to the other crosstalk results, however in the red channel it exhibits the opposite with high relative crosstalk compared to the other crosstalk results of the red filters. This leads us to suggest that there may be some benefit in careful balancing of the relative density of the two inks so as to balance the amount of crosstalk in both eyes (while at the same time trying to match the darkness of both channels). We have conducted some work to predict the best density balance to minimize crosstalk, but this work is not ready for publication at this stage. 5.6.Visual Validation ResultsThe visual ranking experiment involved 100 separate crosstalk ranking tasks across five observers, 12 pairs of glasses (two filters in each pair of glasses), four different ink sets, and three different lamp types resulting in 780 separate observations (600 glasses rank observations, 120 ink set rank observations, and 60 lamp rank observations). The results of the visual glasses ranking experiment are illustrated in Fig. 7. The glasses ranking results for each “display” condition (lamp, paper, ink set), observer, and filter color combination are plotted against the corresponding simulated crosstalk ranking for that “display” condition and filter color. A line segment joins the visual ranking with the simulated ranking for each observation. Fig. 7The visual validation test results for the 12 sets of glasses showing observed rank order compared to simulated rank order on the scale of the simulated percentage modulation—per the experimental plan set out in Table 4. Ob1–Ob5 represents the five observers. 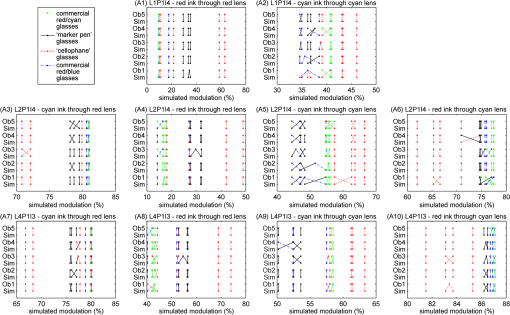 When plotting the ranking results, we had the option of showing the ranking observations with an equal spacing between observations; however, this would give an unrealistic equal visual emphasis on ranking observations regardless of how close or disparate the value is between those particular filters. We therefore decided to plot the results with horizontal axis values which correspond to the simulated percentage modulation values for each pair of glasses. This plotting technique allows us to easily see which conditions the simulation expects to have similar values, and provides more visual emphasis on ranking errors which have greater simulated differences than ranking errors between filters which have small simulated differences. We believe this plotting technique allows a more useful analysis of the data. This same plotting technique was used in one of our previous papers.34 In cases where the observer was unable to distinguish any difference between different filters (i.e., they looked to have the same amount of modulation), observers were allowed to group those glasses together. Glasses that have been grouped together by an observer are plotted with the same horizontal axis value (using the mean of the corresponding simulated crosstalk values). The different groups of anaglyph glasses (commercial red/cyan, commercial red/blue, “marker-pen” and “cellophane”) have been plotted with different colors and line styles, thus allowing the different groups to be easily identified and reveal any trends. Referring to Fig. 7, in cases where the visual ranking agrees with the simulated ranking, the line segments are vertical and do not intersect. In cases where the visual and simulated rankings disagree, there will be a cross-over of the line segments. In general terms the validation results of the glasses ranking experiment, as depicted in Fig. 7, agree very well with the crosstalk simulation ranking results. Across all of the observations, a high proportion (70%) of the observations were ranked in direct agreement with the simulation. It can be seen from the figure that ranking errors (indicated by crossing line-segments) rarely occurred across large simulated modulation value differences. Ranking errors usually only occurred between filters with very similar simulated modulation values. These results are statistically analyzed in the next section. As outlined in Sec. 4.5, two further ranking experiments were conducted—firstly comparing (ranking) the relative performance of the three different lamp types as illustrated in Fig. 8, and secondly comparing (ranking) the relative performance of the four different ink sets as illustrated in Fig. 9. Again it can be seen from these two figures that the validation results of the ink set and lamp ranking experiment agree very well with the crosstalk simulation ranking results. Again a high proportion of the observations were ranked in agreement with the simulation—75% for the ink set ranking and 87% for the lamp ranking. Ranking errors (indicated by crossing line-segments) again only usually occurred between observations with small differences between the simulated modulation values. These results are also statistically analyzed in the next section. Fig. 8The printer ink set ranking results showing observed rank order compared to simulated rank order on the scale of the percentage modulation—per the experimental plan set out in Table 5. These observations were performed using glasses 3DG74. Please note that cyan through red and red through cyan were not tested in this domain in order to reduce the experiment duration per Sec. 4.5. 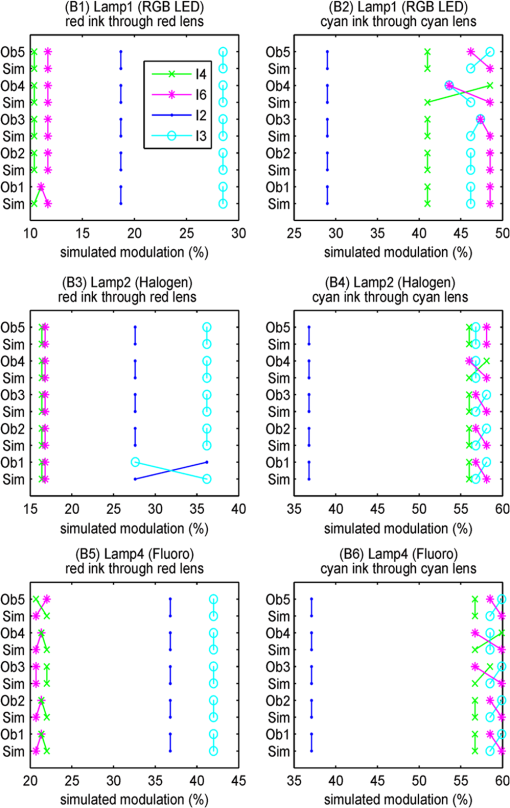 Fig. 9The lamp light source ranking results showing observed rank order compared to simulated rank order on the scale of the percentage modulation—per the experimental plan set out in Table 6. These observations were performed using glasses 3DG74. Please note that cyan through red and red through cyan were not tested in this domain in order to reduce the experiment duration per Sec. 4.5. 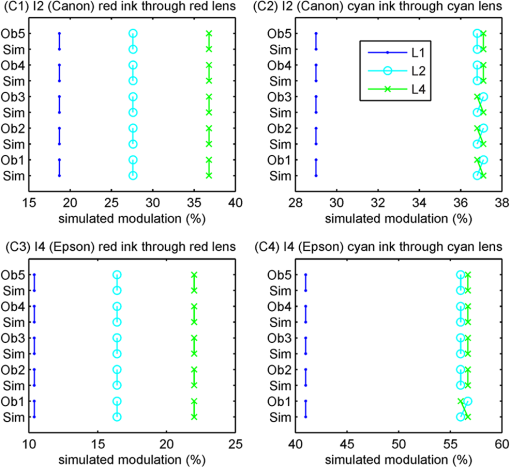 Looking at the plotted results (Figs. 7 to 9), there do not appear to be any consistent ranking reversals in the data across all observers, which would point to an error in the model. There is a consistent number of random rank reversals between observations which have close simulated modulation values, but this would be consistent with an increased difficultly for the observers to do this visual comparison, and not an error with the simulation. 5.7.Statistical AnalysisThe quality of agreement between the visual ranking and the simulated ranking was assessed using two correlation techniques. The first technique, Spearman’s rank correlation,43 is used in biological statistics when one or more of the variables in a dataset consist of only ranks, as is the case with the visual ranking data. The Spearman rank correlation () values were calculated for all of the visual validation observations across the various tested ink, lamp, observer, and filter color combinations and these are presented in Table 7. Table 7Results of the statistical analysis of the glasses visual ranking results. The table shows the correlation data for each “display,” observer and filter color combination, and also the average correlation for each observer using the two correlation techniques. Columns 3-6 show the Spearman’s rank correlation (rs ). Columns 8-11 show the Coefficient of Determination (r2) values calculated using the Pearson product-moment correlation technique as described in the text. Columns 7 and 12 show the average value for each of the observers across all ‘displays’ and filter types using the two techniques. (1 indicates good agreement, 0 indicates poor agreement).
The second analysis technique is based on the Pearson product-moment correlation coefficient44 (also known as the sample correlation coefficient), and its square, the coefficient of determination (). Normally the Pearson technique cannot be applied to ordinal rank order data, however for the purposes of this analysis, the ordinal visual ranks for each condition were transformed into an interval variable by assigning the ranks the values of the percentage modulation from the crosstalk simulation. One advantage of this analysis method is that all ranking errors are considered, but more emphasis is placed on ranking errors between observations with larger simulated crosstalk differences. This second technique is unconventional, however it corresponds well with the plotting technique used in Fig. 7. The Coefficient of Determination () values are presented in columns 8 through 11 of Table 7. The average and value for each of the five observers are shown in columns 7 and 12, respectively of Table 7. The average and values for each observer were calculated as the mean of the 10 correlation results for each observer for each correlation technique. The statistical analysis (Table 7) of the visual ranking results (as plotted in Fig. 7) provides a high level of confidence in the accuracy of the crosstalk simulation algorithm in the glasses domain. It can be seen in Table 7 that 96% of the ranking tests have an value of 0.9 or better, 94% have an value of 0.9 or better, 60% have an value of 0.99 or better, and 20% have an value of 0.99 or better. Another way of analyzing the data is to consider the correlation with the ranking results of each observer to each other in comparison to the correlation of the ranking results of each observer with the simulation. It can be seen in Table 8 that in all but one case, the best correlation for each observer was with the simulation (and not the other observers). This provides further confidence in the glasses dimension of the simulation. Table 8Results of a Pearson cross-correlation between the ranking results of one observer against the other observers and the simulation results for the glasses ranking data illustrated in Fig. 7.
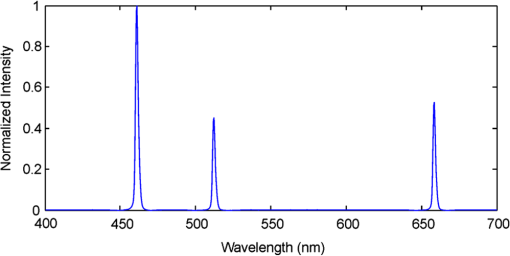
The visual ranking results across the ink set and lamp domains were also statistically analyzed and provide further confidence in the model in these domains. For the ink set domain results (shown in Fig. 8), the mean was 0.805 and mean was 0.963. For the lamp domain results (illustrated in Fig. 9), the mean was 0.900 and the mean was 0.999. It should be noted that there are less observations per domain for the ink (4) and lamp (3) domains compared to the glasses domain, which has 12 options—a factor that may limit the accuracy of the analysis. The statistical analysis of the visual validation experiment has provided a high level of confidence in the accuracy of the printed anaglyph crosstalk simulation model. 6.Simulation of Alternative ScenariosNow that we have established that the printed anaglyph crosstalk simulation model is operating with a high level of accuracy, we can use the model to predict the performance of a number of printed anaglyph crosstalk scenarios we would not otherwise be able to physically replicate easily. Let us consider several such scenarios to further reduce the crosstalk—using the best of the (red/cyan) glasses/ink/lamp combinations revealed in Fig. 6 (i.e., L1P1I2 3DG88) as a starting point. The first scenario is to consider changing the light source used to illuminate the printed anaglyph image. We have already considered the effect of a small selection of light sources on the amount of crosstalk and found that changing from a halogen light source (L2) to an RGB LED light source (L1) resulted in a 13 percentage point drop in crosstalk (from 44% to 31% crosstalk, using ink set I2 and glasses 3DG88). We can also now use the simulation to consider the effect of using a light source which consists of red, green and blue lasers which will have very narrow spectral peaks in the red, green and blue sections of the visual spectrum (we will designate this light source “L5”). The spectrum of such a theoretical light is shown in Fig. 10. It is hoped that the wide spectral bands of no light output would afford a further reduction in crosstalk. Table 9 lists the simulated printed anaglyph crosstalk performance using such a RGB laser light source in comparison to the aforementioned configurations. The simulation predicts that using an RGB laser light source will result in a further drop of crosstalk (now down to 26%) but this is still an unacceptable level of crosstalk—other work suggests that crosstalk levels need to be at least less than 5% for comfortable 3D viewing.7 Further optimization of the actual frequency of the laser spectral peaks may result in a further small improvement, but it is unlikely we will be able to reach an acceptable level of crosstalk by any further changes to the light source alone. Table 9Simulated effect on printed anaglyph crosstalk of changing light sources.
The second scenario considers changing the anaglyph glasses to improve crosstalk. Here we simulate the performance of a pair of anaglyph glasses which have a theoretical “brick-wall” filter performance (i.e., 100% transmission in the pass region and 0% transmission in the blocking region). It would not be possible to physically test “brick-wall” filters in reality because they do not exist, but these simulation results will provide an indication of the absolute limit of lowest crosstalk performance achievable by optimization of the glasses alone. The pass-bands of the “brick-wall” filters were 620 to 700 nm for the red filter and 400 to 560 nm for the cyan filter with other wavelengths blocked. Table 10 lists the simulated anaglyph crosstalk performance of the four test conditions–two with glasses 3DG88 and two with the glasses changed to the “brick-wall” filters. The simulation results indicate that even with a perfect pair of anaglyph glasses, none of the anaglyph prints were able to exhibit zero crosstalk; this is because the inks we tested have significant attenuation in out-of-band wavelengths. For the better of the two conditions (L1P1I2), the use of “brick-wall” glasses only resulted in a 10% improvement of combined crosstalk (both eyes) but this improvement is only achievable in theory, which indicates that there is limited scope for the further reduction in crosstalk by any further changes to the anaglyph glasses alone. Table 10Simulated effect on printed anaglyph crosstalk of using theoretical “brick-wall” filter anaglyph glasses.
The third scenario considers the effect of changing the spectral response of the printer inks. As can be seen in Fig. 2, the spectral response of a typical yellow ink has a good spectral characteristic for anaglyph purposes—it has low attenuation in the out-of-band range ( to 700 nm), it has high attenuation in the in-band range ( to 480 nm), and a reasonably fast change from high attenuation to low attenuation (in the region 480 to 520 nm). Unfortunately the cyan and magenta inks typically do not show such a good spectral performance, particularly the cyan. For the purposes of this scenario, hypothetical red and cyan ink spectra were constructed based on the spectrum of an example yellow ink, such that the new hypothetical red and cyan inks have low attenuation in the out-of-band regions, high attenuation in the in-band regions, and a fast change from high-attenuation to low-attenuation, like that of the example yellow ink. The spectra of the proposed hypothetical red/cyan inks are shown in Fig. 11. Fig. 11The reflectance spectra of the hypothetical red/cyan ink set compared to the “red” and cyan inks of I2. 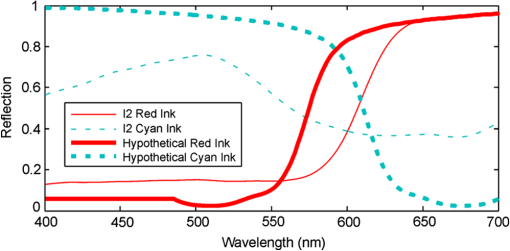 The simulation results of using the hypothetical inks are shown in Table 11. It can be seen that the hypothetical inks provide a substantial improvement in crosstalk performance—as much as an 84% reduction. The predicted overall crosstalk of the L2P1 3DG88 condition of only 8.6% is very encouraging and is approaching an acceptable level of crosstalk which other work suggests needs to be much less than 5%.7 It is probable that further optimization of the spectra of the red/cyan ink set can lead to further reductions in printed anaglyph crosstalk. Table 11Simulated effect on printed anaglyph crosstalk of using improved red/cyan inks.
An illustration of how changes to the three domains of printed anaglyph 3D images have on the amount of crosstalk is provided in Fig. 12. It can be seen that the domain which has the biggest effect on reducing the amount of crosstalk is the ink set domain. It can also be seen that the RGB LED lighting and 3DG88 anaglyph glasses (middle circle of Fig. 12) seems to achieve near the maximum gain achievable by changes in the lighting and glasses domains, whereas we believe there remains considerable scope for improvement in the ink set domain. Fig. 12An illustration of the effect of making changes in the various domains of printed anaglyph images (glasses domain, ink set domain, and illumination domain) has on the amount of crosstalk. The circle sizes (area) are proportional to the simulated amount of crosstalk for each condition. The simulation only conditions are shown as dotted circles. 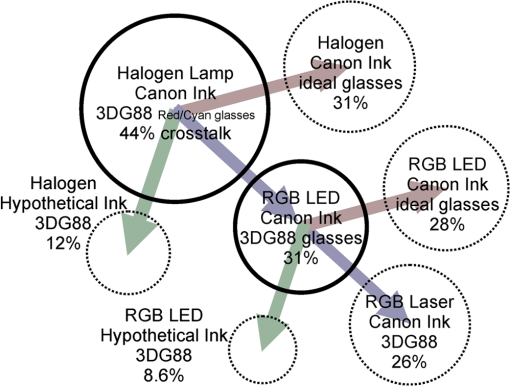 The results of these three simulation scenarios illustrate the advantages that crosstalk simulation can provide in predicting the crosstalk performance of printed anaglyph images. In this case, the simulations indicate that there is significantly more scope for reduction in anaglyph crosstalk by the use of more spectrally pure inks than might be gained from further improvements to the spectral performance of anaglyph glasses. The simulation and the visual validation experiment have also confirmed that there is some scope for improving crosstalk performance by using different light sources, however the simulation indicates that we are probably close to the maximum advantage obtainable with the tested RGB LED light source (in the case of red/cyan anaglyphs). As mentioned in Sec. 3, the equations developed for calculating crosstalk in printed anaglyphs Eqs. (1) through (13) are similar but notably different to the crosstalk equations for emissive displays.7 This difference also extends to the equations used to calculate crosstalk from light measurement device readings off an anaglyph print. Crosstalk Eqs. (11) and (12) can therefore be expressed as where and are the crosstalk at each eye—often expressed as a percentage; and , , , , , and are the luminance as measured behind the glasses at the left or right eye position (first subscript), with the desired eye channel ink applied (—black) or the desired eye channel ink not applied (–white) (second subscript), and with the undesired eye channel ink applied (–black) or the undesired eye channel ink not applied (–white) (third subscript). For example, in the case of a red-left/cyan-right anaglyph print, is the luminance measured from the left eye position behind the red lens when there is no ink applied to the white page, is the luminance measured from the left eye position behind the red lens when only cyan ink (the desired ink for this eye channel) is applied to the page, and is the luminance measured from the right eye position behind the cyan lens when only cyan ink (the undesired ink for this eye channel) is applied to the page. This particular luminance variable expression can appear confusing; however it is expressed this way in order to correspond with the variable definitions used to express the measurement of crosstalk in emissive displays.77.ConclusionThis paper has presented the development and validation of a crosstalk simulation model for printed anaglyph images. The model is significant in that it allows for the first time a detailed analysis of the process of crosstalk in printed anaglyph 3D images. Printed anaglyph 3D images can often exhibit a lot of crosstalk so it is very useful to have a tool that allows the exploration of techniques to reduce crosstalk in such images. The model has already allowed us to propose a solution that may reduce crosstalk to as low as 8.6%. The model can very quickly simulate the crosstalk performance of a huge number of input combinations (glasses, inks, papers, and lights) to determine optimum combinations—a process that would be impossible to conduct physically. The model can be used to intelligently guide research effort before time and money is expended on physical testing. In summary, this paper has identified seven ways of reducing crosstalk with printed anaglyph 3D images:
Many of these items cannot be achieved with current ink-jet and color laser printers, but can with offset printing. The information presented in this paper should facilitate a significant improvement in the 3D image quality of this very widely used 3D presentation technique. AcknowledgmentsThe authors wish to acknowledge the support of Alec Duncan for his assistance with the manuscript; Dan Marrable, Ming Lim, and Glen Lawson for their assistance with the optical test equipment; and Angela Recalde, Matthew Koessler, Michael Biddle, and Ming Lim for their assistance with the visual validation tests. ReferencesR. LabbeD. E. Klutho,
“Publishing stereoscopic images,”
Proc. SPIE, 7237 72370J
(2009). http://dx.doi.org/10.1117/12.811942 PSISDG 0277-786X Google Scholar
V. K. Walworth,
“Light polarization in support of stereoscopic display,”
Opt. Eng., 51
(2), 021104
(2012). http://dx.doi.org/10.1117/1.OE.51.2.021104 OPEGAR 0091-3286 Google Scholar
V. C. BarberD. A. Brett,
“Colour bombardment—a human visual problem that interferes with the viewing of anaglyph stereo material,”
Scan. Electron Microsc., 2
(Pt. 2), 495
–498
(1982). SEMYBL 0586-5581 Google Scholar
A. J. WoodsK. L. YuenK. S. Karvinen,
“Characterizing crosstalk in anaglyphic stereoscopic images on LCD monitors and plasma displays,”
J. Soc. Inform. Disp., 15
(11), 889
–898
(2007). http://dx.doi.org/10.1889/1.2812989 JSIDE8 0734-1768 Google Scholar
L. Lipton,
“Glossary,”
(2010) http://lennylipton.wordpress.com/2009/03/16/glossary/ March ). 2010). Google Scholar
A. J. Woods,
“How are crosstalk and ghosting defined in the stereoscopic literature?,”
Proc. SPIE, 7863 78630Z
(2011). http://dx.doi.org/10.1117/12.877045 PSISDG 0277-786X Google Scholar
A. J. Woods,
“Crosstalk in stereoscopic displays: a review,”
J. Electron. Imag., 21
(4), 040902
(2012). http://dx.doi.org/10.1117/1.JEI.21.4.040902 JEIME5 1017-9909 Google Scholar
F. L. KooiA. Toet,
“Visual comfort of binocular and 3D displays,”
Displays, 25
(2–3), 99
–108
(2004). http://dx.doi.org/10.1016/j.displa.2004.07.004 DISPDP 0141-9382 Google Scholar
Y.-Y. YehL. D. Silverstein,
“Limits of fusion and depth judgement in stereoscopic color displays,”
Hum. Factors, 32
(1), 45
–60
(1990). http://dx.doi.org/10.1177/001872089003200104 HUFAA6 0018-7208 Google Scholar
I. TsirlinL. M. WilcoxR. S. Allison,
“The effect of crosstalk on the perceived depth from disparity and monocular occlusions,”
IEEE Trans. Broadcast., 57
(2), 445
–453
(2011). http://dx.doi.org/10.1109/TBC.2011.2105630 IETBAC 0018-9316 Google Scholar
H. SanftmannD. Weiskopf,
“Anaglyph stereo without ghosting,”
Comput. Graph. Forum, 30
(4), 1251
–1259
(2011). http://dx.doi.org/10.1111/j.1467-8659.2011.01984.x CGFODY 0167-7055 Google Scholar
I. IdesesL. Yaroslavsky,
“Three methods that improve the visual quality of colour anaglyphs,”
J. Opt. A Pure Appl. Opt., 7
(12), 755
–762
(2005). http://dx.doi.org/10.1088/1464-4258/7/12/008 JOAOF8 1464-4258 Google Scholar
A. J. WoodsC. R. Harris,
“Comparing levels of crosstalk with red/cyan, blue/yellow, and green/magenta anaglyph 3D glasses,”
Proc. SPIE, 7524 75240Q
(2010). http://dx.doi.org/10.1117/12.840835 PSISDG 0277-786X Google Scholar
M. A. Purnell,
“Casting, replication, and anaglyph stereo imaging of microscopic detail in fossils, with examples from conodonts and other jawless vertebrates,”
Palaeont. Electron., 6
(2), 1
–11
(2003). Google Scholar
E. Dubois,
“A projection method to generate anaglyph stereo images,”
in Proc. IEEE Int. Conf. on Acoustics, Speech, and Signal Process.,
1661
–1664
(2001). Google Scholar
W. R. SandersD. F. McAllister,
“Producing anaglyphs from synthetic images,”
Proc. SPIE, 5006 348
–358
(2003). http://dx.doi.org/10.1117/12.474130 PSISDG 0277-786X Google Scholar
D. F. McAllisterY. ZhouS. Sullivan,
“Methods for computing color anaglyphs,”
Proc. SPIE, 7524 75240S
(2010). http://dx.doi.org/10.1117/12.837163 PSISDG 0277-786X Google Scholar
V. M. Tran,
“New methods of rendering anaglyph stereoscopic images on CRT displays and photo-quality ink-jet printers,”
University of Ottawa,
(2005). Google Scholar
R. Z. ZengH. Z. Zeng,
“Printing anaglyph maps optimized for display,”
Proc. SPIE, 7866 78661S
(2011). http://dx.doi.org/10.1117/12.872644 PSISDG 0277-786X Google Scholar
P. Wimmer,
“Anaglyph methods comparison,”
(2013) http://www.3dtv.at/knowhow/anaglyphcomparison_en.aspx March ). 2013). Google Scholar
A. J. WoodsT. Rourke,
“Ghosting in anaglyphic stereoscopic images,”
Proc. SPIE, 5291 354
–365
(2004). http://dx.doi.org/10.1117/12.537424 PSISDG 0277-786X Google Scholar
R. Zone,
“Good old fashion anaglyph: high tech tools revive a classic format in Spy Kids 3-D,”
Stereo World, 29
(5), 11
–13
(2002). Google Scholar
“Louis Ducos du Hauron,”
Encyclopædia Britannica,
(2012) http://www.britannica.com/EBchecked/topic/172961/Louis-Ducos-du-Hauron July 2012). Google Scholar
A. F. Watch,
“The anaglyph: a new method of producing the stereoscopic effect,”
J. Franklin Inst., 140
(6), 401
–405
(1895). http://dx.doi.org/10.1016/0016-0032(95)90278-3 JFINAB 0016-0032 Google Scholar
G. Sharmaet al.,
“Illuminant multiplexed imaging: special effects using GCR,”
in Proc. 11th Color Imaging Conference: Color Science and Engineering Systems, Technologies, and Applications,
266
–271
(2003). Google Scholar
A. J. WoodsC. R. Harris,
“Using cross-talk simulation to predict the performance of anaglyph 3-D glasses,”
J. Soc. Inform. Disp., 20
(6), 304
–315
(2012). http://dx.doi.org/10.1889/JSID20.6.304 JSIDE8 0734-1768 Google Scholar
B. FraserC. MurphyF. Bunting, Real World Color Management, Peachpit Press, San Francisco, California
(2004). Google Scholar
L. A. Taplin,
“Spectral modeling of a six-color inkjet printer,”
Rochester Institute of Technology,
(2001). Google Scholar
A. StockmanL. T. Sharpe,
“Luminous energy function (2 degree, linear energy),”
(2007) http://www.cvrl.org/cvrlfunctions.htm July 2011). Google Scholar
A. Stockmanet al.,
“The dependence of luminous efficiency on chromatic adaptation,”
J. Vision, 8
(16), 1
–26
(2008). http://dx.doi.org/10.1167/8.16.1 1534-7362 Google Scholar
R. BlakeR. Sekuler, Perception, 5th ed.McGraw Hill, Boston, Massachusetts
(2006). Google Scholar
, “Information display measurements standard (version 1.03),”
(2012) http://icdm-sid.org/ Google Scholar
S. S. Stevens,
“On the psychophysical law,”
Psychol. Rev., 64
(3), 153
–181
(1957). http://dx.doi.org/10.1037/h0046162 PSRVAX 0033-295X Google Scholar
Z. XieT. G. Stockham Jr.,
“Toward the unification of three visual laws and two visual models in brightness perception,”
IEEE Trans. Syst. Man Cybern., 19
(2), 379
–387
(1989). http://dx.doi.org/10.1109/21.31040 ITSHFX 1083-4427 Google Scholar
J. H. McDonald, Handbook of Biological Statistics, 221
–223 2nd ed.Sparky House Publishing, Baltimore, Maryland
(2009). http://udel.edu/~mcdonald/statspearman.html Google Scholar
R. E. WalpoleR. H. Myers, Probability and Statistics for Engineers and Scientists, 347 Collier Macmillan, New York
(1985). Google Scholar
Biography Andrew J. Woods is a research engineer at Curtin University’s Centre for Marine Science & Technology in Perth, Australia. He has MEng and BEng (Hons1) degrees in electronic engineering. He has expertise in the design, application, and evaluation of stereoscopic imaging systems for industrial and entertainment applications. He has served as co-chair of the Stereoscopic Displays and Applications conference since 2000.  Chris R. Harris is a graduate of Curtin University with a bachelor’s degree in applied physics and has interests in electronics and information technology. He is currently employed by Murdoch University. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||