|
|
1.IntroductionCataract is one of the major causes of vision loss in the aging population. The common treatment for cataract is the replacement of the natural lens by an intraocular lens (IOL). IOLs are implanted in the capsular bag, following phacoemulsification and aspiration of the crystalline lens material. In an intracapsular procedure, the IOL is inserted in the capsular bag through a circular window in the anterior capsule (capsulorhexis), with the lens haptics pressing against the equatorial region of the capsular bag. The stability of the IOL in the capsular bag depends on the material and design of the haptics. With state-of-the art monofocal IOLs, IOL tilt and decentration are generally of similar amounts of those of the natural crystalline lens.1 Although originally the main goal of a cataract treatment was to eliminate scattering, IOLs have evolved enormously, first to additionally correct for refractive errors, but more recently, to compensate for high order aberrations (HOA), particularly spherical aberration. Also, new IOL designs aim at correcting presbyopia, either by expanding the depth-of-focus of the eye (multifocal IOLs—M-IOLs) or by dynamic changes of refractive power (accommodating IOLs—A-IOLs). With the increased sophistication of IOL designs, the impact of the IOL position becomes more critical. The aimed correction of corneal HOA by aspheric IOLs may be compromised by the induction of other HOA by a tilted/decentered lens.2 The performance of refractive M-IOLs (generally with concentric or segmented near/far regions) is critically affected by potential misalignments of the IOL.3 Finally, tilts and decentrations occurring with the only U.S. Food and Drug Administration (FDA)-approved A-IOL may also play a role in its function.4 Measurement of tilt and decentration of IOLs in pseudophakic eyes is therefore important as an endpoint for treatment, particularly with premium IOLs. On the other hand, in combination with biometrical and anatomical ocular data, knowledge of IOL and eye alignment is important in the development of customized computer eye models, which give insights into the relative contribution of different factors to optical performance with IOLs (Refs. 5 and 6). Several methods have been presented to measure IOL tilt and decentration. Purkinje imaging relies on the acquisition of pupillary images containing the image formed by the reflexes of the anterior cornea and anterior and posterior lens (Purkinje images I, III, and IV). The relative positions of PI, PIII, and PIV with respect to the pupil center are proportional to the eye rotation, IOL tilt, and IOL decentration.7,8 Purkinje imaging has been used successfully for lens phakometry,6,9–11 and for measurements of tilt and decentration of the natural lens,12,13 and IOLs (Refs. 1 and 14–15.16). The device is simple and the measurement typically robust, although it may be subject to some limitations: difficulties in the association of the images to the corresponding reflecting surfaces [some authors have solved this by projecting a semicircular ring of light-emitting diodes (LEDs) yielding relative inverted images for PI and PIV (Ref. 17)]; overlapping of the different Purkinje images (usually overcome by eccentric illumination and image acquisitions at different eccentric fixations);9 and requirement of ocular geometrical and biometrical information (normally obtained from the other instruments). Scheimpflug imaging has also been used to estimate tilt and decentration of IOLs, by the analysis of the orientation and shift of the lens in cross-sectional images of anterior segment of the eye.1,18 The three-dimensional (3-D) tilt and decentration can be obtained from sinusoidal fitting of the two-dimensional (2-D) coordinates. Although the method is direct (i.e., relies on the direct viewing of the lens), it is subject to several limitations: refraction distortion of the lens images and relatively sparse meridional sampling. IOL tilt and (to a lesser extent) decentration from this technique were in good agreement with Purkinje-based measurements.1 The accuracy and precision of the Scheimpflug data were tested in measurements in an artificial eye, with a discrepancy from nominal values of 0.24 deg, on average, for tilt (0.28 deg for Purkinje-based tilt), and 0.23 mm, on average, for decentration (0.01 mm for Purkinje-based decentration). Spectral OCT (sOCT) has been recently demonstrated as a quantitative 3-D full anterior segment biometer.19 After quantitative image analysis (including fan and optical distortion corrections), OCT provides accurate anterior and posterior corneal topography and pachymetry,20,21 anterior and posterior lens topography,22 pupilometry, and anterior chamber depth.19 In addition, the direct view of the lens also allowed estimates of tilt and decentration.4,19,23,24 In this study, we developed Purkinje-based methodology from the anterior segment en face OCT images. The technology resembles the Purkinje method, since three spots are observed in the en face OCT images. These spots are originated from the reflections of light in the anterior surface of the cornea and anterior and posterior surfaces of the lens, although, in contrast to the standard Purkinje method, the spots are not formed by the entire area of the ocular surfaces. Instead, the OCT system collects the scattered light reflected back from the tissue, and when the reflected ray direction coincides with the OCT axis, a strong specular reflection is captured in the test arm of the OCT, producing a bright spot in the en face OCT images. Unlike in the standard Purkinje method, which relies on the images in a single plane of focus, the tomographic information of the OCT images allows one to relate each reflection with the corresponding surface, as well as to avoid image overlapping. The Purkinje image analysis (estimation of coefficients in a set of linear equations) requires assumption of an eye model. The assumption of a general computer eye model results in a decrease in the accuracy of the tilt and decentration estimates in Ref. 9. Instead, individual anatomical and biometrical parameters are used, generally obtained from corneal topography or keratometry, optical biometry, and Purkinje phakometry. These parameters can be retrieved from the same OCT dataset.19,25 In this study, we demonstrate the measurement of IOL tilt and decentration from OCT images, which used a Purkinje-based analysis. The method was validated on an artificial model eye (with set values of lens tilt and decentration) and tested in five pseudophakic eyes with implanted A-IOLs (where the en face OCT Purkinje-based estimates of IOL tilt and decentration were compared to direct estimates from distortion-corrected 3-D OCT images). 2.Materials and Methods2.1.Laboratory-Based Spectral Optical Coherence Tomography (sOCT) SystemThe sOCT system is based on a fiber-optics Michelson interferometer configuration with a superluminescent diode SLD (, ; Superlum, Ireland) as a light source and a spectrometer consisting of a volume diffraction grating and a 12-bit line-scan CMOS camera with 4096 pixels (Basler sprint spL4096-140k; Basler AG, Germany) as a detector. The sOCT system used in the measurements has been described in detail in previous publications.26 The acquisition rate was set to , resulting in a typical 3-D dataset acquisition time of 0.72 s. The horizontal and vertical scanning is produced by galvanometer optical scanners (Cambridge Technology Inc., Bedford, Massachusetts), driven by an analog input/output card (National Instruments, Austin, Texas). The axial range of the instrument is 7 mm in depth, resulting in a theoretical pixel resolution of 3.4 μm. The axial resolution predicted by the coherence length of the superluminescent diode laser source is 6.4 μm. The lateral sampling resolution ranged between 0.04 and 0.2 mm. Custom-algorithms correct the OCT data from fan distortion (arising from the scanning architecture) and optical distortion (due to the refraction in the optical surfaces).20 Dedicated image processing routines allow the segmentation of the optical surfaces and quantification of their geometry.20–22,25 2.2.Artificial EyeA water-cell model with a PMMA contact lens simulating a spherical cornea (7.80 mm and 6.48 mm anterior and posterior radii of curvature, respectively, and 0.5 mm central thickness) and an IOL (aspheric biconvex IOL) mounted on a micrometer stage and rotational stage was used for testing. The water-cell eye model is similar to that reported in previous work,1,19 except for the IOL. In this work, we used in the artificial eye the same A-IOL type (Crystalens AO 23.5 D) that was implanted in the patients under test. The geometry of the A-IOL was characterized using a microscopy-based noncontact optical profilometry (Sensofar, PLu2300, Barcelona, Spain) with 0.1-μm nominal precision in vertical measurements.27 Both anterior and posterior surface topographies of the lens were measured in a range ( points equispaced by 0.11 mm). The profiles were fitted with conics using custom routines written in MATLAB (Mathworks, USA). Potential tilts of the mounted IOL in the profilometric measurements were considered and removed.27 The measurements were repeated five times and the mean values are shown in Table 1. Table 1Radii of curvature, axial biometry, and refractive indices, in the physical model eye, and the five patient eyes.
The refractive index of the cornea at the OCT wavelength was calculated by dividing the central optical path length obtained from the OCT images by the nominal geometrical central thickness (, group refractive index at 840 nm). The thickness of the IOL (Crystalens AO 23.5 D) was measured using the profilometry system, and its refractive index was also calculated from the OCT images (, group refractive index at 840 nm). Measurements were obtained for the artificial eye with the lens in air (i.e., cell not filled in with water) and in water. The IOL was tilted inside the water-cell eye from to 5 deg in 1-deg steps and decentered from to 1.9 mm in 0.6-mm steps. 2.3.PatientsImages were collected in five eyes of four patients ( years old) 90 days after the IOL implantation (Crystalens A-IOL, Bausch and Lomb, Rochester, New York). Biometrical data on these patients have been previously reported as part of a larger study aiming at characterizing the performance of these IOLs (Ref. 4). Onlypatients implanted with 23.5-D power IOLs were selected (as this IOL was available for in vitro measurements). This study was approved by the Institutional Review Boards and followed the tenets of the Declaration of Helsinki. Clinical ophthalmological examination and surgery were performed at the Fundación Jiménez-Díaz Hospital (Madrid, Spain). Measurements in postoperative patients were performed under mydriasis (phenylephrine 10%). The subjects were stabilized using a bite bar and aligned with the OCT axis centered at the specular corneal reflection while the patient fixated on a reference E-letter target projected on a minidisplay at optical infinity. A total of six sets of postoperative (three repeated images for the cornea and IOL, respectively) measurements were obtained. All 3-D sets of data contained the iris volume, which was used as the reference for merging the images. In order to minimize the impact of motion artifacts, the image acquisition time to complete the whole measurement was set to 0.72 s. The SLD power exposure was fixed at 800 μW and focus was changed by an automatic displacement system to achieve optimal imaging of the different anterior segment structures (cornea and IOL). Measurements were collected on a zone, using 50 B-Scans composed of a collection of 360 A-Scans, providing a sampling resolution of 0.04 mm for horizontal and 0.2 mm for vertical meridians. 2.4.OCT Image ProcessingThe image processing algorithm for geometrical characterization of the OCT images, described in detail in the previous studies19–22,25,28,29 comprises: image denoising; statistical thresholding; volume clustering; multilayer automatic segmentation; pupil center registration; 3-D volume merging of the cornea and IOL images, obtained in two different acquisitions; geometrical distances calculation; fan distortion correction; optical distortion correction; and surface fitting to spherical surfaces in a 3-mm diameter optical zone with respect to the corresponding surface apex. Anterior segment biometry, including central corneal thickness (CCT), anterior chamber depth (ACD), intraocular lens thickness (ILT), intraocular lens position (ILP), and lens IOL tilt (IT), were computed from the corrected 3-D OCT images. The refractive indices used in the calculations are reported in Table 1. 2.5.Purkinje-Like OCT MethodFigure 1(a) shows 3-D OCT anterior segment images, with the Purkinje-like reflex positions identified. The Purkinje-like analysis can be summarized in five steps: (1) collection of a volumetric dataset, (2) generation of image intensity values in the axial direction, (3) pupil segmentation and identification of the positions of the specular reflexes in the different surfaces (Purkinje-like images positions, PI, PIII, and PIV) [Fig. 1(b)]. The reflexes PI, PIII, and PIV are easily identified by checking the corresponding OCT B-Scan image [Fig. 1(c)]. The position of the reflexes is referred to the center of the pupil. Fig. 1(a) Three-dimensional (3-D) optical coherence tomography (OCT) image (example is for S#3, OD); (b) en face OCT image showing the pupil merging, the locations of PI, PIII, and PIV in red and pupil center in yellow; (c) PI (left), PIII (center), and PIV (right) in OCT B-Scan images. 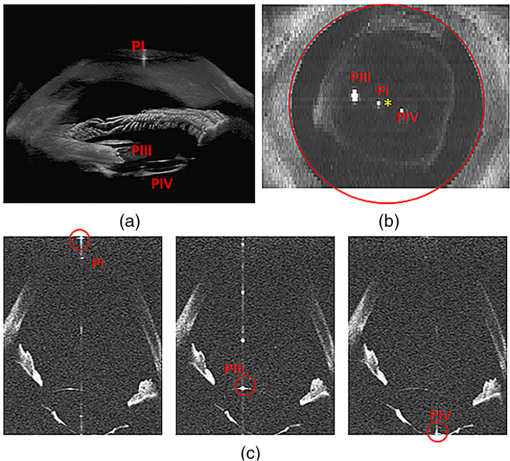 The method for estimating IOL alignment is based on that described in the previous works.7–9 This method assumes a linear relationship between Purkinje-like image positions (PI, PIII, PIV) and rotation of the eye (), tilt (), and decentration (): A computer eye model was set in ZEMAX using biometrical information of anterior and posterior surfaces of the cornea obtained from OCT measurements19 and the IOL geometry obtained from noncontact profilometry, as described in Sec. 2.2. To calculate the position of the reflex on the different surfaces, routines were written in ZEMAX to search the rays that, following reflection from a surface, exit the eye parallel to the optical axis. Although the standard Purkinje method studies the image created by all the rays passing through the pupil, the spots visible in en face OCT images are created by a few rays only. Although different, the standard Purkinje images and the Purkinje-like reflections in OCT en face images are very close. We calculated in a standard computer eye model that the difference in position of the images between the two methods (for PI, PIII, and PIV) was always below 20 μm. To obtain coefficients , , and , in Eq. (1), and (no tilt and no decentration) were set in the computer eye model, and the Purkinje-like reflex positions were estimated for different rotation angles. A linear fit of the displacement of the reflex provided the value of the coefficients , , and . The same procedure was repeated for and (setting and ) and and (with and ).8 Eye rotation () and lens tilt and decentration ( and ) were obtained from the inversion in Eq. (2), using the positions of the experimental reflexes (P1, P3, and P4). 3.Results3.1.Validation on a Water-Cell Physical Model EyeThe developed methodology was tested on the physical model eye described before. The corresponding coefficients of Eq. (1) were computed for the artificial eye (see Table 2 for both the model eye in air and filled in with water). Table 2A–G coefficients in Eq. (1) for the physical model eye in air and water and the five eyes of the study.
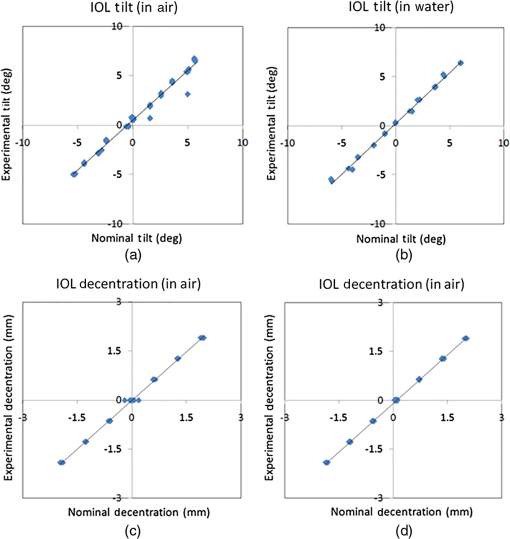
Figure 2 shows the experimental tilt and decentration measured in the physical model eye, against the nominal set values of tilt and decentration, for the IOL in air (a, c) and water (b, d). There is a high correspondence between the experimental and nominal values: , , for IOL tilt in air; , , for IOL tilt in water; , , for IOL decentration in air; , , for IOL decentration in water. The average difference between nominal and experimental values was for tilt and for decentration. 3.2.IOL Tilt and Decentration in PatientsMeasurements were performed on five eyes of four patients, all implanted with a 23.5 D Crystalens AIOL. The biometrical parameters necessary to build the computer eye model were obtained from OCT (anterior and posterior corneal radius, corneal thickness, ACD)4 and from noncontact profilometry (anterior and posterior IOL radii of curvature and thickness). Table 1 shows the corresponding parameters for all five eyes. The two sets of coefficients for tilt and decentration correspond to two different realizations of the artificial eye model. (The anterior chamber depth was enlarged for IOL tilt measurements to allow proper positioning of the platform holding inside the chamber). IOL tilt is defined as the angle between the IOL axis and the pupillary axis, where the IOL axis is the line joining the centers of curvature of the IOL and the pupillary axis joining the center of curvature of the cornea and the pupil center. IOL decentration is defined as the distance between the IOL center and the pupil center. According to the existing conventions,6 positive horizontal decentration stands for nasal decentration (in right eyes) and temporal decentration (in left eyes), and vice versa for negative; and positive vertical decentration for superior, and negative for inferior. Positive tilt around the horizontal axis (tilt ) indicates that the superior edge of the lens is moved forward. Negative tilt around the vertical axis (tilt ), in right eyes, indicates that the temporal edge of the lens is moved forward, and, in left eyes, indicates that the nasal edge of the lens is moved forward. We did not find consistent mirror symmetry in the orientation of tilt or decentration in these eyes (Fig. 3). The average tilt around -axis was in right eyes and in left eyes (Purkinje-like), and in right eyes and in left eyes (OCT). Average tilt around the -axis was 2.15 deg in right eyes and 1.65 deg in left eyes (Purkinje-like) and 2.93 deg in right eye and 2.14 deg in left eyes (OCT). Average decentration in the horizontal axis was in right eyes and 0.00 mm in left eyes (Purkinje-like), and in right eyes and 0.11 mm in left eyes (OCT). Average decentration in the vertical axis was . The average standard deviations for repeated measurements of tilt were 0.47 deg (Purkinje-like) and 0.58 deg (OCT). The standard deviation for repeated measurements of decentration was 0.04 mm (Purkinje-like) and 0.06 mm (OCT). Fig. 3Coordinates of IOL tilt (a) and (b) decentration (b) in right and left eyes, in all five eyes of the study. Solid symbols represent data obtained using the Purkinje-like OCT-based method. Open symbols represent data obtained directly from distortion-corrected 3-D OCT images (Ref. 19). Square, rhombus, and round represent right eyes (OD) while triangle and rectangle represent left eyes (OS). Each color (color online only) represents a different eye. Error bars stand for standard deviations of repeated measurements. 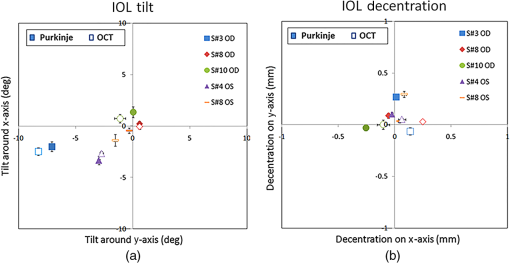 Figure 4 compares the coordinates of tilt (a, b) and decentration (c, d) measured with both techniques. There was a high correlation between both estimates particularly for tilt (slope: 1.18, , , for tilt around -axis; slope: 0.92, , for tilt around -axis), and slightly lower, not reaching statistical significance, for decentration (slope: 0.62, , , for decentration on -axis; slope: , , for decentration on -axis). Figure 5 shows a Bland–Altman plot for tilt measurements (a) and for decentration measurements (b), i.e., average of tilt/decentration coordinates from Purkinje and OCT versus difference of tilt/decentration coordinates from both methods. The average difference in tilt from both methods was , with the 95% limits of agreement to 0.416 deg. All tilt coordinates from either method were within the confidence interval and 40% differed by . The average difference in decentration from both methods was , with the 95% limits of agreement to 0.033 mm. All decentration coordinates from either method were within the confidence interval and 50% differed by . Fig. 4Correlation between data obtained from Purkinje-like and OCT methods for IOL tilt (a, b) and decentration (c, d) in all five eyes of the study. 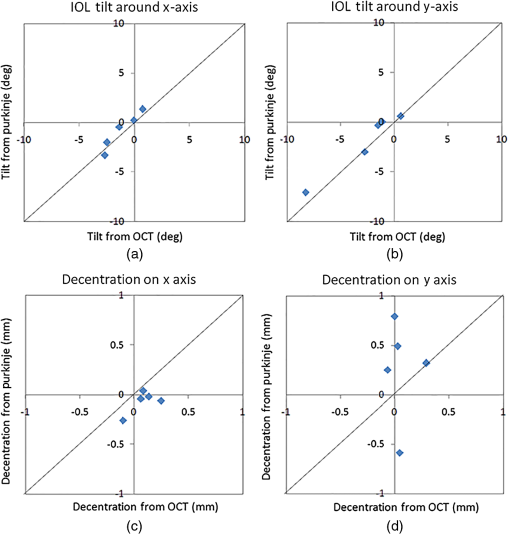 Fig. 5Bland–Altman plot-differences between Purkinje-like and OCT estimates of tilt (a) and decentration (b). Horizontal lines represent the mean difference ( and , respectively) and 95% limits of agreement. 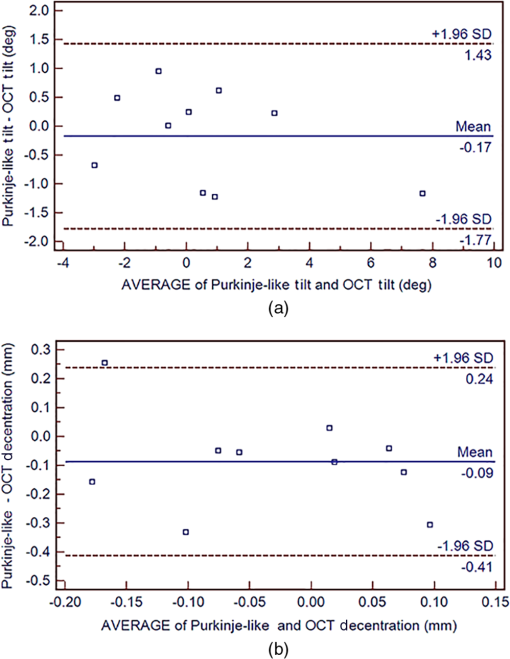 Although all the estimates are obtained from the same image dataset, the causes for the slight discrepancies may arise from the 3-D nature of the reference axes in OCT and the 2-D nature in Purkinje. The center of the pupil in the OCT images is given by lateral and axial coordinates, which may result in a slightly different pupillary axis. Besides, the pupil plane itself may show some tilt, while the pupil edges in the Purkinje-like method are obtained from the frontal projection (2-D coordinates) in the en face OCT images. We simulated the Purkinje images of a computer 3-D model eye built using the estimates for tilt, decentration, and eye rotation obtained from the Purkinje-like method, using ZEMAX and found that the positions of the simulated PI, PIII, and PIV were within 0.004 mm, 0.011 mm, and 0.004 mm, respectively, from the experimental Purkinje images (see Fig. 6, showing an example from eye S# 8 OS). 4.DiscussionWe have developed and validated a new method of measurement of IOL tilt and IOL decentration from the en face OCT anterior segment images showing Purkinje-like reflections from the anterior cornea and anterior and posterior lens. The images are similar to those obtained by the standard Purkinje method images, which are specular reflections formed at the ocular surfaces and matched in position. The Purkinje-like reflex locations are assumed to be linear combinations of eye rotation, lens tilt and decentration, with the weighting coefficients dependent on the eye’s biometry (and easily derived by computations on computer eye models), lens tilt, and decentration. The method has been tested in an artificial model with and without water, and shows accuracies similar to those of standard Purkinje imaging methods. The proposed methodology shares analysis with the standard Purkinje-based method, where pupil conjugate images are retrieved by the use of CCD camera provided with a telecentric lens. However, the availability of tomographic data from OCT allows identifying unequivocally the corresponding ocular surface producing the reflection, with no limitations arising from potential overlapping of the Purkinje images (one of the main drawbacks of the standard method). The dense lateral sampling of our spectral OCT configuration prevents the limitations produced by sparse meridional sampling (such as that used in Scheimpflug instruments). Besides, the availability of geometrical and biometrical information (corneal keratometry, lens phakometry, anterior chamber depth), required in the Purkinje method and normally gathered from different other instruments in the standard Purkinje approach, can be retrieved from the same 3-D OCT dataset. Despite the high acquisition rates of the OCT system the collection of 3-D en face OCT images in our current configuration is significantly slower (0.72 s) than the Purkinje method with a standard CCD camera (30 Hz), which imposes limitations to the dynamic measurement of IOL tilt and decentration, which may be of interest in some applications.30 High acquisition rates are important to avoid potential limitations imposed by eye motions. However, it is conceivable to limit the acquisition of OCT 2-D cross sections in selected regions, which would considerably diminish acquisition times. We have compared the tilts and decentrations measured directly from fan/optical distortion-corrected OCT images with those obtained from the en face OCT Purkinje-like method, and found, in general, high agreement between the data, particularly for tilt. We have identified slight differences in the definition of the pupillary axis as a potential source of the discrepancies. However, using the appropriate references in a computer eye model should result in the description of the same eye. Measurements of tilt and decentration of IOLs, along with the biometrical and anatomical parameters are of great value to evaluate optical quality in patients after cataract surgery, and to provide understanding of their relative role in optical degradation. Furthermore, measurements of IOL tilt and decentration in patients will help to optimize IOL and haptic design. Tilt and decentration are therefore critical parameters when building customized computer eye models that can predict optical performance of IOLs (Refs. 5 and 31). The quantitative 3-D anatomical information provided by OCT allows building these eye models with all geometrical and biometrical information obtained from a single instrument. Anterior 3-D OCT images allow direct estimation of IOL tilt and decentration, but the analysis requires correction of both fan and optical distortion.20 However, the Purkinje method only requires knowledge of axial biometry, anterior corneal radius of curvature, and IOL radii of curvature, easily accessible following fan distortion correction of the images and from geometrical data of the IOL. The amounts of tilt and decentration found in this study ( and , respectively) are comparable with those found in the prior literature ( and in Ref. 1; and in Ref. 32; and and in Ref. 33) in eyes implanted with standard monofocal IOLs. However, the lack of clear symmetry between right and left eyes, and particularly, the large tilts found in some eyes (i.e., S#3 OD) are likely associated with the fact that A-IOLs with hinged haptics may experience larger misalignments than standard monofocal IOLs (Ref. 4), among others due to asymmetric fibrosis in the haptic region (-syndrome in Crystalens).34 In summary, robust measurements of IOL tilt and decentration can be obtained from a Purkinje-like based analysis on a volumetric set of OCT anterior segment data. OCT-based corneal topography data along with those IOL alignment and eye rotation data from the Purkinje method and IOL geometry can be used in customized pseudophakic eye models allowing estimates of the optical quality and the factors contributing to optical degradation in these eyes. The Purkinje-like method allowed characterization of the eye rotation, lens tilt, and decentration, giving insights on the performance of implanted accommodative IOLs. These data, along with the biometrical data obtained from OCT, can be easily transferred into computer eye models for the evaluation of the contributed factors to optical degradation in eyes implanted with IOLs and the impact of IOL misalignment in particular. AcknowledgmentsThis study has been funded by Spanish Government Grant No. FIS2011-25637 and European Research Council ERC-2011 AdG-294099 “Bio-inspired optical correction of presbyopia” to S. Marcos, and Marie Curie Actions-Networks of Initial Training (ITN) FP7-PEOPLE-2010-ITN 264605 (OpAL-Optical and adaptational limits of vision). The authors acknowledge the collaborative agreement “Unidad Asociada Tecnología e Innovación sanitaria en Oftalmología” (IIS FundaciónJiménezDíaz/ IO-CSIC). ReferencesA. de CastroP. RosalesS. Marcos,
“Tilt and decentration of intraocular lenses in vivo from Purkinje and Scheimpflug imaging: validation study,”
J. Cataract. Refract. Surg., 33
(3), 418
–429
(2007). http://dx.doi.org/10.1016/j.jcrs.2006.10.054 JCSUEV 0886-3350 Google Scholar
D. A. Atchison,
“Design of aspheric intraocular lenses,”
Ophthalmic Physiol. Opt., 11
(2), 137
–146
(1991). http://dx.doi.org/10.1111/opo.1991.11.issue-2 OPOPD5 0275-5408 Google Scholar
R. Menapaceet al.,
“Accommodating intraocular lenses: a critical review of present and future concepts,”
Graefe’s Arch. Clin. Exp. Ophthalmol., 245
(4), 473
–489
(2007). http://dx.doi.org/10.1007/s00417-006-0391-6 GACODL 0721-832X Google Scholar
S. Marcoset al.,
“Three-dimensional evaluation of accommodating intraocular lens shift and alignment in vivo,”
Ophthalmology,
(2013). OPANEW 0743-751X Google Scholar
P. RosalesS. Marcos,
“Customized computer models of eyes with intraocular lenses,”
Opt. Express, 15
(5), 2204
–2218
(2007). http://dx.doi.org/10.1364/OE.15.002204 OPEXFF 1094-4087 Google Scholar
P. Rosaleset al.,
“Changes in crystalline lens radii of curvature and lens tilt and decentration during dynamic accommodation in rhesus monkeys,”
J. Vis., 8
(1), 18.1
–18.12
(2008). http://dx.doi.org/10.1167/8.1.18 1534-7362 Google Scholar
P. Phillipset al.,
“Measurement of intraocular lens decentration and tilt in vivo,”
J. Cataract. Refract. Surg., 14
(2), 129
–135
(1988). http://dx.doi.org/10.1016/S0886-3350(88)80086-5 JCSUEV 0886-3350 Google Scholar
J. C. BarryM. DunneT. Kirschkamp,
“Phakometric measurement of ocular surface radius of curvature and alignment: evaluation of method with physical model eyes,”
Ophthalmic Physiol. Opt., 21
(6), 450
–460
(2001). http://dx.doi.org/10.1046/j.1475-1313.2001.00612.x OPOPD5 0275-5408 Google Scholar
P. RosalesS. Marcos,
“Phakometry and lens tilt and decentration using a custom-developed Purkinje imaging apparatus: validation and measurements,”
J. Opt. Soc. Am. A, 23
(3), 509
–520
(2006). http://dx.doi.org/10.1364/JOSAA.23.000509 JOAOD6 0740-3232 Google Scholar
M. C. Dunneet al.,
“Non-invasive phakometric measurement of corneal and crystalline lens alignment in human eyes,”
Ophthalmic Physiol. Opt., 25
(2), 143
–152
(2005). http://dx.doi.org/10.1111/opo.2005.25.issue-2 OPOPD5 0275-5408 Google Scholar
T. KirschkampM. DunneJ. C. Barry,
“Phakometric measurement of ocular surface radii of curvature, axial separations and alignment in relaxed and accommodated human eyes,”
Ophthalmic Physiol. Opt., 24
(2), 65
–73
(2004). http://dx.doi.org/10.1046/j.1475-1313.2003.00168.x OPOPD5 0275-5408 Google Scholar
P. Rosaleset al.,
“Crystalline lens radii of curvature from Purkinje and Scheimpflug imaging,”
J. Vis., 6
(10), 1057
–1067
(2006). http://dx.doi.org/10.1167/6.10.5 1534-7362 Google Scholar
D. O. MuttiK. ZadnikA. J. Adams,
“A video technique for phakometry of the human crystalline lens,”
Invest. Ophthalmol. Vis. Sci., 33
(5), 1771
–1782
(1992). IOVSDA 0146-0404 Google Scholar
Y. Nishiet al.,
“Reproducibility of intraocular lens decentration and tilt measurement using a clinical Purkinje meter,”
J. Cataract. Refract. Surg., 36
(9), 1529
–1535
(2010). http://dx.doi.org/10.1016/j.jcrs.2010.03.043 JCSUEV 0886-3350 Google Scholar
S. Marcoset al.,
“Balance of corneal horizontal coma by internal optics in eyes with intraocular artificial lenses: evidence of a passive mechanism,”
Vision Res., 48
(1), 70
–79
(2008). http://dx.doi.org/10.1016/j.visres.2007.10.016 VISRAM 0042-6989 Google Scholar
P. Rosaleset al.,
“Intraocular lens alignment from Purkinje and Scheimpflug imaging,”
Clin. Exp. Optometry, 93
(6), 400
–408
(2010). http://dx.doi.org/10.1111/j.1444-0938.2010.00514.x 0816-4622 Google Scholar
J. Taberneroet al.,
“Instrument for measuring the misalignments of ocular surfaces,”
Opt. Express, 14
(22), 10945
–10956
(2006). http://dx.doi.org/10.1364/OE.14.010945 OPEXFF 1094-4087 Google Scholar
J. E. CoppensT. J. van den BergC. J. Budo,
“Biometry of phakic intraocular lens using Scheimpflug photography,”
J. Cataract. Refract. Surg., 31
(10), 1904
–1914
(2005). http://dx.doi.org/10.1016/j.jcrs.2005.03.078 JCSUEV 0886-3350 Google Scholar
S. Ortizet al.,
“Full OCT anterior segment biometry: an application in cataract surgery,”
Biomed. Opt. Express, 4
(3), 387
–396
(2013). http://dx.doi.org/10.1364/BOE.4.000387 BOEICL 2156-7085 Google Scholar
S. Ortizet al.,
“Optical distortion correction in optical coherence tomography for quantitative ocular anterior segment by three-dimensional imaging,”
Opt. Express, 18
(3), 2782
–2796
(2010). http://dx.doi.org/10.1364/OE.18.002782 OPEXFF 1094-4087 Google Scholar
S. Ortizet al.,
“Corneal topography from spectral optical coherence tomography (sOCT),”
Biomed. Opt. Express, 2
(12), 3232
–3247
(2011). http://dx.doi.org/10.1364/BOE.2.003232 BOEICL 2156-7085 Google Scholar
S. Ortizet al.,
“In vivo human crystalline lens topography,”
Biomed. Opt. Express, 3
(10), 2471
–2488
(2012). http://dx.doi.org/10.1364/BOE.3.002471 BOEICL 2156-7085 Google Scholar
X. Wanget al.,
“IOL tilt and decentration estimation from 3 dimensional reconstruction of OCT image,”
PLoS One, 8
(3), e59109
(2013). http://dx.doi.org/10.1371/journal.pone.0059109 1932-6203 Google Scholar
L. Liet al.,
“Research on calculation of the IOL tilt and decentration based on surface fitting,”
Comput. Math. Methods Med., 2013 572530
(2013). http://dx.doi.org/10.1155/2013/572530 1748-670X Google Scholar
S. Ortizet al.,
“Quantitative OCT-based corneal topography in keratoconus with intracorneal ring segments,”
Biomed. Opt. Express, 3
(5), 814
–824
(2012). http://dx.doi.org/10.1364/BOE.3.000814 BOEICL 2156-7085 Google Scholar
I. Grulkowskiet al.,
“Anterior segment imaging with Spectral OCT system using a high-speed CMOS camera,”
Opt. Express, 17
(6), 4842
–4858
(2009). http://dx.doi.org/10.1364/OE.17.004842 OPEXFF 1094-4087 Google Scholar
A. Perez-EscuderoC. DorronsoroS. Marcos,
“Correlation between radius and asphericity in surfaces fitted by conics,”
J. Opt. Soc. Am. A, 27
(7), 1541
–1548
(2010). http://dx.doi.org/10.1364/JOSAA.27.001541 JOAOD6 0740-3232 Google Scholar
S. Ortizet al.,
“Three-dimensional ray tracing on Delaunay-based reconstructed surfaces,”
Appl. Opt., 48
(20), 3886
–3893
(2009). http://dx.doi.org/10.1364/AO.48.003886 APOPAI 0003-6935 Google Scholar
S. Ortizet al.,
“Optical coherence tomography for quantitative surface topography,”
Appl. Opt., 48
(35), 6708
–6715
(2009). http://dx.doi.org/10.1364/AO.48.006708 APOPAI 0003-6935 Google Scholar
J. Taberneroet al.,
“Determining the stability of implanted Iols with a dynamic purkinje-meter system,”
Invest. Ophthalmol. Vis. Sci., 53
(2012). IOVSDA 0146-0404 Google Scholar
J. Taberneroet al.,
“Predicting the optical performance of eyes implanted with IOLs to correct spherical aberration,”
Invest. Ophthalmol. Vis. Sci., 47
(10), 4651
–4658
(2006). http://dx.doi.org/10.1167/iovs.06-0444 IOVSDA 0146-0404 Google Scholar
M. C. Wanget al.,
“Position of poly(methyl methacrylate) and silicone intraocular lenses after phacoemulsification,”
J. Cataract. Refract. Surg., 24
(12), 1652
–1657
(1998). http://dx.doi.org/10.1016/S0886-3350(98)80359-3 JCSUEV 0886-3350 Google Scholar
J. S. KimK. H. Shyn,
“Biometry of 3 types of intraocular lenses using Scheimpflug photography,”
J. Cataract. Refract. Surg., 27
(4), 533
–536
(2001). http://dx.doi.org/10.1016/S0886-3350(00)00649-0 JCSUEV 0886-3350 Google Scholar
L. YuenW. TrattlerB. S. Boxer Wachler,
“Two cases of Z syndrome with the Crystalens after uneventful cataract surgery,”
J. Cataract. Refract. Surg., 34
(11), 1986
–1989
(2008). http://dx.doi.org/10.1016/j.jcrs.2008.05.061 JCSUEV 0886-3350 Google Scholar
BiographyMengchan Sun is currently an early stage researcher at the Instituto de Optica, Consejo Superior de Investigaciones Científicas (CSIC), which she joined in 2012 and where she works under the supervision of Prof. Susana Marcos at the Visual Optics and Biophotonics Laboratory. She is a Marie Curie Fellow of the Initial Training Network (ITN) OPAL (Optical and Adaptational Limits of Vision) funded by the European Commission’s Seventh Framework Programme (FP7) under the Marie Curie Actions. Prior to this position, she was a master’s student at the Department of Information Communication Techniques, KTH—Kungliga Tekniska Högskolan (Royal Institute of Technology) in Stockholm, Sweden. Her previous professional experience includes Optical Engineer in MECAL, Eindhoven, The Netherlands (2010) and member at the Energy Research Centre of the Netherlands (2009). |