|
|
1.IntroductionIn a recent paper from our laboratory, Apfelbaum et al.1 described optical effects to be considered when prescribing prisms for visual field expansion. The main effects are the loss of field at the prism apex (the apical scotoma), induced visual confusion (seeing two different views at the same apparent direction), and diplopia (seeing the same view at different apparent directions). Analyses were based on the commonly used simplification and disclaimer that prism distortions were not considered, as they are often ignored when prescribing ophthalmic prisms. In this paper, we show that these are not necessarily safe assumptions for the high prism powers and incidence angles involved in configurations used for treatments. The variability of prism power with angle of incidence and the possibility of encountering internal reflections can materially affect the intended rehabilitative effects. We analyze these conditions and identify ways to mitigate them. Homonymous hemianopia (HH) is visual field loss in both eyes on the same side and to a similar extent. It is caused by postchiasmal lesions such as stroke, tumor, or traumatic brain injury.2 The most common etiology of HH is stroke, and roughly one third of stroke patients have either HH or hemineglect.3 HH causes difficulties in detecting objects on the nonseeing (blind) side that may cause bumping into obstacles and falls, failure to see potential blindside hazards while driving,4–6 and reduced independence and quality of life.7,8 Spectacle-mounted prisms in various configurations have been proposed to expand the visual field of patients with HH, including bilateral yoked prisms, unilateral and bilateral sector prisms, and unilateral and bilateral peripheral prisms.1,9–13 When the prisms are fitted with the base toward the blind side, they shift portions of the visual scene and image objects from the patient’s blind visual field into view in the seeing field. The prism blocks a part of the intact visual field (the apical scotoma). If fitted binocularly as is the case with the bilateral sector prisms, there is no visual field expansion. Instead, part of the intact visual field is substituted with the prism view of the blind field.1 If prisms are fitted on only one carrier lens (unilaterally), actual field expansion (increase in area seen), rather than just field substitution, can be achieved, as different views are provided by each eye. Binocular visual confusion is a necessary consequence of such true field expansion with prisms.1 Prior unilateral sector prism designs (e.g., the Gottlieb lens or press-on Fresnel prism) used low-power prisms that only expanded the field by 6 to 9 deg, and only when gaze was directed into the prism mounted on the side of the lens corresponding to the blind hemifield.1 A different approach to fitting prisms for HH was proposed by Peli12 and made available commercially by Chadwick Optical (Souderton, Pennsylvania) as peripheral prisms, also known as expansion prisms or Peli prisms. Peli suggested placing high-power press-on Fresnel prism segments across the entire peripheral portion of the lens, including both the blind and seeing hemifields.12 Unlike prior designs, this allowed field expansion in primary gaze (PG) (when field expansion is most valuable) or even when gazing away from the blind field. Later, Peli and Chadwick Optical introduced the permanent peripheral prism, composed of a conventional spectacle lens with a rigid Fresnel prism inserted into peripheral portions of the lens.14 These allowed as high as 57 prism diopters () () to be used. Placing the prisms “peripherally” (where binocular confusion and diplopia are well tolerated) avoids “central” binocular confusion and diplopia (where they are disturbing and annoying), while providing awareness in the periphery without need for scanning. The 22-mm width of the commercial prism segments extends approximately 29 deg right and left of PG, so that prism views should remain available as gaze is shifted right and left.1 However, the distortions and reflections analyzed and described here for the most commonly used configuration show that, in particular for gaze shifts toward the blind hemifield, the prism views can be severely limited. The problem is illustrated in Fig. 1. The upper half shows a calculated diagram of the image through a prism placed base left (as fitted for left HH) in front of a perimetry grid, assuming (as in Ref. 1) uniform deflection through the prism at all angles of incidence, the constant deflection angle (CDA) assumption, and not considering internal reflections. The lower half is an actual photograph of the grid through a rigid Fresnel prism. The view through the prism at the apex side is slightly magnified, whereas the view to the left is severely compressed (minified). Given the high angle of incidence at the prism apex, the prism has less than its rated (nominal) power and thus less “prism jump” at its apex (and a smaller apical scotoma) than in the upper diagram. At incidence angles greater than about 5 deg to the left of the grid center, total internal reflection (TIR) occurs. In that region, none of the “intended” view is seen, and dim reflections from unintended portions of the scene become visible. Note, however, that when the eye is at PG, the strongest reflections fall in the blind hemifield and are thus only consequential when the patient is gazing to the left. In this paper, we call the image portion seen through the prism as field expansion the intended image, and any other image portions seen through the prism are considered spurious images. Fig. 1Distortions and reflections in a base-left prism. A perimetry grid (concentric circles) was used to illustrate the prism distortion at primary gaze (PG). The upper half shows a calculated view of the grid, assuming a constant deflection angle (CDA) of 30 deg (). The lower half is a photograph taken through a Fresnel prism with its flat surface closest to the eye (camera) and with outward prism serrations (OPS). Thus, the angle of incidence at the center of the prism PG is 0 deg and the prism deflects with its rated 30-deg power. Power falls with eccentricity to the right of PG, and the image at the apex (a) is shifted only by about 20 deg. To the left of PG, power increases and transmittance of the intended image decreases rapidly with eccentricity toward the base (b), reaching TIR at about 5 deg left (red arrow). Beyond that, the intended shifted grid view is missing and spurious reflections dimly show unrelated regions of the scene (grid lines and blue blur from a window). With this photo setup, the 22-mm-wide prisms subtend about 50 deg of visual angle, not the usual 58 deg because of a difference in prism to nodal point distances of the camera and human eye. 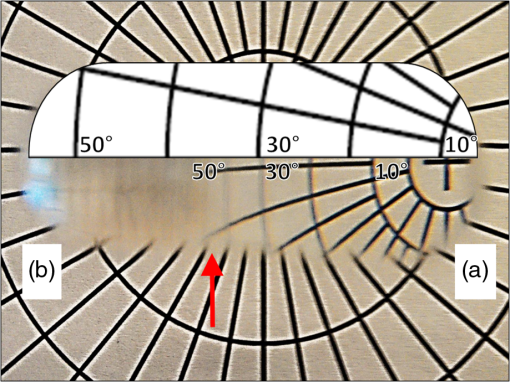 The prism in Fig. 1 is mounted as currently recommended and practiced for fitting the rigid polymethyl methacrylate (PMMA) prism inserts, with the flat surface toward the eye and the Fresnel serrations outward (outward prism serrations, OPS). If the prism is flipped so that the serrations are inward (eyeward prism serrations, EPS), the angles of incidence from the eye into the prisms are changed. Examining the optical properties of these two configurations (OPS and EPS) should lead to a better understanding of the limitations of current fitting approaches which may lead to modifications to the way prisms are applied or improved prism designs. Interestingly, flexible Press-On™ Fresnel prisms (3M, St. Paul, MN) are generally placed on the inner surface of the carrier lens, to protect them from dust and UV exposure that causes deterioration, so the effects noted while using them during a trial period in an EPS configuration are not the same as those encountered when fitting the permanent rigid prisms (in OPS configuration). The analyses below examine only the OPS and EPS configurations for rigid PMMA prisms. 2.PrinciplesThe optics of prism distortions and reflections are well established in the literature,15–22 and we offer no new characterizations here. In this section, we briefly summarize the impact of these effects on the use of high-power peripheral prisms for HH and identify the notations used in the remainder of this paper. 2.1.NotationsFigure 2 illustrates the angle notations and sign conventions we use. Although we are interested in rays of light coming from the environment into the eye, it is easier to illustrate with rays that emerge from the eye’s nodal point (NP) and progress through the prisms, as shown in Fig. 2. The principle of optical reversibility makes this acceptable. For the prism fittings used in the examples below, the distance from NP to the first refracting surface of the prism at PG is assumed to be 20.1 mm, as in Ref. 1. The prisms in this paper are always mounted base left, as would be fitted for left HH. Thus, the angle from PG to the prism apex () is for a 22-mm-wide prism fitted so that it is laterally centered on the pupil, as is the clinical protocol.1 For simplicity, we ignore any effects of vertical prism offset, as they do not materially affect the main conclusions, though they do result in additional prism distortion effects.16,22 Fig. 2Notations. NP is the nodal point of the eye. It is convenient to trace rays from NP out, rather than in the direction light travels. The angle sign convention is that clockwise rotation from the normal to the surface is positive, as illustrated in the circle. The prism apex angle is . PG is the PG direction (the head direction). is the angle of rotation of the first refracting surface from the normal to PG. for OPS and for EPS. When we describe a shifted image viewed through the prism, gaze direction and retinal eccentricity have to be considered. Although the deflection at the gaze point is determined by the angle of incidence at the gaze point, the deflection angle () at each other retinal eccentricity () depends on the angle of incidence at that eccentricity. The figure illustrates a gaze shifted left from PG to an arbitrary (and negative) gaze angle . The retinal eccentricity of the ray shown in red is , while its angle from PG is (so ). is the resulting angle of incidence of the ray at the first refracting surface. . An angle of incidence at the first refracting surface results in prism deflection angle relative to and visual angle relative to PG. The deflection angle and visual angle at the apex edge are determined by the angle of incidence at the apex. As explained later, we measure gaze angles from NP, not the eye’s center of rotation. 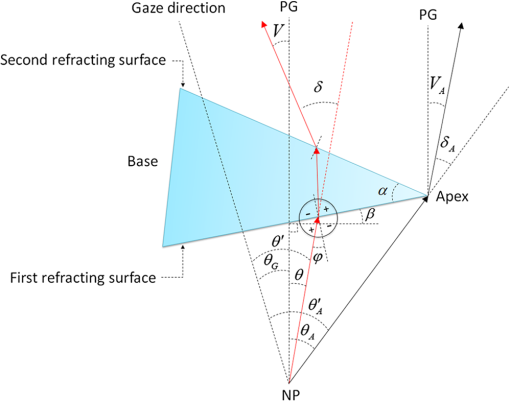 The direction of the intended image seen through the prism depends on the gaze direction () and relative retinal eccentricity () in view. Although the intended image through the prism is perceived at retinal eccentricities measured from the gaze direction (), the angle of incidence () and the deflected visual angle () are determined by the eccentricity from PG (). Deflection angle at a particular gaze direction () is used for discussing variations in prism power by angle of incidence. Deflection angle at a specific retinal eccentricity () in a particular gaze direction () is used for discussing effects of image distortion such as magnification and minification. 2.2.DeflectionThe deflection of a ray with the incidence angle through a prism with the index of refraction relative to air and apex angle is Equation (1)17,18 was used to generate the deflections in Fig. 3. If the angle of incidence, , is zero, the deflection is Fig. 3Prism power (left axis) and light transmittance (right axis) as a function of angle of incidence calculated for and prisms. The higher-power prism () varies in deflection and transmittance substantially more than the lower-power prism (). For an OPS prism, gaze angle () and incidence angle at the gaze point are the same, so the deflection angle also represents the expansion angle at the gaze angle. With the expansion saturates at the point of TIR beyond an incidence angle of . 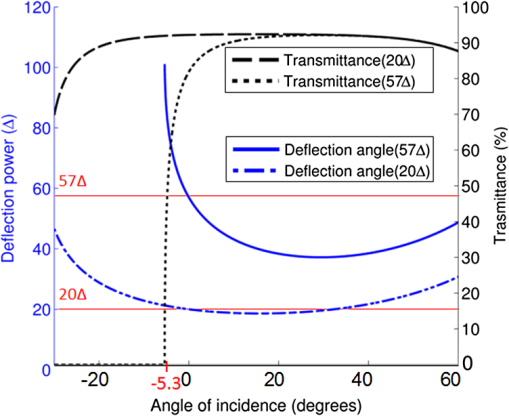 This nominal power, when expressed in prism diopters (), is usually taken as the rated prism power : Thus, a PMMA prism with index of refraction 1.49 and apex angle 38.6 deg has power of . Minimum deflection through the prism occurs when . Thus, a prism has a minimum deflection of 20.4 deg () at an incidence angle of 29.5 deg, which is very close to the prism apex. (In some cases, the minimum power is considered the rated power).22 TIR first occurs at the critical angle of incidence : therefore, a PMMA prism has a critical incidence angle of .Figure 3 plots the effective prism power (deflection expressed in prism diopters) as a function of angle of incidence () for a prism (solid blue line). The plot for a prism is also shown for comparison (dot-dashed blue line), illustrating that the CDA assumption is a reasonable approximation over a wide range of relevant angles of incidence for the moderate power, but not the high power. 2.3.ReflectionsIn addition to refraction, some reflection occurs at each optical surface.19 When the ray passes through the prism, a portion of light is transmitted and a portion is reflected at each surface. Although slight reflections from the first refracting surface can be seen, that path is usually blocked by the facial structures in the peripheral prism case. At the first refracting surface, we only consider the percent loss of transmittance. At the second refracting surface, the transmitted portion is the ray deflected by the prism and transmittance depends highly on the angle of incidence at the surface.19 We consider both transmitted and reflected light at the second surface. Figure 3 includes curves for the total percent transmittance of the and PMMA prisms. Light reflected at the second refracting surface can reach the eye and be perceived. As the transmittance is reduced (at incidence angles close to the critical incidence angle), the brightness of the reflected rays increases and can cause unwanted artifacts. Figure 4 illustrates the various types of reflections that reach the eye and the notation we use to categorize them. The details of these effects are discussed in Sec. 3.3. Fig. 4Categories of reflections in prisms. (a) TIRs. T: Primary rays that encounter TIR at the second surface due to angle of incidence at the first refracting surface. R: primary rays that encounter TIR at the prism base. (b) Surface reflection. I: Intended path of deflected primary rays. SR: surface reflection component of transmitted primary rays. T, R, and SR are spurious reflections. 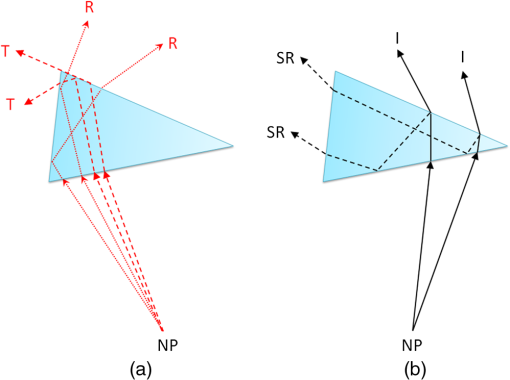 3.OPS and EPS Fresnel PrismsThe difference between OPS and EPS prisms for HH is mostly in the change in incidence angle at the first refracting surface. Since the prisms are flipped, not rotated, the prism bases remain perpendicular to the flat (nonserrated) face. The base orientation relative to the first refracting surface orientation has a significant effect on reflections. The notations for these angles are given in the caption of Fig. 2. Figure 5 shows the deflection power at the direction of gaze () as a function of gaze angle (), which, for EPS, shifts the deflection curve shown in Fig. 3 to the left. Note that the OPS configuration provides higher deflection and therefore wider field expansion around PG, with the expansion bounded by the TIR at a gaze direction of . EPS enables a shifted image for gaze directions further into the blind left field when compared to OPS. Yet, the blind-side field expansion of OPS remains wider than EPS for most of the practical gaze shift.23,24 The lower deflection angle of EPS provides the expansion at higher gaze scanning angles with less minification (compression), which may aid in hazard detection, as discussed in Sec. 3.2. However, the higher deflection angle of EPS on the seeing side results in a larger apical scotoma for this design, as shown in Fig. 6. Fig. 5Deflection power as a function of direction of gaze for prisms. The curve for the EPS prism is shifted left with respect to OPS by the size of the apex angle (38.6 deg). At the primary position of gaze the power of OPS is same as the rated power (), but the power of EPS is only . The EPS shift provides useful field expansion for gaze shifts farther into the blind hemifield than the OPS configuration, where the expansion is limited by TIR at . 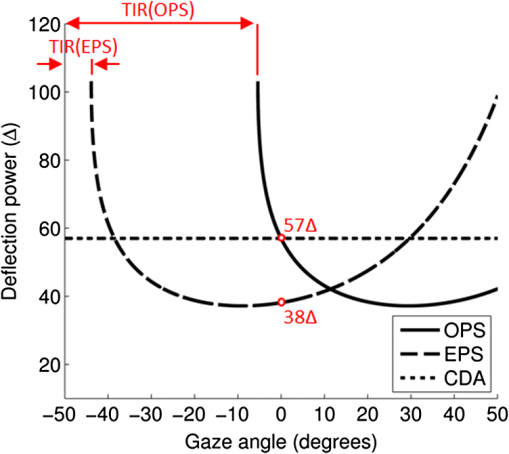 Fig. 6Apical scotoma angular size as a function of rated prism power for OPS and EPS configurations. EPS apical scotomas are slightly larger than the rated power for prisms up to . Relative scotoma size falls off considerably with increasing power in OPS configurations, becoming 10 deg smaller than the 30 deg prediction of CDA at . 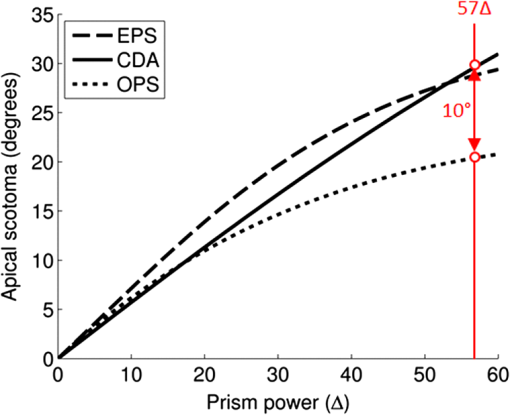 The center of rotation (CR) of the eye is assumed to be 13.5 mm behind the corneal vertex and 6.4 mm behind NP.1 Thus, the NP shifts slightly with gaze shift, and the change in angle of incidence at the prism from the NP is not identical to the angle of gaze shift. At PG, the apex of a 22-mm-wide prism is at a retinal eccentricity of 28.7 deg, while a gaze shift of only 22.5 deg is needed to gaze at the apex. However, the OPS deflection angle at the apex is 20.4 deg when seen eccentrically from PG (and 21.2 deg when the apex is viewed eccentrically from a gaze at the base), while it is 20.7 deg when the gaze is directed at the apex. For EPS, the differences in deflection angle at the apex are less than 2 deg over the full gaze range. Similarly, when at PG, OPS TIR incidence of is 1.9 mm left of PG on the prism, while it is reached with a gaze shift of 2.5 mm left of PG. These are clinically negligible differences, so all calculations below are based on the simplifying assumption that eye rotation is about NP, not CR. 3.1.Apical ScotomasThe power of a prism at its apex determines the size of the apical scotoma, the field lost between the nonprism and prism views.1 The CDA assumption is not appropriate for high-power prisms with large angles of incidence. Thus, the apical scotoma for a high-power prism (in OPS configuration) is substantially smaller than the rated prism power expressed in degrees. A smaller apical scotoma contributes to a larger field expansion effect. The power over the full range visible through the prism includes areas of effective power higher than the rated power that manifest as minification, resulting in overall larger field expansion with the prism than the CDA assumption suggests (though the expanded view is distorted). Figure 6 plots apical scotoma angular size as a function of rated prism power for OPS and EPS configurations at PG. The EPS apical scotoma does not deviate much from the rated prism power over a wide range of powers. It is actually greater than the rated power for prisms up to , dropping below the prism rating for higher powers. The OPS apical scotomas are smaller than the prism rating for prisms rated higher than , dropping by a meaningful 10 deg for . The size of the apical scotoma is an important consideration when fitting the peripheral prisms.1 3.2.Field Expansion, Substitution, or LossThe change in power with angle of incidence can be considered as a local magnification or minification ratio at each gaze point (the slope of the power versus incidence angle curve), as plotted by the dashed lines and right axes of Figs. 7(a) and 7(b). Minification results in monocular field expansion, while magnification results in monocular field loss, and the variation of power within the prism is perceived as distortion. In some fittings, monocular field loss can be partially or fully recovered in the binocular view by the fellow eye.1 The deflection at the gaze point () determines the amount of field expansion available to the patient with HH at the gaze point, as plotted by the solid curves and left axes of Figs. 7(a) and 7(b). With magnification , the field expansion is smaller than the rated prism power, and with magnification (minification), the field expansion is wider than the rated power. If, as is the case for OPS, TIR is encountered, gaze shift beyond the critical angle of incidence cannot provide farther expansion and visual retinal eccentricity for expansion saturates at the point of TIR onset, since that is the last deflected ray still visible. Fig. 7Magnification and minification with prisms. (a) OPS prism deflection visual angle () at the gaze point () varies with gaze angle (). At each gaze direction, the variable deflection (left axis) manifests as a different amount of minification (right axis). (b) With EPS, TIR is not reached within the prism segment, and there is magnification at most gaze angles. (c) Monocular field expansion (exit visual field size minus prism entrance visual field) as a function of gaze angle. OPS provides true monocular field expansion at all gaze angles into the prism, while EPS magnifies and loses monocular field area. Of course, with the angular shift, unilateral EPS provides binocular field expansion but less than OPS. (Note that for OPS, at gaze angles below TIR, the deflection at TIR remains available in the seeing hemifield, so the deflection visual angle at the critical angle of incidence is given as the deflection visual angle at the gaze point). 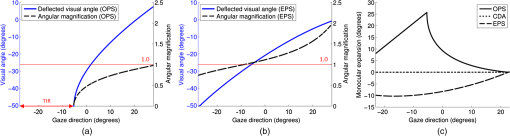 Figure 7(c) shows the monocular field expansion of prisms for HH; the difference between the exit visual field size [: the field seen between the deflected visual angle () at the gaze point () and the deflected visual angle at the apex edge ()] and the entrance visual field (: angle from the gaze point to the apex). In this situation, both the gaze angle () and the retinal eccentricity () have to be considered to determine the field expansion through the whole prism segment. If , then there is minification (magnification ) and the prism provides true monocular field expansion, while if equal, and there is simply field substitution by shifting. If magnification , there is actually a loss in monocular angle covered. Equivalently, there is expansion if . The minification at all gaze angles with OPS thus provides monocular expansion, while EPS magnifies and thus loses field width at all gaze angles into the prism. The effects of these distortions are illustrated in Fig. 8 with simulated monocular Goldmann visual field diagrams and percept diagrams, similar to those introduced in Ref. 1 for PG and for gaze directed at 5 and 20 deg to the left. Simulations were calculated in MATLAB (MathWorks, Natick, MA). Percept diagrams simulate the patient’s view through the prisms, as if the patient is viewing a perimetry grid. Here, however, the percepts include shading to represent the variation in transmittance through the prisms, an effect that was not considered previously. Fig. 8Simulated monocular Goldmann and percept diagrams for left HH to illustrate prism distortions and apical scotomas. Columns 1, 2, and 3 are for gazes at primary, and , respectively. Row (a) identifies the variation of deflected visual angle () at each retinal eccentricity (). Specifically, the retinal eccentricity to the apex () and gaze (always ) point (for primary, , and gaze direction) are marked to show the eccentricity range. Rows (b), (c), and (d) are the Goldmann diagrams and the percept diagrams for CDA, OPS, and EPS configurations, respectively. Field in the apical scotomas, hatching, would be visible in the binocular view. Differences in apical scotoma size due to prismatic magnification and minification are evident, as are the compressive effects near TIR for OPS. Since deflection angle for EPS changes slowly around PG, there is less distortion and less variation in transmittance than for OPS, as seen in the percept diagrams. However, the expanded visual field in each case for EPS is always smaller than for OPS. Only the seeing field is shown for the percept diagrams to save space. 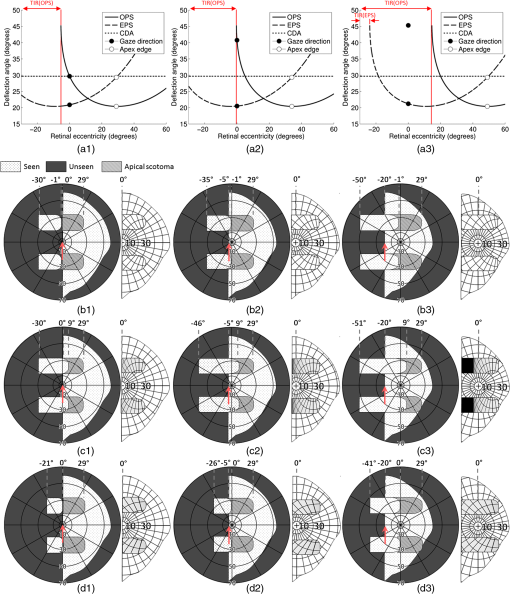 3.3.Spurious ReflectionsSusceptibility to reflections is different for the OPS and EPS configurations. Unlike the orientation difference of the first refracting surface (), the bases of the prisms remain perpendicular to the flat surface (first refracting surface for OPS and the second refracting surface for EPS). Figure 9 illustrates the relevant reflection paths. Fig. 9Spurious reflections for OPS (a and b) and EPS (c and d). T: primary rays that encounter TIR due to angle of incidence . R: primary rays that encounter TIR at the prism base. I: intended path of deflected primary rays. SR: surface reflection component resulting from reflections at either surface or both. 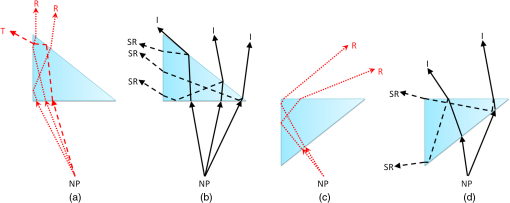 The periodic base structure of the Fresnel prisms strongly influences the spurious reflections. Using a ray tracing program (Zemax, Bellevue, Washington), we traced all incoming rays to the OPS and EPS Fresnel prisms that pass through NP and thus are imaged on the retina. This analysis identified both the source and strength (brightness) of the spurious images. In Fresnel prisms, numerous optical paths exist for reflection, transmission, and scattering of rays. However, we focus here on optical paths forming images in the eye and not those that result in nonimaging scattering and dispersion. The optical paths of imaging reflections found to be meaningful in magnitude are diagrammed in Fig. 10. Imaging reflections may cause monocular confusion if they are superimposed on parts of the intended image, and monocular diplopia or polyopia if they replicate an image of an object(s) from the intended direction but image it in another direction. Fig. 10Meaningful reflections in Fresnel prisms. (a) For OPS, primary rays at negative incidence angles reflect via TIR from the bases, causing a strong spurious (and reversed) image (R). At incidence angles , this image appears in the dark region of TIR of the intended expanded image at the second refracting surface, making it highly visible. These reflections can readily cause monocular diplopia and false alarms when the wearer scans toward the blind hemifield. Relatively dim surface reflections (SR) at the second refracting surface from primary rays at higher negative incidence angles are reflected via TIR at the first refracting surface and exit through the bases. If they originate in a region much brighter than the intended image they can cause monocular visual confusion and reduced contrast. (b) For EPS, the base reflections can be encountered over the full range of gaze angles, either as a first refracting surface or via reflection. TIR reflections (R) at the bases can form bright spurious images with monocular visual confusion and diplopia. SRs at the bases can form dim images, noticeable with monocular visual confusion and diplopia if they originate from a particularly bright region in the environment. I: intended path of deflected primary rays. 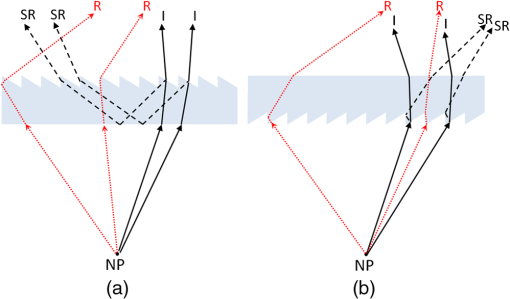 Figure 11 uses simulated monocular Goldmann diagrams to show the effects of reflections for the three gaze angles (PG, , and ), with OPS and EPS prisms. With the unilateral fit, the areas corresponding to the prism field on the seeing side in the fellow eye are also seeing, resulting in further binocular confusion and possible diplopia, as shown in Ref. 1. Fig. 11Simulated monocular Goldmann perimetry indicating field locations of sources of meaningful reflections in Fresnel prisms for left HH. (a) OPS and (b) EPS. Goldmann diagrams indicate where in the observed scene the detected stimulus would be located, not where it falls in the subject’s visual field. Areas shaded (as calculated by ray tracing) to indicate monocular diplopia or triplopia identify stimulus regions where the subject would see more than one image of the same stimulus at the same time in different directions. Seen (S) indicates both the intended view through the prism and the nonprism view. To differentiate unseen and apical scotoma, we present the apical scotoma as (A). The left column diagrams PG, while the middle and left columns are for left gaze at and , respectively. SRs are seen, but at considerably dimmer luminance, while reflections on the bases (R) are bright and seen with minimal luminance loss. In all cases, SR and R portions without monocular diplopia and triplopia cause monocular visual confusion, as they are seen in the seeing hemifield and are superimposed on the intended image. With OPS, the bright reflections R are primarily within the blind hemifield and cannot be seen at PG, but their visibility increases with gaze shifts to the left. With EPS, however, R also causes monocular visual confusion and diplopia within the seeing hemifield at PG and more positive gaze angles. 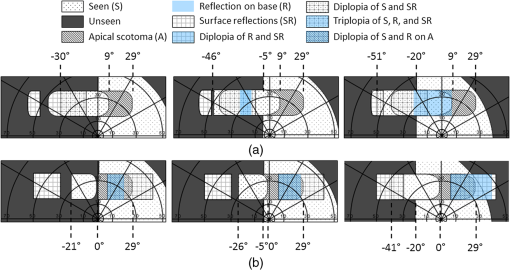 To verify the calculated predictions of Fig. 11, we conducted monocular (left eye) Goldmann perimetry of a patient with complete left HH patient, using a V4e stimulus. The results with base-left OPS and EPS prisms fitted in the conventional upper and lower locations for peripheral prisms are shown in Fig. 12. Goldmann perimetry cannot identify monocular visual confusion (since only one stimulus location is illuminated at a time). If the patient perceived only surface reflections (SR) or reflections on the base (R), they were recorded as seen areas, because the patient could not distinguish spurious and intended stimuli. The patient also did not notice reduced brightness for the SR reflections. However, the patient was asked to report (monocular) diplopia when it occurred. In addition, the patient was able to report stimulus flicker and prismatic jump, an indication of the boundary transition between different paths of stimulus reflection. This yielded considerably more information than is usually obtained with Goldmann perimetry when just detection is reported. Fig. 12Measured monocular Goldmann perimetry for the left eye of a patient with left HH. The testing was not limited to the intended prism view area, as we looked for spurious reflections. (a) OPS. The reduced extent of the apical scotoma in OPS due to the lower power at the prism apex is evident. Monocular diplopia is reported from stimuli presented in the blind hemifield where the intended image and surface reflections overlapped. The dashed vertical line indicates where the subject reported stimulus flicker, indicating a transition between distinct reflection paths, in this case due to the transition from the end of the intended expansion to the spurious reflection that caused false expansion. In actual use, the area left of diplopia causes monocular visual confusion of the intended image and the surface reflection image. (b) EPS. The reduction in apical scotoma size in this case is due to surface reflections falling on that area, causing monocular visual confusion and diplopia within the seeing hemifield, as well as the false alarms from the extreme region at the left. The seeing part at the far left of the blind left hemifield is the surface reflection portion and it may cause monocular visual confusion in actual use. 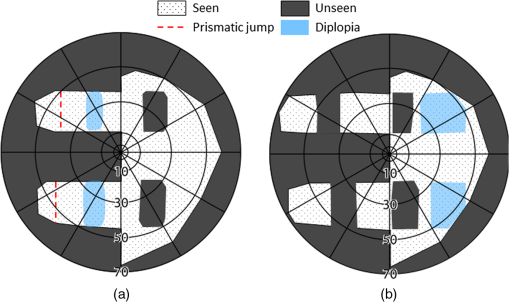 Figures 13 and 14 show photographs taken with the OPS and EPS prisms interposed. The scene, which has the institute brochure near a bright window, was selected to include bright natural sources for reflections, indicative of the disruptions that can be caused by direct sunlight or car headlights. Fig. 13Photographed view through OPS base-left Fresnel prism. The solid vertical black line in each figure is at 0 deg (PG) incidence angle and the dashed vertical line in (a), (c), and (e) is at the critical angle of incidence (). (a) The view through the OPS prism is outlined. (b) The same view without the prism. The solid outline indicates the area that would be viewed in a prism under the CDA, while the pink dashed outline indicates the area seen minified in the OPS prism in (a), illustrating the slightly smaller apical scotoma resulting from reduced power at the apex incidence and increased expansion range due to high power at the base. In (a), the white building is compressed into a blur in the intended view as TIR is approached left of prism center. (c) Reflection (R) caused by reflection on the bases is outlined (lamp and glare on the window). It is a slightly blurred mirror image of the region outlined in (d), and is seen in an area of TIR of the intended rays that only slightly reduces the contrast of the spurious reflection. Although it cannot be seen in PG with HH, it may cause monocular visual confusion and a false alarm when the gaze is shifted to the blind side. (e) Two dimmer areas of SRs are outlined and numbered (different parts of the building), and their corresponding sources are indicated in (f). They fall within the seeing hemifield, where they cause monocular visual confusion (between the building area marked 2 and part of the brochure) and some monocular diplopia (of the building portion from the area marked 1 seen from SR and the highly compressed intended view to the left of it). The camera view of the prisms subtended about resulting in a somewhat smaller effect of angle of incidence than the typically subtended by peripheral prisms. However, the prism angular shifts are the same as at the normal NP distance from the prisms.  Fig. 14Photographed view through a EPS base-left Fresnel prism. The vertical line in each figure is at 0 deg (PG) incidence angle. (a) The view through an EPS prism is outlined. The entire view is less distorted than with OPS, but reflections affect both seeing and blind hemifields. (b) The same view without the prism. The solid outline indicates the area that would be viewed in a prism with CDA, whereas the dashed pink outline indicates the area seen directly in the EPS prism. Magnification results in a narrower field seen through the prism view than with CDA or the OPS shown in Fig. 13, but without the pronounced distortion and TIR light loss left of center that affects OPS. However, the entire view is compromised by bright reflections. (c) Reflections on the bases (R) superimpose a strong mirror image of the bright area (lamp and glare on the window) to the right in (d) and cause monocular visual confusion. (e) Dimmer SRs from the area marked 2 (shaded part of building) outlined in (f) superimposes an almost see-through view in the primary seeing hemifield, causing monocular visual confusion (seeing the part of the brochure and bright building at the same direction) and reduced contrast for the intended brochure view. But, the surface reflection from the area marked 1 (area around the lamp) will fall on the blind hemifield. When the patient scans leftward, the area marked 1 (including the lamp) causes monocular visual confusion with the bright building from the intended image, and the area marked 2 causes diplopia (shaded part of the building seen twice; once dim in SR and once bright in the intended image on the blind side).  3.4.Impact of Reflections on Contrast SensitivityTo estimate the impact of spurious reflections on detection performance of objects in the expanded field, we measured contrast thresholds of three normally sighted subjects through the prisms with and without a bright light as a source of reflections. The subjects wore monocular OPS permanent prism glasses with the fellow eye patched. Black tape masked the left half of the prism to simulate hemianopia, as well as all nonprism areas of the carrier lens (on the eye side of the lens). The masking tape did not affect the ability of the left half of the prism to transmit internal reflections to the seeing side. A single prism in the upper peripheral location was used. Subjects were positioned in a head and chinrest 1 m in front of a linearized CRT monitor displaying a mean luminance of as background. A stand light positioned 40 deg left of PG could not be seen directly by the subjects but could be observed only as a surface reflection at the bases of the prisms, and thus superimposed on the view of the CRT through the prism. A fixation target on the CRT placed 10 deg into the blind hemifield (so that it would easily been seen in the prism view) was presented at the start of the trials to mark the location where the Gabor patch stimuli would appear. A horizontally oriented (to limit effects of horizontal prism distortions) Gabor stimulus was used. Subjects adjusted their head/spectacle position to superimpose the reflection of the stand light over the fixation target. Four randomly interleaved 40-trial staircases varied patch contrast. Each staircase reduced contrast after two consecutive correct responses and increased it after each incorrect response. A beep signaled the start of each 1-s trial, with the patch randomly displayed in the first or second half-second time interval, followed by another beep to indicate that the subject should respond. The subject provided a two-alternative forced-choice response by pressing one of two buttons to indicate target detection during the first or second interval. Two 160-trial sessions were completed by each subject, once without the stand light and once with. Subjects were instructed to choose a button at random if the patch was not detected. Trial data were fitted through maximum likelihood estimation to a Weibull psychometric function25 to calculate a contrast detection threshold (the contrast producing correct responses on 81.6% of trials). Figure 15 shows the change in contrast threshold caused by the surface reflections for each subject. Fig. 15Contrast detection thresholds with and without surface reflections from a bright light for three normally sighted subjects viewing through a OPS Fresnel prism. Error bars indicate the bootstrapped 95% confidence interval.26 Contrast thresholds of each subject were increased (reduced contrast sensitivity) by the base surface reflections of the stand light. 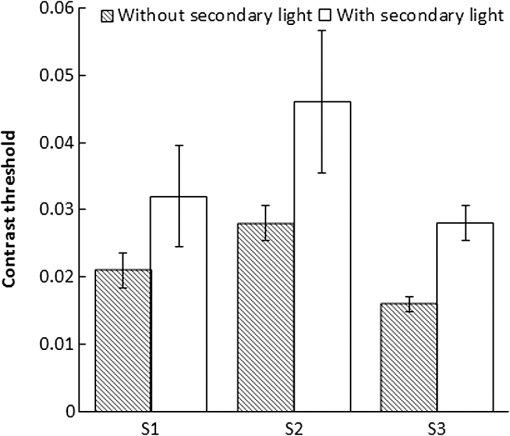 As can be seen, the addition of the surface reflections elevated the detection threshold for contrast for all subjects significantly.26 These changes in the detectable threshold of the Gabor patch contrast are attributable to the additive light effect of the spurious reflections from the secondary light. The percentage of secondary light added to the Gabor patch can be calculated as where is the contrast threshold without surface reflections and is the threshold with surface reflections, is the mean luminance of monitor, is the luminance of the reflection source, and is the fraction of the reflection source luminance transmitted as surface reflection and expressed as percentage. This calculation indicates that spurious reflections of just 1.3%, 1.6%, and 1.8% of the secondary light were seen by subjects 1, 2, and 3, respectively.4.DiscussionDistortions and reflections that have been usually ignored when prescribing prisms for field expansion are substantial and meaningful when the high-power () Fresnel prisms applied in peripheral placement are used. The current fitting of rigid prism inserts with OPS is relatively free of reflections in the seeing hemifield at PG, but rapidly encounters field compression with eventual complete loss of farther expansion due to TIR when gaze is directed toward the blind hemifield. Although scanning toward the blind side when using OPS prisms enables objects that captured attention in the prism views to be observed directly through the inter-prism lens area, it does not meaningfully increase access to peripheral field beyond that available without scanning. The current clinical fitting protocol for OPS prisms provides 30 deg of field expansion into the blind hemifield at PG. Scanning toward the blind side expands the view through the prism only up to a maximum of 5 deg of gaze shift, which expands the field by further compression up to 51 deg into the blind field. However, if a patient with HH scans beyond this point, no additional peripheral expansion will occur. Therefore, techniques proposed to train patients to scan into their blind side27 are unlikely to be synergetic with OPS peripheral prisms expansion. At least they will not increase the peripheral field expansion. The EPS configuration would be better for the application of scanning training combined with peripheral prism expansion, as with this configuration the gaze shift into the blind side will be accompanied with an increased range of peripheral field expansion. Note, however, that the combined effect at 20 deg of gaze into the blind field (about as large as can be expected23,24) will only reach 41 deg in the periphery as shown in Fig. 8(d3). That field expansion, however, will be almost free of compression and light loss and will be slightly magnified and therefore more likely to support detection of smaller or lower-contrast objects. It remains true that on scanning into the seeing side (which is more likely to occur) with either configuration, the peripheral field expansion persists with (almost) full power to the blind side, providing additional protection against the losing important view to the front when scanning into the seeing side. This is a distinct advantage of the peripheral prism over all prior designs. The interaction of field expansion with gaze direction may be particularly important in driving where scanning is critical.28 Therefore, the actual field expansion range and guidance for scanning depends on the prism configuration and should be considered when the prisms are fitted or evaluated for driving.6 The EPS configuration was used with lower power of in one driving study,6 but that was coincidental and not due to the considerations discussed here. Although the effects of prism apical scotomas can be mitigated in the binocular field with unilateral fitting, an apical scotoma equal in size to the visual angle from the PG to the apex (apex eccentricity) is optimal.1 If the apex eccentricity is greater than the size of the scotoma, binocular diplopia results at PG, as the prism image will include some of the seeing hemifield of the nonprism eye. Unlike visual confusion (which provides field expansion), diplopia has no beneficial effects. If the apex eccentricity is smaller than the apical scotoma size, the scotoma extends into the blind hemifield, where the fellow eye cannot compensate for it (at PG) resulting in a binocular scotoma that reduces the expansion effect. The prism view to the blind side of PG is subject to spurious reflections that provide little or no useful information and may cause false alarms; thus, it would make sense to truncate the prism in that region. Figure 16 plots the optimal location of the apex edge in terms of apical scotoma and the location of TIR as a function of OPS prism rated power. Our calculations suggest that the current practice of centering 22-mm-wide prisms above and below PG is suboptimal. Placing 10-mm-wide prism segments with 2 mm on the blind (base) side of PG (pupil center position) and 8 mm to the seeing (apex) side would theoretically be better. In the case of fitting , our calculations suggest 12-mm-wide prism segments with 5 mm on the blind (base) side of PG and 7 mm to the seeing (apex) side would be optimal. Such smaller prisms may also be less expensive and have better cosmetic appearance. They may also offer more flexibility in frame selection, frequently restricted by the nasal extent of the prism with the current fitting protocol. Fig. 16Optimizing OPS prism placement for PG. The prisms should not extend into the region of TIR, as that only provides spurious reflections without field expansion. The visual angle to the prism apex should equal the angular size of the apical scotoma. Extending farther into the seeing side includes field in the prism that is also seen by the fellow nonprism eye (diplopia), while the apical scotoma of a narrower prism would extend into the blind hemifield, without compensation by the fellow eye (binocular scotoma, reduced field expansion). The dotted lines indicate the current placement of 22-mm-wide prisms centered at PG. A 10-mm-wide prism with base 2 mm into the blind side of PG is optimal. 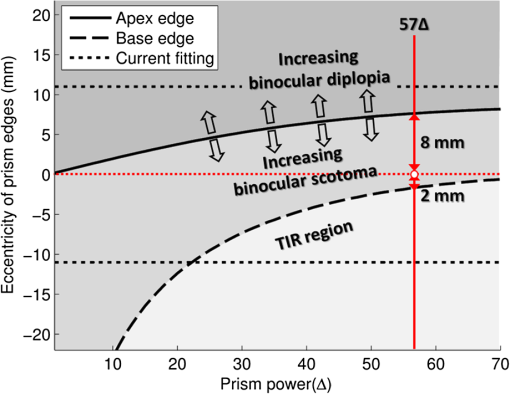 With the EPS configuration, the extremes of distortion and TIR are avoided over the gaze range of interest, although with less expansion than provided by the OPS prisms. However, our results show that EPS prisms are more prone to spurious reflections in the seeing hemifield at PG (and all other gaze directions). Still, they may be worth considering if the ability to support gaze scanning toward the blind side is desired. Though the total gain in field expansion with EPS combined with eye scanning is modest, it also comes with less minification and thus may support better detection. However, that benefit will only be realized during scanning. The ability of patients to scan and gain this benefit needs to be verified before considering this approach. The press-on prisms usually used in the EPS configuration are only available up to , while higher-power prisms are preferred for HH. Further mitigation of the effects of large incidence angles also occurs with press-on prisms, as the concave curvature of the carrier lens slightly reduces the resulting incidence angles.16 To increase the deflection power of the EPS configuration at PG a higher-power prism can be used. For example, the apex angle of a PMMA prism has to be increased to 51 deg to increase the deflection power of EPS configuration to . However, such a prism cannot be used for OPS configuration due to the TIR at normal incidence. In fact its power cannot even be specified by our definition of rated power. In addition, even with unilateral fit in EPS configuration, a binocular apical scotoma would be caused by the increased prism power at the apex edge reducing the benefit of such design. We have only discussed and analyzed the horizontal peripheral prism configuration.12,29 We did not address the oblique configuration.1,30,31 However, the same rules will apply. The horizontal component of the oblique prism can be calculated and the impact of various considerations can be determined based on the horizontal prism rated power, as shown in the various graphs included here. The vertical component is usually of low power (about ) and, therefore, many of the effects discussed here are small and inconsequential in that direction. Under usual, fairly uniform, illumination conditions, the small reduction in contrast sensitivity due to spurious reflections from the surface is unlikely to be meaningful. In extreme conditions, for example, the glare from a headlight at 10 m against nighttime roadway illumination of ,32 contrast sensitivity can be reduced by a factor of 40 with just 1.2% transmittance of surface reflections. Direct sunlight may also be a source of disturbing loss of contrast due to reflection. Any reflection above the detection threshold could be a cause for some concern. However, reflections need not overwhelm the intended view to cause visual confusion and false alarms, direct imaging of a bright source in the periphery made central by the prisms is likely to be problematic. The various directions of movement of objects seen in reflections are also a problem. Other prism configurations are conceivable, although we have not analyzed them in detail. The characteristic difference between OPS and EPS configurations are caused by the different angle of rotation of the first refracting surface. The distribution of deflection power is varied by the angle of incidence and it can be controlled by the rotation of the prism. Other related configurations of field enhancing prisms will be addressed in a future paper. The most serious spurious reflections are caused at the bases of the Fresnel prism segments, which are clear and optically flat in current products. Blocking the bases with an opaque coating would eliminate the effects of surface reflection rays that enter through the base but would not eliminate the significant rays that reflect via TIR at the bases. A matte base surface would diffuse those rays. We will not speculate as to the feasibility and cost of those remedies. For now, OPS prisms with limited width are our recommended configuration for HH, and we look forward to testing them with patients to determine whether they result in subjective or objective improvements in functionality. The analyses and principles we have provided in this paper should help clinicians make their own determinations of the configurations best suited to their patients’ needs and may lead other investigators to consider other configurations. AcknowledgmentsThis work was supported in part by NIH grants R01EY12890 and R01EY023385 (EP), and the Basic Science Research Program through the National Research Foundation of Korea (NRF) funded by the Ministry of Education, Science and Technology (2012R1A6A3A03038820) (J-HJ). We thank Henry Apfelbaum for help with the manuscript, Andrew M. Haun for experimental programming help, and Michael Dupuis for help with subject tests. Dr. Peli has patent rights (assigned to Schepens Eye Research Institute) for the peripheral oblique prisms (licensed to Chadwick Optical). Aspects of this study have been presented in abstract form as: J.-H. Jung, E. Peli, “Spurious reflection effects in Fresnel prisms used for visual field expansion,” American Academy of Optometry, Seattle, 2013. ReferencesH. L. Apfelbaumet al.,
“Considering apical scotomas, confusion, and diplopia when prescribing prisms for homonymous hemianopia,”
Transl. Vision Sci. Technol., 2
(4), 2
(2013). http://dx.doi.org/10.1167/tvst.2.4.2 1932-4553 Google Scholar
X. Zhanget al.,
“Natural history of homonymous hemianopia,”
Neurology, 66
(6), 901
–905
(2006). http://dx.doi.org/10.1212/01.wnl.0000203338.54323.22 NEURAI 0028-3878 Google Scholar
P. W. RossiS. KheyfetsM. J. Reding,
“Fresnel prisms improve visual perception in stroke patients with homonymous hemianopia or unilateral visual neglect,”
Neurology, 40
(10), 1597
–1599
(1990). http://dx.doi.org/10.1212/WNL.40.10.1597 NEURAI 0028-3878 Google Scholar
A. R. Bowerset al.,
“Driving with hemianopia: 1. Detection performance in a driving simulator,”
Investig. Ophthalmol. Visual Sci., 50
(11), 5137
–5147
(2009). http://dx.doi.org/10.1167/iovs.09-3799 IOVSDA 0146-0404 Google Scholar
P. M. Bronstadet al.,
“Hazard detection by drivers with paracentral homonymous field loss: a small case series,”
J. Clin. Exp. Ophthalmol., 2011
(S5), 1
(2011). Google Scholar
A. R. BowersM. TantE. Peli,
“A pilot evaluation of on-road detection performance by drivers with hemianopia using oblique peripheral prisms,”
Stroke Res. Treat., 2012 10
(2012). http://dx.doi.org/10.1155/2012/176806 SRTTAT 2042-0056 Google Scholar
H. T. Vuet al.,
“Impact of unilateral and bilateral vision loss on quality of life,”
Br. J. Ophthalmol., 89
(3), 360
–363
(2005). http://dx.doi.org/10.1136/bjo.2004.047498 BJOPAL 0007-1161 Google Scholar
C. GallG. H. FrankeB. A. Sabel,
“Vision-related quality of life in first stroke patients with homonymous visual field defects,”
Health Qual. Life Outcomes, 8 33
(2010). 1477-7525 Google Scholar
E. Goodlaw,
“Review of low vision management of visual field defects,”
Optom. Mon., 74 363
–368
(1983). Google Scholar
J. M. Cohen,
“An overview of enhancement techniques for peripheral field loss,”
J. Am. Optom. Assoc., 64
(1), 60
–70
(1993). JAOPBD 0003-0244 Google Scholar
E. Peli,
“Field expansion for homonymous hemianopia by optically-induced peripheral exotropia,”
Optom. Vision Sci., 77
(9), 453
–464
(2000). http://dx.doi.org/10.1097/00006324-200009000-00006 OVSCET 1040-5488 Google Scholar
E. Peli,
“Treating with spectacle lenses: a novel idea!?,”
Optom. Vision Sci., 79
(9), 569
–580
(2002). http://dx.doi.org/10.1097/00006324-200209000-00008 OVSCET 1040-5488 Google Scholar
A. R. BowersK. KeeneyE. Peli,
“Community-based trial of a peripheral prism visual field expansion device for hemianopia,”
Archiv. Ophthalmol., 126
(5), 657
–664
(2008). http://dx.doi.org/10.1001/archopht.126.5.657 AROPAW 0003-9950 Google Scholar
K. Ogle,
“Distortion of the image by ophthalmic prisms,”
AMA Archiv. Ophthalmol., 47
(2), 121
–131
(1952). http://dx.doi.org/10.1001/archopht.1952.01700030126001 AAOPAF 0096-6339 Google Scholar
A. J. AdamsR. J. KapashE. Barkan,
“Visual performance and optical properties of Fresnel membrane prisms,”
Am. J. Optom. Archiv. Am. Acad. Optom., 48
(4), 289
–297
(1971). http://dx.doi.org/10.1097/00006324-197104000-00001 AJOAAX 0002-9408 Google Scholar
B. E. A. SalehM. C. Teich,
“Ray optics,”
Fundamentals of Photonics, 1
–40 Wiley, New York
(1991). Google Scholar
M. P. Keating,
“Prism,”
Geometric, Physical, and Visual Optics, 192
–197 Butterworth-Heinemann, Woburn, Massachusetts
(2002). Google Scholar
B. E. A. SalehM. C. Teich,
“Polarization and crystal optics,”
Fundamentals of Photonics, 192
–237 Wiley, New York
(1991). Google Scholar
M. W. Morgan,
“Distortions of ophthalmic prisms,”
Am. J. Optom. Archiv. Am. Acad. Optom., 40
(6), 344
–350
(1963). http://dx.doi.org/10.1097/00006324-196306000-00003 AJOAAX 0002-9408 Google Scholar
M. Katz,
“Refraction by planes, plates and prisms,”
Introduction to Geometrical Optics, 43
–51 World Scientific Publishing Company, Singapore
(2004). Google Scholar
R. S. Slotnick,
“Adaptation to curvature distortion,”
J. Exp. Psychol., 81
(3), 441
–448
(1969). http://dx.doi.org/10.1037/h0027882 JEPSAK 0022-1015 Google Scholar
A. T. BahillD. AdlerL. Stark,
“Most naturally occurring human saccades have magnitudes of 15 degrees or less,”
Invest. Ophthalmol., 14
(6), 468
–469
(1975). INOPAO 0020-9988 Google Scholar
G. LuoF. Vargas-MartinE. Peli,
“The role of peripheral vision in saccade planning: learning from people with tunnel vision,”
J. Vision, 8
(14), 1
–8
(2008). http://dx.doi.org/10.1167/8.14.25 1534-7362 Google Scholar
N. J. H. FelixA. Wichmann,
“The psychometric function: I. Fitting, sampling, and goodness of fit,”
Percept. Psychophys., 63
(8), 1293
–1313
(2001). http://dx.doi.org/10.3758/BF03194544 PEPSBJ 0031-5117 Google Scholar
N. J. H. FelixA. Wichmann,
“The psychometric function: II. Bootstrap-based confidence intervals and sampling,”
Percept. Psychophys., 63
(8), 1314
–1329
(2001). http://dx.doi.org/10.3758/BF03194545 PEPSBJ 0031-5117 Google Scholar
J. Zihl,
“Visual scanning behavior in patients with homonymous hemianopia,”
Neuropsychologia, 33
(3), 287
–303
(1995). http://dx.doi.org/10.1016/0028-3932(94)00119-A NUPSA6 0028-3932 Google Scholar
A. R. Bowerset al.,
“Driving with hemianopia: 3. Head scanning and detection at intersections in a simulator,”
Investig. Ophthalmol. Vis. Sci.,
(2013). IOVSDA 0146-0404 Google Scholar
E. C. O’Neillet al.,
“Prism therapy and visual rehabilitation in homonymous visual field loss,”
Optom. Vision Sci., 88
(2), 263
–268
(2011). http://dx.doi.org/10.1097/OPX.0b013e318205a3b8 OVSCET 1040-5488 Google Scholar
A. BowersK. KeeneyE. Peli,
“Randomized crossover clinical trial of real and sham peripheral prism glasses for hemianopia,”
JAMA Ophthalmol.,
(2013). http://dx.doi.org/10.1001/jamaophthalmol.2013.5636 JOAPB7 2168-6165 Google Scholar
A. D. HwangE. Peli,
“Development of a headlight glare simulator for a driving simulator,”
Transport. Res. Part C Emerging Technol., 32 129
–143
(2013). http://dx.doi.org/10.1016/j.trc.2012.09.003 0968-090X Google Scholar
BiographyJae-Hyun Jung is a postdoctoral fellow at the Schepens Eye Research Institute/Massachusetts Eye and Ear, and a Research Fellow in Ophthalmology at Harvard Medical School since 2012. He received his PhD degree from the School of Electrical Engineering, Seoul National University, Republic of Korea, in 2012. His principal research interests are optical engineering in low vision rehabilitation, three-dimensional display and computational photography based on integral imaging, and optical image processing. Eli Peli received BSEE and MSEE from the Technion, IIT, Haifa, Israel, and OD degree from the New England College of Optometry, Boston, Massachusetts. He is the Moakley scholar in aging eye research at the Schepens Eye Research Institute, and a professor of ophthalmology at Harvard Medical School, Boston. He is a fellow of SPIE, the American Academy of Optometry, the Optical Society of America, and the Society for Information Display. |

