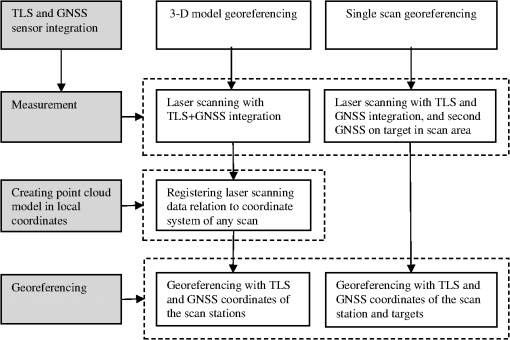
1.

Introduction

The three-dimensional (3-D) modelling of an object or surface requires high density point data ($xyz$). The 3-D model that is created depicts all details of the measured surfaces as close as possible to the real shape. Thus, 3-D models of objects and surfaces are created for various purposes such as the documentation of cultural heritage, deformation measurement, medical visualization, and urban visualization in a geographic information system (GIS). A terrestrial laser scanner (TLS) can rapidly measure a study area with a certain point separation (distance from point to point on the object). Many scans are performed to image all the details of an object and a 3-D point cloud model is created in local coordinate system by combining these scans. The created model should be registered ($\omega$, $\phi$, $\chi$ rotations and $x_o$, $y_o$, $z_o$ translations) into a geodetic coordinate system in order to allow association with other spatial data. Furthermore, spatial information technology and data management require the registration of all spatial data from different sources into a common coordinate system.

National, international, or global coordinate systems can be used as a common coordinate system. The global navigation satellite system (GNSS) is widely used for positioning and navigation purposes based on the world geodetic system established in 1984 (WGS84). On the other hand, the international terrestrial reference frame (ITRF) is a global coordinate system for geodetic measurements. Registration between these coordinate systems is always possible. Georeferencing is the term given to the registration of local measurements to a geodetic coordinate system.

The methods used to register laser scanner measurements to a geodetic coordinate system can be categorized into three groups; indirect georeferencing, direct georeferencing, and surface matching.^1,2 Indirect georeferencing is conducted using control points that have coordinates on the model and geodetic system. The registration parameters (three rotations and three translations) are calculated using at least three control points. The special target placed in the measurement area or significant details that can be distinguished on the model are used as control points. In this method, the geodetic coordinates of the control points have to be measured with terrestrial methods.^2–4 Marking and measuring the control points require extra time and cost. On the other hand, more than three control points should be used to achieve high accuracy in georeferencing.

Direct georeferencing can be realized with various techniques. References 5 and 6 estimated the rotations between the axes of a laser scanner and geodetic system by mounting a telescope on the laser scanner. For the measurement, the laser scanner is set up on a point and rotated to the direction of another point using the telescope. For this technique, the coordinates of the laser scanning station and the observed point must be known and this restricts the application of this method. Another technique for direct georeferencing is the use of GNSS or a compass with the laser scanner.^1,7–9 The GNSS receiver mounted on the laser scanner can measure the coordinates of the laser scanning station in the WGS84 datum. The rotation of the scanner is determined by the GNSS placed within the scanning area or by a compass mounted on the scanner. However, the configuration of the laser scanner, GNSS, and compass reduces the accuracy of the method. In another study, laser scanning data were georeferenced by a combination of TLS and GNSS.¹⁰ Reference 6 investigated the errors and their propagation in direct georeferenced terrestrial laser scanner networks. In addition, the reasons and effects of several systematic errors inherent to TLS datasets were presented. According to the study, the laser beam width has a significant effect on the rotation accuracy of the scan data. The usage of the TLS and GNSS combination for georeferencing is explained by Ref 11, in which was presented an autonomous way for orientation of point clouds relative to the geodetic coordinate system. Using a dual-GNSS antenna apparatus on the TLS, rotation angles have been determined with a precision of about 0.05 deg.

Georeferencing with surface matching is the registration of point clouds to the previous georeferenced point cloud dataset. Surface matching is applied with the iterative closest point (ICP),^12–14 least-square 3-D surface matching,¹⁵ or other methods.¹⁶

This paper proposes a 3-D model georeferencing and single scan georeferencing methods. Initially, the TLS and the GNSS receiver were integrated. Then the registration of the point cloud to the geodetic coordinate system was performed by the GNSS data from the continuously operating reference stations-turkey (CORS-TR) network. In the next part of the paper, Sec. 2 describes the GNSS, laser scanning, and the proposed measurement methods. The integration of the TLS and GNSS and georeferencing results are given in Sec. 3, and the discussion and conclusions are presented in Secs. 4 and 5, respectively.

2.

Materials and Methods

2.3.

Proposed Georeferencing Methods

In order to apply the georeferencing methods proposed in this study, first, a GNSS receiver was mounted on the TLS and the translations between their phase centers were estimated by calibration measurement (Fig. 1). The calibration results are used in all measurements conducted using this integration of TLS and GNSS. Two methods were proposed for georeferencing (Fig. 2):

• 3-D model georeferencing: after the point cloud model is created by the registration of all point clouds, it is registered to the geodetic coordinate system using GNSS measurements of the laser scanning stations.

• Single scan georeferencing: each point cloud is registered to the geodetic coordinate system using control points and the GNSS measurement of the laser scanning station. The control points are generated in the measurement area.

Fig. 1

Laser scanning with sensor integration of terrestrial laser scanner (TLS) and global navigation satellite system (GNSS).

Fig. 2

Point cloud registration and georeferencing with sensor integration of TLS and GNSS.

3.

Results

3.1.

Sensor Integration of Terrestrial Laser Scanner and Global Navigation Satellite System

The Topcon Hiper Plus GNSS receiver was mounted on the Ilris 3-D laser scanner using a special apparatus. The origin of the laser scanner coordinate system is the phase center of the device, and the axes are as follows: view direction, $+y$, right direction, $+x$ and upper direction, $+z$. The relationship between the ITRF and TLS coordinate systems is given by the 3-D Helmert similarity registration.²⁸

Eq. (1)

$$\left[\begin{array}{c}X\\ Y\\ Z\end{array}\right]=\lambda .R_{\omega \phi \chi }.\left[\begin{array}{c}x\\ y\\ z\end{array}\right]+\left[\begin{array}{c}{x}_o\\ y_o\\ z_o\end{array}\right],$$

where $XYZ$ are the ITRF coordinates and $xyz$ are the TLS coordinates. Since the coordinates in each system are in real dimensions, the scale ($\lambda$) between the two coordinate systems is 1. $x_o$, $y_o$, $z_o$ are the coordinates of the origin of the TLS coordinate system in the ITRF96 datum 2005.0 epoch. In this equation, at least three points with known coordinates in both systems are required to solve unknown rotations ($\omega$, $\phi$, $\chi$) and translations ($x_o$, $y_o$, $z_o$). Since the rotations between coordinate axes of TLS and ITRF will change at each position of the TLS, only the translations between their coordinate axes are estimated (Fig. 3). The translations are given by

Eq. (2)

$$\left[\begin{array}{c}{x}_{O2}\\ y_{O2}\\ z_{O2}\end{array}\right]=\left[\begin{array}{c}{X}_{O2}\\ Y_{O2}\\ Z_{O2}\end{array}\right]-\left[\begin{array}{c}{x}_o\\ y_o\\ z_o\end{array}\right],$$

where, ${[x_o{y}_o{z}_o]}^{\mathrm{T}}$ and ${[X_{O2}{Y}_{O2}{Z}_{O2}]}^{\mathrm{T}}$ are the phase center coordinates of the TLS and GNSS in relation to ITRF96 datum 2005.0 epoch, respectively. ${[x_{O2}{y}_{O2}{z}_{O2}]}^{\mathrm{T}}$ are the translations between the phase center of the TLS and GNSS receiver. In other words, these are the phase center coordinates of the GNSS receiver in relation to the coordinate system of the TLS.

Fig. 3

TLS and ITRF coordinate systems and the position of GNSS receiver on the TLS and on the target sign.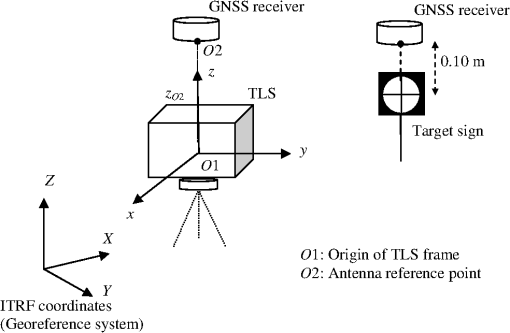

The TLS and GNSS integration was set up a random place and levelled to a horizontal plane. Another GNSS receiver placed on target shape was measured by the TLS (Fig. 3). The combination of GNSS and target sign was pointed at different locations in the measurement area keeping the position of the integrated TLS and GNSS. Laser scanning was undertaken with a 3-mm point separation (the distance between the measured points on the object) at 11 locations of the target. The GNSS data were recorded at each laser scanning station and every location of the target. Thus, the control points which have laser scanner and GNSS coordinates were constituted. The offset between the center of the target sign and the GNSS receiver placed on it was 10 cm on the vertical axis (Fig. 3). The standard deviations of the $X,Y,Z$ Cartesian coordinates measured by GNSS were 0.002, 0.001, and 0.001 m, respectively. On the other hand, the laser scanner coordinates of the control points were interactively measured from the point clouds. Here, since the $z$ axis of the coordinate systems in the integration of TLS and GNSS receiver are intersected, the translations in the direction of the $x$ and $y$ axes $(x_{O2},y_{O2})$ are zero. The translation $z_{O2}$ in the direction of the $z$ axis was estimated with 11 control points by using Eqs. (1) and (2) (Table 1).

Table 1

Coordinates of the global navigation satellite system (GNSS) receiver mounted on a laser scanner according to the coordinate system of the laser scanner (Fig. 3).

Coordinates (m)			Standard deviations (m)
$x_{O2}$	$y_{O2}$	$z_{O2}$	${\sigma }_{xO2}$	${\sigma }_{yO2}$	${\sigma }_{zO2}$
0	0	0.329	0	0	0.00514

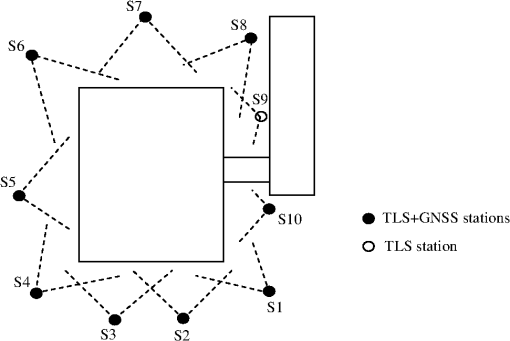
3.2.

Georeferencing

3.2.1.

Three-dimensional model georeferencing

A 3-D model of a building was created to demonstrate the application of the proposed georeferencing method. Overlapping scans were undertaken by the integration of TLS and GNSS at 10 stations with a 1-cm point separation (Fig. 4). Furthermore, check points were constituted by measuring the target joined to GNSS in the field of view.

Fig. 4

Stations on the building measurement using the integration of TLS and GNSS.

The static GNSS data were recorded for a minimum period of 7 min at each laser scanning station. The data recording period was 1 s and the satellite altitude angle was 10 deg on the measurement.

To combine the laser scanning data, the first scan was selected as a reference, and then all the others were registered to the coordinate system of this scan using ICP with PolyWorks software.²⁹ Thus, a point cloud model was generated in a local coordinate system (Fig. 5). The maximum standard deviation on registration of the point clouds was 0.009 m.

Fig. 5

Point cloud model created in a local coordinate system.

The collected GNSS data were first converted into receiver independent exchange (RINEX) format. 1-sec RINEX data of the KNYA station located in the CORS-TR were supplied to evaluate the GNSS measurement (Fig. 6).

Fig. 6

Distribution of the fixed GNSS stations in continuously operating reference stations in the network Turkey (CORS-TR).^26,30

Leica Geo Office software was used to analyze the GNSS data. The ITRF coordinates of laser scanning stations were calculated taking the offset $z_{O2}$ translation into consideration (it is 0.329 m in Table 1). On the processes of the measurements, the bases from the KNYA point in the CORS-TR network were analyzed by the GNSS receiver mounted on the Ilris laser scanning device and the target. Thus, each point was evaluated by triangles with two independent bases (Fig. 7). The analysis of the created triangle revealed that the largest triangle closure was 0.0168 m. The base measurements and loops also showed that there was no contrary measurement. The procedure continued with the adjustment of the network. In the adjustment, ITRF96 datum 2005.0 epoch coordinates of the KNYA point were taken as fixed; thus, the coordinates of all points were calculated in the ITRF96 datum 2005.0 epoch. The standard deviations of the computed points showed that the greatest values were $({\sigma }_{\varphi })\pm 0.0015\mathrm{m}$ in latitude; $({\sigma }_{\lambda })\pm 0.0011\mathrm{m}$ in longitude; and $({\sigma }_h)\pm 0.0027$ in altitude. These results indicate that the coordinates obtained from GNSS measurements were calculated with high accuracy.

Fig. 7

Calculated GNSS bases.

The ITRF and point cloud coordinates of the laser scanning stations must be known to register the 3-D model into the geodetic system. The laser scanning stations in the coordinate system of the reference point cloud were computed during the registration of point clouds. The coordinates of the check points were interactively extracted from the point cloud model. Then the point cloud model was georeferenced by a various number of control points (laser scanning stations). The accuracy was assessed with the residuals on the check points (Table 2).

Table 2

Generated three-dimensional (3-D) model georeferencing using a varying number of laser scanning stations (laser scanning was performed by the integration of TLS and GNSS).

Georeferencing			Accuracy evaluation
Control points#	TLS stations	RMSE ${\sigma }_o$ (m)	Check points#	Mean $\mathrm{d}x$ (m)	Mean $\mathrm{d}y$ (m)	Mean $\mathrm{d}z$ (m)	${\sigma }_{\mathrm{d}x}$ (m)	${\sigma }_{\mathrm{d}y}$ (m)	${\sigma }_{\mathrm{d}z}$ (m)
3	1, 5, 8	0.0500	10	$-0.0107$	$-0.0004$	$-0.0221$	0.0294	0.0157	0.0416
5	1, 3, 5, 6, 8	0.0499	10	0.0001	0.0024	$-0.0012$	0.0267	0.0152	0.0234
9	1, 2, 3, 4, 5, 6, 7, 8, 10	0.0585	10	0.0021	0.0068	$-0.0030$	0.0270	0.0166	0.0230

3.2.2.

Single scan georeferencing

The individual georeferencing of the data of each laser scanning requires two control points in addition to the laser scanning station. To achieve this, control points were constituted on the measurement area (Fig. 8). The points, signed by the target sign, have TLS and GNSS coordinates. In addition, the check points were constituted in the same way. The registration to the ITRF coordinate system was performed using three control points. The residuals on the check points were exploited to assess the accuracy of the registration (Table 3).

Fig. 8

Control and check points for the single scan georeferencing.

Table 3

Results of the single scan georeferencing.

Georeferencing		Accuracy evaluation
Control points#	RMSE ${\sigma }_o$ (m)	Check points#	Mean $\mathrm{d}x$ (m)	Mean $\mathrm{d}y$ (m)	Mean $\mathrm{d}z$ (m)	${\sigma }_{\mathrm{d}x}$ (m)	${\sigma }_{\mathrm{d}y}$ (m)	${\sigma }_{\mathrm{d}z}$ (m)
3	0.0500	3	0.0079	0.0154	0.0028	0.0115	0.0155	0.0149

4.

Discussions

The offset ($z_{O2}$ coordinate) between the phase centers of the integrated TLS and GNSS receivers was estimated using 11 control points; however, a higher number of control points and different techniques can be used. Sufficient accuracy was obtained in the georeferencing of the measurement by this sensor combination.

After the point cloud model was created in the local coordinate system, the model coordinates were registered to the georeference system with the 3-D model georeferencing method. The laser scanning stations (TLS+GNSS) were taken as the control points which have coordinates in both systems (ITRF and TLS). However, the GNSS signal might not be received at each station due to obstacles in the route of the satellite signals. In the experiment, the satellite signal was not received from a sufficient number of satellites at station 9. Therefore, the ITRF coordinates of this station could not be computed. The georeferencing was performed by varying the number of control points (laser scanning stations). This proved that the residuals on the check points were very small even though three control points were used (Table 2). A reason for the difference in the accuracy of georeferencing is the device drift from the horizontal plane during the laser scanning at each station. It causes a change in the direction of the $z$ axis of the laser scanner. Therefore, the offset ($z_{02}$) between the origins of TLS and GNSS changes a little. In addition, small changes occur on $x_{02}$ and $y_{02}$. Although these effects decrease the accuracy of the georeferencing, this is an insignificant effect due to the small drift.

In the single scan georeferencing method, each laser scanning measurement performed by the integration of TLS and GNSS was registered to the geodetic coordinate system using two control points constituted in the scan area. Thus, both combination and georeferencing are undertaken in one step. The residuals on the check points indicated that the method has high accuracy (Table 3).

In this study, the single scan georeferencing and 3-D model georeferencing methods have high accuracy. The single scan georeferencing method requires two control points in the scan field; thus, it needs more computation and is labor intensive. However, the 3-D model georeferencing method does not require a second GNSS receiver and a point that has ITRF coordinates. After the 3-D model is generated by the integration of TLS and the GNSS receiver in relation to the local coordinate system, it is georeferenced with the laser scanning stations without any control points. It needs scanning from three or more stations.

5.

Conclusions

Georeferencing of laser scanning data is the integration of point clouds with the other spatial data in a geodetic coordinate system. It is essential in areas of planning and visualization and for responding to spatial queries. This study presented the registration of laser scanner measurements to the geodetic coordinate system using the integration of TLS and GNSS in the CORS-TR network. The laser scanner measurements were registered to the ITRF datum with the CORS-TR station closest to the laser scanning field. The present study adopted a 3-D model georeferencing and single scan georeferencing methods. The 3-D model georeferencing method has multi scan overlapping. After the 3-D model is generated, the relation to the local coordinate system of the scan is selected as a reference, the georeferencing is performed by GNSS data of the scanning stations. However, the single scan georeferencing method requires a second GNSS receiver to create the control points. Consequently, the current study found that the proposed georefrencing methods were suitable for outdoor work and were more practical.