|
|
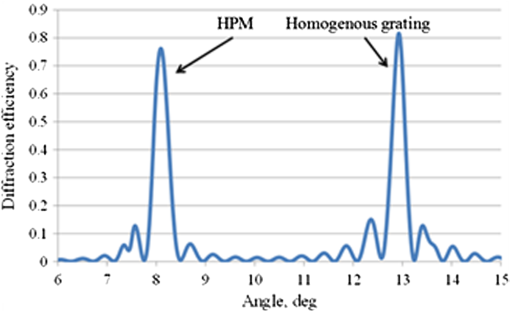
1.IntroductionOver the last decades, phase masks have found numerous applications, including imaging,1–5 encryption,6–9 beam shaping,10–14 and mode conversion.15–18 To create permanent phase masks there are two typical methods of production. The first method controls the local geometrical path length by generating a contoured surface,5,10–15 while the second method changes the local refractive index in the bulk of a photosensitive medium such as lithium niobate or photosensitive glass.19,20 Both methods can be employed to generate phase masks with almost any profile. However, because the phase shift is induced by changing the local optical path length, these phase masks are inherently limited to use at a specific wavelength, which limits the range of potential applications. To increase this range, achromatic phase masks have been previously produced utilizing either birefringent materials or the birefringence in diffraction gratings with periods below the working wavelength.21,22 Other techniques include wavelength multiplexing several computer-generated holograms so that arbitrary wavefronts can be generated when illuminated by the appropriate wavelength beam.23–25 This technique will allow the diffracted beam to have the same wavefront for multiple incident wavelengths, but requires that a separate hologram be recorded for each desired wavelength. Therefore, to make this a truly achromatic device, many holograms must be recorded and the diffraction efficiency of each hologram will necessarily be reduced. We demonstrate here that such a complex method for achromatization is unnecessary for certain phase profiles. Instead, a quasiachromatic element can be generated by encoding stepped phase mask profiles into transmitting volume Bragg gratings (TBGs),26,27 which produce holographic phase masks (HPMs). Though this technique has been demonstrated for HPMs utilized at reconstruction wavelengths identical to the recording wavelength,28,29 we show here that HPMs can produce identical diffracted phase profiles over a wide range of wavelengths as long as the Bragg condition of the volume grating is satisfied. This is in contrast to more complex holograms that, though they can be read at any wavelength satisfying the Bragg condition, cannot generally reconstruct the same phase profile at wavelengths different than the recording one. To simplify fabrication and to provide a clear demonstration of the phenomenon, we chose to use binary phase profiles, but the approach is fully applicable for multilevel phase masks as well. The HPM utilizes the diffraction characteristics of TBGs, which can diffract up to 100% of a beam into a single order and can diffract over a broad range of wavelengths by changing the angle of incidence (with the diffraction efficiency depending on the wavelength and strength of the grating).26 The high-angular selectivity of a TBG also allows for several TBGs to be multiplexed into the same element with little to no cross-talk between gratings; each grating is accessed by altering the beam’s angle of incidence onto the element. In order to explain the unique properties of the HPMs, we note that a Bragg grating is the simplest volume hologram, which, unlike more complex holograms, can, by changing the incident angle, diffract a different wavelength without distorting the beam profile. By encoding phase levels which cover a macroscopic area, the HPM acts locally as a standard TBG with a given phase shift. Thus, the HPM will diffract in the same manner as a standard TBG except at the relatively small number of phase discontinuities, and the diffracted beam’s phase profile will match the encoded phase level profile regardless of incident wavelength. The HPM, therefore, acts as a spectrally addressable phase mask, and by applying surface gratings with double the period of the HPM, a truly achromatic element will be created.30 In this paper, we focus exclusively on the properties of the HPM itself, and demonstrate HPMs that, though recorded at 325 nm, preserve a binary phase profile in the diffracted beam at wavelengths beyond and can operate over a bandwidth larger than 500 nm. These elements are used to perform fiber mode conversion and simultaneous TEM mode conversion and spectral beam combining. 2.Theory of HPM Encoding and OperationTo encode the phase profile into a TBG, consider the holographic recording setup in Fig. 1. Here, a multilevel phase mask has been placed into one arm of a two-beam interference system (the object beam), where the two beams interfere at an angle relative to the normal of the holographic sample. The two-beam interference equation describing the fringe pattern in the sample is then where is the intensity, is the wavevector for each beam, and is the phase variation introduced by the phase mask after the object beam has propagated to the sample. Since the phase mask’s profile is located in the plane, which is rotated with respect to the sample plane, the recorded phase profile will generally be different than the phase mask. However, if the thickness of the sample, the axial distance between the phase mask and the sample, and are small then , so the phase profile recorded in the hologram will be approximately the same as that of the original phase mask. The recorded hologram will have a refractive index profile of where is the background refractive index, is the refractive index modulation, and is the grating vector.Fig. 1The phase profile of a standard binary phase mask in the object beam is encoded into a volume Bragg grating at a recording wavelength of 325 nm. 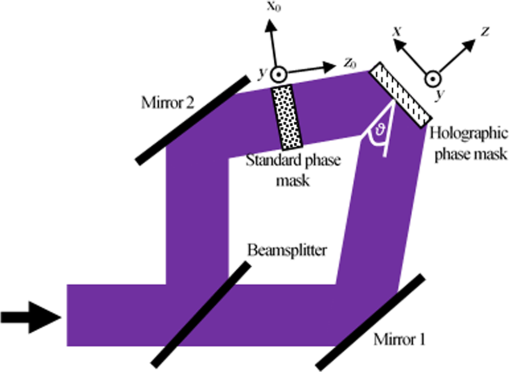 Once the hologram is recorded, it is placed in a system with some probe beam to be diffracted which may or may not have the same wavelength as the recording beams. If the probe beam is incident at or near the Bragg condition (see Kogelnik26), the total electric field will satisfy the scalar Helmholtz wave equation, Here, is the wavenumber of the probe beam. For thick volume gratings, where only a single incident and diffracted beam contain significant energy, the Helmholtz equation has a solution of the form26 where and are the complex amplitudes of the transmitted and diffracted waves, respectively, and is the wavevector of the diffracted beam. Insertion of Eq. (4) into Eq. (3) results in a set of coupled wave equations between the amplitudes and . Kogelnik26 has solved these equations when and depend solely on the axial distance (homogenous gratings). However, when a phase mask is placed in the recording system, the phase term is not a constant across the entire hologram aperture and consequently it cannot be assumed that this one-dimensional dependence will still hold. In this particular study, we are only interested in probe beams that exactly satisfy the Bragg condition. In this case, the coupled wave equations become Here, is the coupling coefficient of the grating. Note that we have assumed that the second derivatives are negligibly small in the same manner as Kogelnik,26 as we still expect the transfer of energy between the transmitted and diffracted waves to be slow.We solve the coupled equations numerically by converting Eq. (4) into Fourier space along the transverse dimensions and , giving where and are the Fourier transforms of and , respectively, and and are the spatial frequencies along the and axes, respectively. To solve these equations, we split the propagation and energy transfer between the waves into two discrete steps and successively propagate and transfer energy between waves over several small propagation steps. To calculate the propagation of the beam, the right side of Eq. (6) is assumed to be zero. In this case, the Fourier amplitudes will have a solution of the form Note that this is only exact in the case where the right side of Eq. (6) truly equals zero, but for small () propagation steps, this is a reasonable approximation. To account for energy transfer, we piecewise integrate the right side of Eq. (5) with the Euler method and add it to the inverse Fourier transform of Eq. (7)Calculations indicate that for a propagation step size of 100 nm, our numerical method conserves energy to within 0.01% after propagating the coupled waves through the entire system, which is sufficient for the phase profiles discussed here. Numerical simulations were performed to determine the diffracted beam phase profile and diffraction efficiency of an HPM in the case where a binary phase profile is encoded. The numerical method described previously was first applied to simulate a standard TBG with an period, a refractive index modulation of 250 ppm, and a thickness of 2 mm. The probe beam with a wavelength of 1064 nm is incident at the Bragg angle and propagates in the plane [see Fig. 2(a)]. Using a propagation step size of 100 nm, the simulated diffraction efficiency of this TBG is 99.13%, which is consistent with the peak diffraction efficiency of a homogenous TBG described by Kogelnik.26 A phase step was then introduced to the grating at a recording wavelength of 325 nm. This binary step was first introduced along the -axis, and then along the y-axis, to determine if there would be any orientation-dependent variations in diffraction efficiency or phase profile. The calculations were then repeated for two probe beams with wavelengths of 632 and 975 nm. In all cases, the grating parameters are the same but the incident angle was changed so that all beams were incident at their respective Bragg angles. Fig. 2(a) A probe beam incident at the Bragg angle is diffracted by a holographic phase mask (HPM) with a single phase dislocation along one axis. Numerical simulations results demonstrating: (b) the diffracted beam phase profile and (c) the local diffracted intensity of a plane wave for beams of different wavelength. (d) The diffraction efficiency of an HPM at 1064 nm relative to a standard transmitting volume Bragg grating as a function of beam diameter when a binary phase dislocation is encoded along the -axis. Here, the coordinate origin is the center of the front surface of the HPM. (e) The diffracted beam phase profile and (f) the local diffracted intensity when a binary phase dislocation is encoded along the -axis for beams of different wavelength. 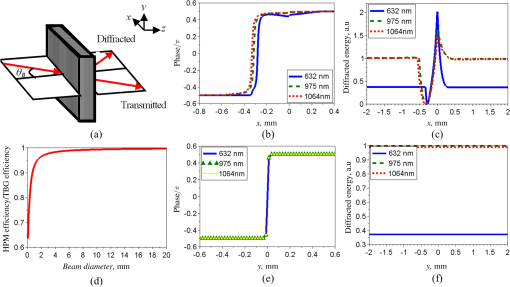 As shown in Fig. 2(b), each diffracted beam contains a phase shift when the phase step is introduced along the -axis. The location of the phase step is slightly offset from the origin due to the propagation of the beam through the sample, and changes for each beam due to their different Bragg angles. For the local intensities of the diffracted waves, shown in Fig. 2(c) for a plane wave, (note that the relative strengths are different due to the wavelength-dependent diffraction efficiency) a general decrease in diffracted energy is observed at the phase discontinuity. This is not surprising, as any region of the probe beam crossing the phase discontinuity will not be able to satisfy the Bragg condition at that point. This inability to locally satisfy the Bragg condition will result in a decrease in diffraction efficiency (which is the total energy in the diffracted beam divided by the total energy in the incident beam) that is dependent on the fraction of the beam energy which crosses the phase discontinuity. This decrease in diffraction efficiency will also mask the slight differences in phase for each wavelength in the phase transition region. However, as shown in Fig. 2(d), this loss in efficiency becomes very small with increasing beam size and the diffraction efficiency of an HPM will asymptotically approach the diffraction efficiency of a standard TBG as the beam diameter approaches infinity. When the phase discontinuity is oriented along the -axis, the phase profile of the diffracted beam will also have a phase shift, as shown in Fig. 2(e). Here, the phase discontinuity is located at the origin because the probe beam has no component propagating along the -axis. This zero -axis component results in the diffracted beam having a near zero-width transition region that is identical for every wavelength. It also results in only a single infinitesimal fraction of the beam ever encountering the phase discontinuity, giving constant local intensities for the diffracted waves, as shown in Fig. 2(f). The simulated diffraction efficiency of the HPM in this case is constantly within 0.01% of the predicted efficiency for a TBG at each wavelength as given by Kogelnik26 regardless of beam diameter, and given that there is a 0.01% uncertainty in energy conservation in the numerical method, we conclude that the diffraction efficiency is identical to a standard TBG. These two cases indicate that the diffracted beam from an HPM will always inherit the phase profile of the original phase mask, and will have some orientation-specific decrease in diffraction efficiency that is dependent on beam size and largely negligible for most typical beam diameters. Repeating these cases for other wavelengths at their respective Bragg angles show similar results, with the diffraction efficiency of both the TBG and HPM changing with respect to wavelength as described by Kogelnik.26 Thus, the HPM will maintain the diffraction characteristics of a TBG, including the wavelength and angular spectrum, while preserving the desired phase profile over the whole bandwidth of possible Bragg wavelengths. 3.Experiments3.1.HPMsA complete set of experiments have been performed using an HPM recorded in a 1.97-mm thick photo-thermo-refractive (PTR) glass sample as illustrated in Fig. 1. PTR glass is a multicomponent photosensitive glass with a transparency window from the near UV to the near IR which has the ability to sustain high power beams.31–33 It has been used in a variety of applications, including producing volume phase masks20 and holograms for pulse stretching/compression34 as well as coherent and spectral beam combining.35–37 To fabricate the HPM, a four-sector binary phase mask20 designed for the recording wavelength of 325 nm was placed in one arm of the setup and the half angle of interference was set to 0.786 deg, giving a grating period of . The phase mask was placed approximately 150 mm from the sample. In order to directly and accurately compare the diffraction efficiency of the HPM with that of a standard TBG, we fabricated a sample containing both an HPM and a homogeneous TBG in the same volume of PTR glass. This was done by recording an HPM, and then removing the phase mask from the object beam and rotating the PTR glass sample without lateral shifting to record a tilted TBG with the same recording dosage. Recording both elements in the same volume ensured that the local refractive index change and any sample inhomogeneities would be shared between the elements and demonstrated a new opportunity for holographic phase mask multiplexing. As shown in Fig. 3, the diffraction efficiencies of each element are approximately the same, showing good agreement with theoretical predictions. Note also that there is no cross-talk between the two multiplexed holograms, demonstrating that the HPM preserves the narrow angular acceptance of standard TBGs. 3.2.Mode ConversionAs demonstrated previously,20 a four-sector binary phase mask can itself be used as an optical mode converter when the probe beam center is properly aligned with respect to the phase steps. Such a binary phase mask though works only for the particular wavelength for which the phase shift is . As shown in Fig. 4(a), the expected far-field intensity profile for a beam passing through the center of a four-sector regular binary phase mask consists of a four-lobed clover pattern. However, since the phase shift is only at the design wavelength, this is the only wavelength with effective mode, as has been demonstrated by recent results for fiber modes.38 To demonstrate the capabilities of HPMs, we encoded such a four sector phase mask in a transmission volume Bragg grating, thus creating a mode converting HPM. Here, we report a series of experiments to test the theoretical predictions of the HPM multiwavelength operation presented above. If the encoded binary phase steps are indeed transferred to the probe beams diffracted from the HPM at their respective Bragg wavelengths, the HPM should simultaneously act as a diffraction element and a mode converter, when the beams are correctly aligned to the phase steps. To perform this investigation, we recorded the far-field intensity distributions of diffracted beams at multiple wavelengths by imaging them onto a CCD camera using a 500-mm lens. Fig. 4(a) Simulated far-field profile of a beam after passing through an ideal four-sector binary mask and the diffracted beam from a four-sector HPM at (b) 632.8 nm, (c) 975 nm, and (d) 1064 nm. The sizes shown here are not to scale. 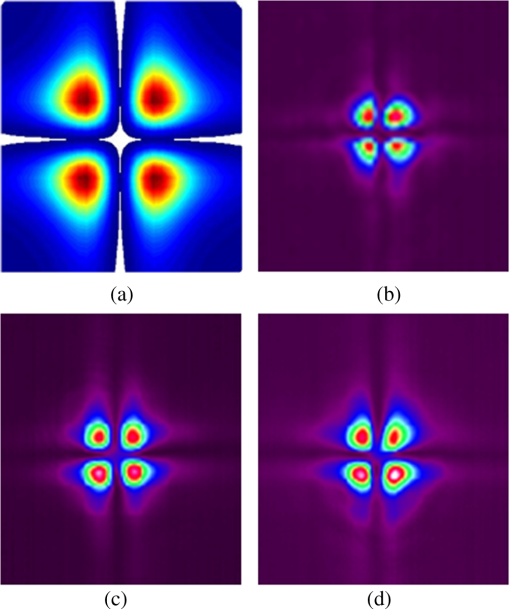 Three beams (3-mm in diameter at ) at wavelengths in the visible and the infrared regions were applied to study the wavelength dependence of diffraction and mode conversion using the HPM. As shown in Figs. 4(b)–4(d), for the three very different Bragg wavelengths (632.8, 975, and 1064 nm), the diffracted beam profiles exhibited the predicted four-lobed pattern. This clearly confirms our initial thesis that the binary phase profile is being preserved in the diffracted order for an extremely broad range of wavelengths. To further verify the binary phase step in the diffracted beam, an interferometric experiment was developed and is presented in Fig. 5(a). Fig. 5(a) Mach–Zehnder interferometer measuring the relative phase between the upper and lower lobes of the diffracted beam from the HPM. (b) The resulting interferogram with markers indicating two line cuts, and (c) the line cuts of the two lobes compared to each other, showing a relative phase difference. Note that the line cuts do not appear to be completely out of phase due to the slight tilt of the fringes, which can be seen in (b). 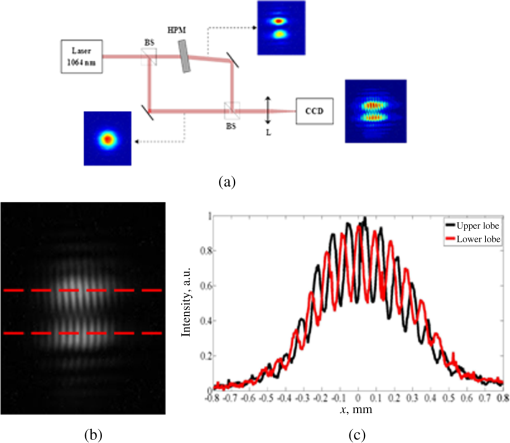 A 1064-nm laser was collimated and split into two arms of a Mach–Zehnder interferometer. The HPM was placed in one arm and rotated so that the beam incident on the HPM was at the Bragg angle, and the two beams were recombined and imaged onto a camera. In this experiment, the beam incident on the HPM was horizontally offset from the center so that the HPM acted as a two-sector binary mask. As shown in Figs. 5(b) and 5(c), the interference fringes of the upper and lower lobes produced by the HPM have a relative phase shift, confirming that the encoded phase profile is preserved in the diffracted beam at wavelengths far from the recording wavelength. 3.3.Fiber Mode ConversionIn this section, we consider another practical application for HPM elements by studying the conversion of fiber modes. This is of particular interest for applications such as power scaling of fiber lasers and amplifier systems, as higher-order modes (HOMs) propagating in fibers can carry more energy than the fundamental mode since their mode area is significantly larger. As a result, several fiber lasers and amplifier systems have been recently demonstrated with improved performances by using HOMs39–41 which, at some point, have to reconvert to the desired mode. In this context, we investigated the ability of the HPM to convert higher-order fiber modes into the fundamental mode; the usually preferred output beam of high-power fiber lasers and amplifiers. A diagram of the experiment is shown in Fig. 6, where a 1064-nm laser beam is coupled into a single-mode fiber to produce a high-quality fundamental mode Gaussian beam. The Gaussian beam is then collimated and directed onto a reflecting spatial light modulator (SLM). Applying the SLM encoding technique by Arrizón et al.,42 the incident beam was converted into the and HOMs. These modes were selected because their spatial phase pattern match the HPM with the encoded four-sector binary phase profile previously presented. The generated HOMs were then directed onto the HPM and the far-field of the diffracted order was analyzed. Fig. 6A 1064-nm beam passes through a single-mode fiber and then is diffracted from a spatial light modulator to generate various LP modes, which are then converted by a holographic phase mask mode converter and examined in the far-field. 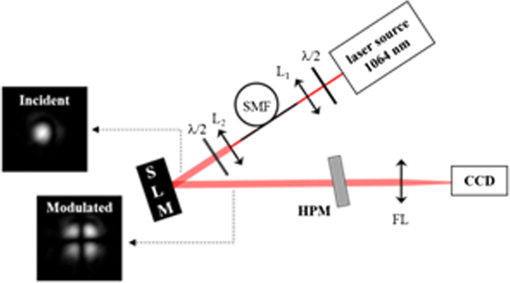 Because the LP modes form an orthonormal basis, we can define the conversion efficiency of a converted beam with respect to a desired mode by the overlap integral Here, is the electric field of the converted beam, is the desired LP mode, (*) represents the complex conjugation, and is the area. This integral will equal zero if the HPM does not alter the original mode and will equal unity for a complete conversion, and as such it may be considered as equivalent to the mode purity of the converted beam with respect to a given mode. Note that because the encoded phase profiles considered here are binary, they cannot convert a pure LP mode to another pure LP mode with 100% efficiency. Using Eq. (9), we find that the theoretical conversion efficiency from the fundamental mode to the mode (whether odd or even) using a binary phase mask is 71.8%, while the theoretical maximum conversion efficiency to the mode is 64.4%. The conversion efficiency from a pure HOM to the fundamental mode is identical to the conversion efficiency from the fundamental mode to the HOM.As shown in Fig. 7, by selecting different positions of the beam (indicated by the red spots) relative to the four-sectors of the HPM, various fiber modes can be generated. To calculate the experimental conversion efficiencies, we utilized an extension of Eq. (9), which is described in Ref. 20; the experimentally achieved conversion efficiencies are listed in Table 1. The fundamental mode has been converted to the even and odd modes as well as the mode with efficiencies up to 70%, indicating that the calculated maximum conversion efficiencies can be reached in the experiments. Slight deviations may be attributed to inhomogeneities in the sample and the finite extent of the transition region between areas with different phases. The reverse conversion efficiency from the mode to the fundamental mode is in excellent agreement with the calculated theoretical maximum, indicating that HPMs have the same conversion efficiencies as standard binary phase masks. Table 1Conversion efficiency of a binary holographic phase mask when converting between LP modes.
Fig. 7Far-field profiles of converted modes: (a) mode converted to higher order modes and (b) the mode converted to the mode. 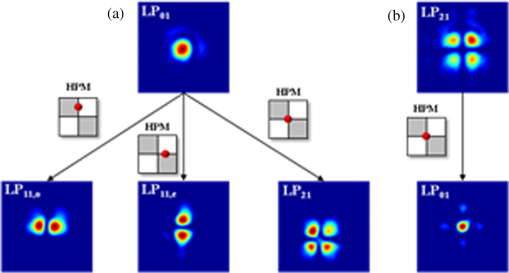 Note that, in addition to efficient mode conversion, size matching between the free space beam waist of the converted beam and the fiber mode also has to be considered for the overall mode converter efficiency. This issue has been addressed in detail for conventional narrow band phase plate mode converters.38 Similar overall efficiency results are expected for broadband HPM-based fiber mode converters, but are beyond the scope of this paper. 3.4.Simultaneous Mode Conversion and Beam CombiningBeam combining offers the potential to scale the power of laser systems beyond the limits of individual lasers. Currently, spectral beam combining and coherent beam combining are the two dominant methods in the effort to reach multikilowatt diffraction-limited beams. In parallel, as discussed above, fibers that support HOMs are considered to overcome the power limitations of fiber lasers and amplifiers. Therefore, the combination of several HOM beams from different lasers into one high-power fundamental mode beam suggests itself as a power scaling approach. Here, we describe a method to accomplish this task by taking advantage of the mode-converting capabilities of HPMs. While the ability of HPM elements to perform mode conversion is not unique,14,17 what is unique is the ability to simultaneously convert multiple beams into different modes while combining them into a single beam. As previously demonstrated, it is possible to angularly multiplex multiple HPMs or gratings into a single element. To perform beam combining, we utilize the same approach used in multiplexed volume gratings, where the periods and tilts of each grating are adjusted so that probe beams of different wavelengths and angles of incidence will diffract into the same channel.35–37 Here, we encode each grating with the appropriate phase profile so that each grating will also simultaneously perform mode conversion. To demonstrate this, we created two free-space converting/combining systems, illustrated in Fig. 8(a), where 1061 and 1064 nm beams are incident upon a multiplexed four-sector HPM at their respective Bragg angles. In the first combining/converting system, the original Gaussian beams were incident on the combining HPM without any additional phase elements added to the system, resulting in spectrally combined modes. The second system added two four-sector HPMs to each beam, converting each beam to the mode, and subsequently reconverting them to the fundamental mode while spectrally combining them. Fig. 8(a) A multiplexed four-sector HPM spectrally combines two beams at 1061 and 1064 nm. (b) If the initial four-sector HPMs are removed from the system, it combines two Gaussian beams while converting them to the mode. The (c) 1064-nm beam and (d) 1061-nm beam can also be separately converted. (e) If the initial four-sector HPMs are included in the system, then the Gaussian beams are converted to the mode and then reconverted back to a Gaussian beam. The reconverted beam profile closely matches the sum of the individual profiles at (f) 1064 nm and (g) 1061 nm. 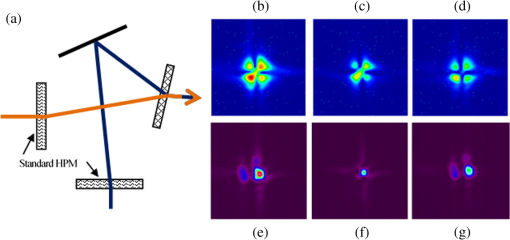 The far-field intensity profile of the combined beam in the first setup, shown in Fig. 8(b), shows good beam combination and conversion from the Gaussian mode. Note that the differences between the 1064 and 1061 nm far-field profiles in Figs. 8(c)–8(d) are due to different collimations between the beams rather than to a poor HPM conversion efficiency. The conversion from the mode to the fundamental mode in the second setup, shown in Fig. 8(e), is likewise demonstrated. While there are some wings remaining in the combined beam, this is predominately a limitation imposed by using HPMs as the initial converters, which creates increased alignment challenges, as seen in the individual beam profiles [Fig. 8(f)–8(g)]. Nevertheless, we have demonstrated that HPMs may be used for complex beam transformation-combination schemes. 4.ConclusionsWe have successfully demonstrated that binary phase profiles may be encoded into TBGs to form holographic phase masks HPMs, and that for any probe beam capable of satisfying the Bragg condition of the hologram the binary phase profile will be present in the diffracted beam. These holographic phase masks may be used to simultaneously diffract and convert both free space and fiber modes. They can also be multiplexed for beam combining in the same manner as homogenous multiplexed TBGs are used while converting the incident beams into a desired mode. This integration of beam combining and mode conversion at multiple wavelengths opens new optical design spaces in application areas such as high-power beam combining or mode multiplexing in optical communication systems. AcknowledgmentsWe would like to thank Prof. Boris Zeldovich for his fruitful discussions in developing the theoretical model for this work and OptiGrate Corp for supplying the PTR glass used in our experiments. This work was funded by ARO and HEL JTO through grants W911NF-10-1-0441 and W911NF-12-1-0450. ReferencesE. R. DowskiJr. and W. T. Cathey,
“Extended depth of field through wave-front coding,”
Appl. Opt., 34
(11), 1859
–1866
(1995). http://dx.doi.org/10.1364/AO.34.001859 APOPAI 0003-6935 Google Scholar
A. Greengard, Y. Y. Schechner and R. Piestun,
“Depth from diffracted rotation,”
Opt. Lett., 31
(2), 181
–183
(2006). http://dx.doi.org/10.1364/OL.31.000181 OPLEDP 0146-9592 Google Scholar
A. Castro, Y. Frauel and B. Javidi,
“Integral imaging with large depth of field using an asymmetric phase mask,”
Opt. Express, 15
(16), 10266
–10273
(2007). http://dx.doi.org/10.1364/OE.15.010266 OPEXFF 1094-4087 Google Scholar
N. Caron and Y. Sheng,
“Polynomial phase masks for extending the depth of field of a microscope,”
Appl. Opt., 47
(22), E39
–E43
(2008). http://dx.doi.org/10.1364/AO.47.000E39 APOPAI 0003-6935 Google Scholar
H. Zhao et al.,
“Cubic sinusoidal phase mask: another choice to extend the depth of field of incoherent imaging system,”
Opt. Laser Technol., 42 561
–569
(2010). http://dx.doi.org/10.1016/j.optlastec.2009.10.004 Google Scholar
B. Javidi and J. Horner,
“Optical pattern recognition for validation and security verification,”
Opt. Eng., 33
(6), 1752
–1756
(1994). http://dx.doi.org/10.1117/12.170736 Google Scholar
L. Neto and Y. Sheng,
“Optical implementation of image encryption using random phase encoding,”
Opt. Eng., 35
(9), 2459
–2463
(1996). http://dx.doi.org/10.1117/1.600848 Google Scholar
C. Cheng et al.,
“Optical joint transform encryption using binary phase difference key mask,”
Opt. Rev., 12
(5), 367
–371
(2005). http://dx.doi.org/10.1007/s10043-005-0367-5 PHRVAO 0031-899X Google Scholar
P. Kumar, J. Joseph and K. Singh,
“Impulse attack-free four random phase mask encryption based on a 4-f optical system,”
Appl. Opt., 48
(12), 2356
–2363
(2009). http://dx.doi.org/10.1364/AO.48.002356 APOPAI 0003-6935 Google Scholar
J. R. Leger, D. Chen and Z. Wang,
“Diffractive optical element for mode shaping of a Nd:YAG laser,”
Opt. Lett., 19
(2), 108
–110
(1994). http://dx.doi.org/10.1364/OL.19.000108 OPLEDP 0146-9592 Google Scholar
J. Yang and M. Wang,
“Analysis and optimization on single-zone binary flat-top beam shaper,”
Opt. Eng., 42
(11), 3106
–3113
(2003). http://dx.doi.org/10.1117/1.1615990 Google Scholar
X. Huang, M. Wang and C. Yu,
“High-efficiency flat-top beam shaper fabricated by a nonlithographic technique,”
Opt. Eng., 38
(2), 208
–213
(1999). http://dx.doi.org/10.1117/1.602255 Google Scholar
M. Wang, C. Yu and A. Varela,
“Efficient pseudo-nondiffracting beam shaping using a quasicontinuous-phase diffractive element,”
Opt. Eng., 40
(4), 517
–524
(2001). http://dx.doi.org/10.1117/1.1353800 Google Scholar
K. O. Hill et al.,
“Bragg gratings fabricated in monomode photosensitive optical fiber by UV exposure through a phase mask,”
Appl. Phys. Lett., 62 1035
–1037
(1993). http://dx.doi.org/10.1063/1.108786 APPLAB 0003-6951 Google Scholar
W. Mohammed et al.,
“Selective excitation of the mode in step index fiber using a phase mask,”
Opt. Eng., 45
(7), 074602
(2006). http://dx.doi.org/10.1117/1.2219425 Google Scholar
A. Shyouji et al.,
“Diffraction-grating-type phase converters for conversion of Hermite-Laguerre-Gaussian mode into Gaussian mode,”
Appl. Opt., 49
(9), 1513
–1517
(2010). http://dx.doi.org/10.1364/AO.49.001513 APOPAI 0003-6935 Google Scholar
M. Beresna et al.,
“Radially polarized optical vortex converter created by femtosecond laser nanostructuring of glass,”
Appl. Phys. Lett., 98 201101
(2011). http://dx.doi.org/10.1063/1.3590716 APPLAB 0003-6951 Google Scholar
C. Rotschild et al.,
“Adjustable spiral phase plate,”
Appl. Opt., 43
(12), 2397
–2399
(2004). http://dx.doi.org/10.1364/AO.43.002397 APOPAI 0003-6935 Google Scholar
K. Peithmann et al.,
“Low-spatial-frequency refractive-index changes in iron-doped lithium niobate crystals upon illumination with a focused continuous-wave laser beam,”
J. Opt. Soc. Am. B, 17
(4), 586
–592
(2000). http://dx.doi.org/10.1364/JOSAB.17.000586 JOBPDE 0740-3224 Google Scholar
M. SeGall et al.,
“Binary volume phase masks in photo-thermo-refractive glass,”
Opt. Lett., 37
(7), 1190
–1192
(2012). http://dx.doi.org/10.1364/OL.37.001190 OPLEDP 0146-9592 Google Scholar
M. Bass, Handbook of Optics, 2nd ed.McGraw-Hill, New York, NY
(1994). Google Scholar
D. Mawet et al.,
“Achromatic four quadrant phase mask coronagraph using the dispersion of form birefringence,”
Astronomy with High Contrast Imaging, Cambridge University, Cambridge
(2003). Google Scholar
J. Rosen, M. Segev and A. Yariv,
“Wavelength-multiplexed computer-generated volume holography,”
Opt. Lett., 18
(9), 744
–746
(1993). http://dx.doi.org/10.1364/OL.18.000744 OPLEDP 0146-9592 Google Scholar
G. A. Rakuljic, V. Leyva and A. Yariv,
“Optical data storage by using orthogonal wavelength-multiplexed volume holograms,”
Opt. Lett., 17
(20), 1471
–1473
(1992). http://dx.doi.org/10.1364/OL.17.001471 OPLEDP 0146-9592 Google Scholar
T. D. Gerke and R. Piestun,
“Aperiodic volume optics,”
Nat. Photonics, 4 188
–193
(2010). http://dx.doi.org/10.1038/nphoton.2009.290 NPAHBY 1749-4885 Google Scholar
H. Kogelnik,
“Coupled wave theory for thick volume holograms,”
Bell System Tech. J., 45
(9), 2909
–2944
(1969). http://dx.doi.org/10.1002/j.1538-7305.1969.tb01198.x BSTJAN 0005-8580 Google Scholar
I. Ciapurin, L. Glebov and V. Smirnov,
“Spectral combining of high-power fiber laser beams using Bragg grating in PTR glass,”
Proc. SPIE, 5335 116
–124
(2004). http://dx.doi.org/10.1117/12.533740 PSISDG 0277-786X Google Scholar
K. Aoki et al.,
“Selective multimode excitation using volume holographic mode multiplexer,”
Opt. Lett., 38
(5), 769
–771
(2013). http://dx.doi.org/10.1364/OL.38.000769 OPLEDP 0146-9592 Google Scholar
Y. Wakayama et al.,
“Mode demultiplexer using angularly multiplexed volume holograms,”
Opt. Express, 21
(10), 12920
–12933
(2013). http://dx.doi.org/10.1364/OE.21.012920 OPEXFF 1094-4087 Google Scholar
S. Wu et al.,
“Broadband angular filtering with a volume Bragg grating and a surface grating pair,”
Opt. Lett., 39
(14), 4068
–4071
(2014). http://dx.doi.org/10.1364/OL.39.004068 OPLEDP 0146-9592 Google Scholar
J. Lumeau et al.,
“Origin of crystallization-induced refractive index changes in photo-thermo-refractive glass,”
Opt. Mater., 32 139
–146
(2009). http://dx.doi.org/10.1016/j.optmat.2009.07.007 Google Scholar
L. B. Glebov,
“Photochromic and photo-thermo-refractive glasses,”
Encyclopedia of Smart Materials, 2 John Wiley & Sons, Hoboken, New Jersey
(2002). Google Scholar
I. Divliansky et al.,
“High-power semiconductor lasers for applications requiring GHz linewidth source,”
Proc. SPIE, 7198 71981N
(2009). http://dx.doi.org/10.1117/12.810058 PSISDG 0277-786X Google Scholar
G. Chang et al.,
“Femtosecond Yb-fiber chirped-pulse-amplification system based on chirped-volume Bragg gratings,”
Opt. Lett., 34
(19), 2952
–2954
(2009). http://dx.doi.org/10.1364/OL.34.002952 OPLEDP 0146-9592 Google Scholar
D. Ott et al.,
“Scaling the spectral beam combining channels in a multiplexed volume Bragg grating,”
Opt. Express, 21
(24), 29620
(2013). http://dx.doi.org/10.1364/OE.21.029620 OPEXFF 1094-4087 Google Scholar
C. Lu et al.,
“Coherent beam combination of fiber laser arrays via multiplexed volume Bragg gratings,”
in Conf. on Lasers and Electro-Optics: Science and Innovations,
(2012). Google Scholar
A. Jain et al.,
“Efficient coherent beam combining of fiber lasers using multiplexed volume Bragg gratings,”
in Conf. on Lasers and Electro-Optics: Science and Innovations,
(2012). Google Scholar
K. Igarashi et al.,
“Performance evaluation of selective mode conversion based on phase plates for a 10-mode fiber,”
Opt. Express, 22
(17), 20881
–20893
(2014). http://dx.doi.org/10.1364/OE.22.020881 OPEXFF 1094-4087 Google Scholar
J. W. Nicholson et al.,
“A higher-order-mode Erbium-doped-fiber amplifier,”
Opt. Express, 18
(17), 17651
–17657
(2010). http://dx.doi.org/10.1364/OE.18.017651 OPEXFF 1094-4087 Google Scholar
J. W. Nicholson et al.,
“Scaling the effective area of higher-order-mode erbium-doped-fiber amplifiers,”
Opt. Express, 20
(22), 24575
–24584
(2012). http://dx.doi.org/10.1364/OE.20.024575 OPEXFF 1094-4087 Google Scholar
X. Peng et al.,
“High-order mode fiber enables high energy chirped-pulse amplification,”
Opt. Express, 21
(26), 32411
–32416
(2013). http://dx.doi.org/10.1364/OE.21.032411 OPEXFF 1094-4087 Google Scholar
V. Arrizón et al.,
“Pixelated phase computer holograms for the accurate encoding of scalar complex fields,”
J. Opt. Soc. Am. A, 24
(11), 3500
–3507
(2007). http://dx.doi.org/10.1364/JOSAA.24.003500 JOAOD6 0740-3232 Google Scholar
BiographyMarc SeGall received his PhD in optics from the University of Central Florida in Orlando, Florida, USA, in 2013. He is currently a research scientist at Physical Optics Corporation. Prior to joining Physical Optics, he was a graduate student at the University of Central Florida where he researched the effects of volume phase masks. His current research interests include head worn displays, non-mechanical beam steering systems, and holography. Ivan Divliansky received his PhD in electrical engineering/materials science from The Pennsylvania State University in State College, Pennsylvania, USA in 2004. Since 2007, he has been a senior research scientist at CREOL, the College of Optics and Photonics at the University of Central Florida in Orlando. His current research interests include high-power laser beam combining, diode and fiber lasers systems design, implementation of volume Bragg gratings in different photonics areas, vector beams generation, and others. Clémence Jollivet received her PhD in optics from the University of Central Florida in 2014. Highlights of her work are compiled in the PhD dissertation entitled “Specialty fiber lasers and novel fiber devices.” Currently, her research interests include design and fabrication of specialty optical fibers, specialty fiber lasers, novel fiber devices, and advanced characterization techniques such as modal analysis. Since 2014, she has been working as a scientist in the Fiber R&D Department of Nufern Inc. Axel Schülzgen received his PhD in physics from Humboldt-University of Berlin, Germany, in 1992. Since 2009, he has been a professor of optics at CREOL, the College of Optics and Photonics, University of Central Florida in Orlando. Prior to joining CREOL, he was a faculty member at the College of Optical Sciences, University of Arizona in Tucson. His current research interests include optical fiber devices and components with applications in fiber laser systems and fiber optic sensing. |
||||||||||||||||||