2.1.

Two-Photon Fabrication and Collection of Microtools

The microtools consist of a free-floating waveguide attached to four spherical handles. The design of the microtools, as shown in Fig. 1(a), is chosen so that it can obtain 6 degrees of freedom while being optically manipulated. The input facet of a microtool is placed at the geometric center of the handles for easy tracking but also to keep the trapping beams a safe distance away from its coupling beam. The structures are fabricated using a 2PP-based commercial setup (Nanoscribe Photonic Professional, $\lambda =780\mathrm{nm}$, 100 fs pulse duration, 800 MHz repetition rate, $>140\mathrm{mW}$ average power) with associated photoresist (IPL-780, $n=1.50$ after exposure). The structures are fabricated on top of a glass cover slip. The writing parameters for 2PP fabrication are set to 60% laser power and $50\mu \mathrm{m}/\mathrm{s}$ scanning speed.

Fig. 1

(a) Microtools, coined as wave-guided optical waveguides, are fabricated using two-photon photopolymerization. (b) Collection of microtools from the glass substrate for subsequent trapping and coupling experiments.

The common and simplest way to design structures to be fabricated using 2PP is to use a 3-D rendering software and extract the volumetric data. A lateral slicing of this volume is then performed and the fabrication is carried-out by scanning line by line from the bottom and proceeding upward using the extracted Cartesian coordinate points. This approach is suitable for structures such as woodpiles, but for structures such as our microtools where there are hanging parts, this will be inherently problematic during fabrication. Another concern is the presence of stair-like artifacts from the slicing. We do not want this in the waveguide part of our microtools as this may cause less optimized coupling. Since the 2PP fabrication setup requires 3-D coordinates for the scanning trajectory, we define each microtool as a composite structure of basic volumetric shapes (e.g., spheres, toroid) described by parametric equations to ensure a continuous and smooth writing process. For example, the trapping handles are defined using the parametric equation of a sphere with a radius of $4\mu \mathrm{m}$. The bent part of the waveguide is defined using a quarter of a toroid with bending radius of $6\mu \mathrm{m}$, and the core diameter of the waveguide is $1\mu \mathrm{m}$ with a tapered tip. The trapping medium (water with $n=1.33$) serves as the “cladding” for the waveguide part. Given the index of refraction of the polymerized microtool and the water-based “cladding,” we have calculated the effective NA to be 0.69. Using a 532 nm laser for generating the coupling beams and the aforementioned structural parameters of the microtools, we have calculated the normalized waveguide parameter to be $V=4.075$, which suggest a multimode output. We have not, however, performed a rigorous mode analysis as this is outside the scope of this work. The presence of a small bending radius and tapering tip would potentially further complicate this analysis. Rigorous treatment for such cases is found in the literature.^13,14

To perform trapping and coupling experiments, a few microtools were transferred from the glass substrate to a cytometry cell. This was done by carefully picking up the microtools using a small capillary tube attached to a microliter syringe and subsequently transferring it to a cuvette, as shown in Fig. 1(b).

2.2.

Object-Tracking and Hologram Calculation

The microtools are manipulated using the spherical handles held by the counter-propagating trapping beams (${\lambda }_{\mathrm{trap}}=1070\mathrm{nm}$). In this scenario, a lateral movement of a single microtool can be accomplished by simply dragging the beams along the lateral direction. The axial movement can be performed by changing the intensity ratio of the trapping beams. As the microtool moves in 3-D space, we require its coupling beam (${\lambda }_{\mathrm{coup}}=532\mathrm{nm}$) to track and follow it for continuous addressing. The lateral displacements $\mathrm{\Delta }{x}^{\prime }$ and $\mathrm{\Delta }{y}^{\prime }$ of each microtool can be readily obtained from the trapping interface since the trapping beams uses an imaging geometry, and thus only a simple scaling is needed for the hologram calculations. The axial coordinate cannot be inferred directly due to the counter-propagating nature of the trapping beams. Hence, we need to use an object tracking routine on the side-view imaging to automatically get the axial displacement parameter $\mathrm{\Delta }{z}^{\prime }$. The built-in tracking routine in LabVIEW uses the mean shift algorithm. It is a nonparametric iterative algorithm used in pattern recognition and computer vision.^15,16 The algorithm is able to determine the position of the microtool at a video frame rate. The procedure is summarized in Fig. 2(a).

Fig. 2

(a) Schematic diagram of the biophotonics workstation for trapping and coupling experiments. (b) Graphical demonstration of diffractive coupling to a single microtool. The microtool is moved in three-dimensional (3-D) space using the counter-propagating trapping beams holding its spherical handles. The diffractive phase holograms are used to modulate each coupling beam to dynamically follow the position of the respective microtool in real time.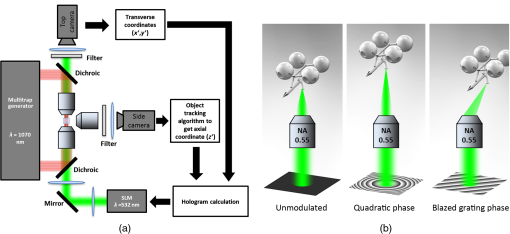

The required phase holograms for the lateral and axial movements of each coupling beam are calculated using the simplified “blazed grating and quadratic phases” approach, and are given by

2.3.

Experimental Setup with a Generalized Phase Contrast Light Shaper

The biophotonics workstation uses a counter-propagating beam-trapping geometry. The top and bottom trapping beams are relayed into the sample by two long working distance and low-NA objectives (Olympus LMPL $50\times$ IR objectives, $\mathrm{WD}=6\mathrm{mm}$, and $\mathrm{NA}=0.55$). A side-view imaging objective lens (Mitutuyo MPlanApo $20\times$, $\mathrm{WD}=20\mathrm{mm}$, and $\mathrm{NA}=0.42$) is added for more intuitive 3-D trapping and for capturing the emerging output beam from the tip of each microtool. The setup is described in Fig. 2(a). A fluorescence dye (Rhodamin 6G) is added to the trapping medium to aid in visualizing the coupling beams using the side-view imaging.

The holographic setup uses a single focusing geometry where the phase patterns are projected to an LCoS SLM (Hamamatsu Photonics, $792\times 600\text{pixels}$, $9.9\mathrm{mm}\times 7.5\mathrm{mm}$ active area). To increase the efficiency of the coupling beams, a preliminary beam shaping using the GPC method¹⁸ is performed to match the cross section of the SLM addressing window. A compact module containing the main components of the GPC is added to the holographic setup as shown in Fig. 3. We refer to this module as the so-called GPC light shaper (LS). The sizes of the phase mask and phase contrast filter are optimized according to the values in the literature.¹⁹ The use of the GPC LS allows efficient photon management compared to the more common practice of hard-truncation^20,21 and can work with a broad range of wavelengths.²²

Fig. 3

Schematic diagram of the holographic coupling light setup. The GPC light shaper (LS) is placed before the spatial light modulator (SLM) to perform preliminary beam shaping to match the shape of the SLM. Unlike hard-truncation where a significant portion of light is discarded, the GPC LS only redirects photons to the active SLM window.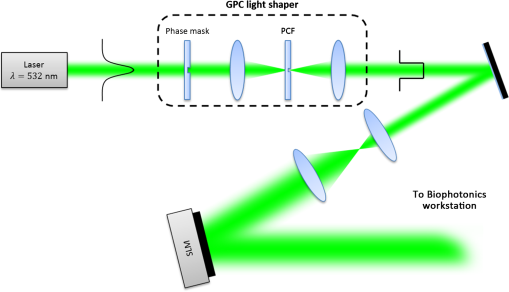

The GPC LS works by introducing a phase shift to the incident Gaussian beam using a phase mask that has a phase shifting region corresponding to the shape of the SLM. A lens takes the optical Fourier transform of the phase shifted field in the plane of the phase contrast filter which creates a synthetic reference wave from the low spatial frequencies. A second lens takes another optical Fourier transform of the field and the resulting pattern at the output plane is a speckle-free intensity distribution corresponding to the layout of the input phase mask. Unlike the common method of hard-truncation where photons are discarded, the GPC LS redirects photons to where they are needed. The holographic setup with the integrated GPC LS is shown in Fig. 3.

3.1.

Image Segmentation

A long-pass filter with a cutoff wavelength at 550 nm is placed before the applied CMOS camera to remove the coupling beams and use the fluorescence signal to measure the total power output at the tip of the microtool. We use an image segmentation approach based on the color channel of the captured images to ensure that we compute only the fluorescence signal. We take advantage of the RGB color model used to represent the captured images. The RGB color model is an additive model where different colors are produced by mixing the three primaries (i.e., red, green, and blue).²³ A cyan filter is installed with the white LED for the side illumination. The resulting cyan color illumination registers in the CMOS camera as having an RGB value of (0, 255, 255) and the microtools are practically transparent. Thus, the greenish fluorescence signal will result in localized variations in the red channel only. Figure 4 shows a particularly good localization of the fluorescence signal at the tip of the microtool. Furthermore, we can calculate the “center of mass” from the red channel data to pinpoint the location of the tip and integrate the total power within the vicinity. This procedure is similar to tracking fluorescent low density lipoprotein receptor molecules.²⁴

Fig. 4

Image segmentation based on the RGB channels in a true-color image. The red channel shows a particularly good localization of the fluorescence signal.

3.2.

Brownian Motion of the Trapped Microstructure

A crucial step for optimal coupling is to account for the uncontrolled movement of the trapped microstructures due to Brownian motions. We measure the amount of fluctuations of each microtool by trapping it in a fixed position and use the output coupling beam at the tip as a light beacon to locate its position. The trajectories for both GPC-enhanced and non-GPC coupling beams are plotted in Figs. 5(a) and 5(b), respectively.

Fig. 5

Brownian motion trajectories for (a) GPC-enhanced and (b) a non-GPC coupled microtool. (c) Power variations at the output are observed. The dashed lines represent the average power for both coupling cases.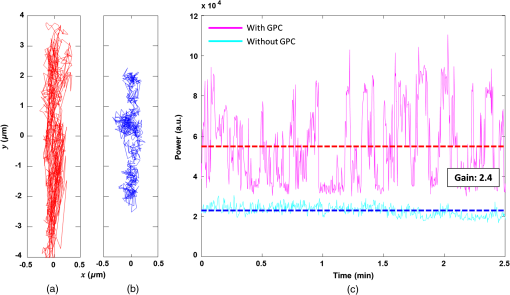

In both coupling cases, there is a small movement along the lateral direction, but a large variance along the axial direction. This is due to the relatively weak axial confinement obtained by low-NA counter-propagating beam traps. However, there are more pronounced fluctuations in the GPC-enhanced coupled microtool. We attribute this to the stronger recoil of the structure from the more intense coupling beam.²⁵ This effect can be minimized by modifying the shape of the handles.^5,26 Figure 5(c) shows the output power fluctuations for the duration of our observation. We took the average power for both coupling cases and took the ratio to calculate the gain. We found the value to be 2.4 for a GPC-enhanced coupled microtool.

3.3.

Coupling Through Optically Manipulated Microstructure

Coupling has been tested for both lateral and axial displacements of the microtools, separately. The lateral movement is performed by dragging its associated trap using a computer interface. The coordinate variables are then grabbed to calculate the required grating phase. For axial coupling, the position of a microtool is obtained from the built-in object tracking routine in LabVIEW. The obtained axial displacement is then used to calculate the required quadratic (lens) phase. The results for the lateral and axial coupling are shown in Figs. 6 and 7, respectively. The total power for each case is calculated frame by frame for the duration of the observations ($\sim 6\mathrm{s}$) and the average power for each coupling case is taken to compute the gain.

Fig. 6

(a) Power variations as a microtool are moved laterally. The dashed lines represent the average power value. (b) Selected frames are stacked together to form a trace of the trajectory of the microtool while it is being optically manipulated. (Video 1, QuickTime, 4.66 Mb.) [URL: http://dx.doi.org/10.1117/1.OE.54.11.111308.1].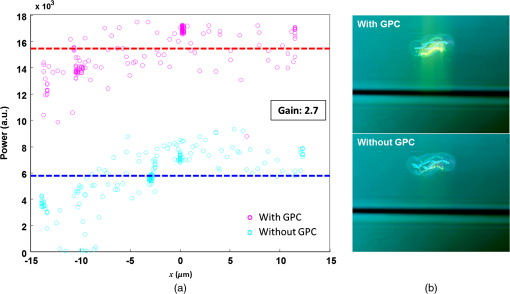

Fig. 7

(a) Power variations as a microtool are moved axially. The dashed lines represent the average power value. (b) Selected frames are stacked together to form a trace of the trajectory of the microtool while it is being optically manipulated. (Video 2, QuickTime, 4.49 Mb.) [URL: http://dx.doi.org/10.1117/1.OE.54.11.111308.2].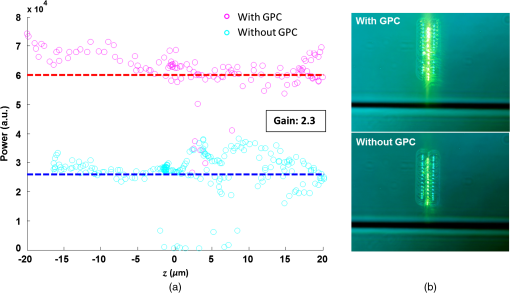

In both lateral and axial coupling experiments, the GPC-enhanced coupled microtools show the highest total output power. This boost in output tip-light from the microtools can have potential applications when the aim is to trigger nonlinear light phenomena in biological samples. The microtools can be coated with gold nanoparticles to trigger local field enhancement for a better fluorescence signal.²⁷ In Fig. 8, we demonstrate coupling following an arbitrary path.

Fig. 8

Trapping and coupling of a microtool tracing out an arbitrary path. Selected frames are stacked together to form a trace of the path. (Video 3, QuickTime, 584 Kb.) [URL: http://dx.doi.org/10.1117/1.OE.54.11.111308.3].