|
|
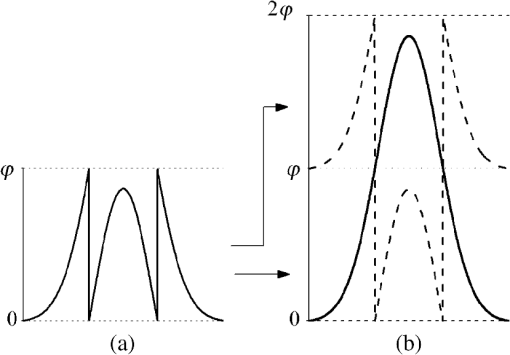
1.IntroductionPhase extraction methods are used in different coherent signal processing areas, such as optical and microwave interferometry,1 magnetic resonance imaging,2 synthetic aperture radar,3 and Fourier transform optical coherent tomography,4 among others. In these areas, the signal modulates a harmonic function and phase extraction algorithms are used to recover the signal. The recovered signal within the principal branch of the harmonic function exhibits a series of discontinuities, which need to be removed to obtain the real signal. This process, known as phase unwrapping, is the final phase extraction step. We collect these discontinuities in a wrapping map, normally overlooked based on the principle that the proposed methods aim to recover the real phase map knowing its expected continuity properties. Since phase unwrapping was first showed in optical interferometry phase extraction,5,6 there have been extensive studies to recover the correct phase map. Because of the presence of noise, signal discontinuities, and undersampling, phase unwrapping is considered to be one of the most difficult problems in mathematics and engineering.7 To date, there are two main approaches to the phase unwrapping problem, which can be classified in path following methods of minimum-norm methods.8–10 Independent of the approach, a definite solution for phase unwrapping remains an open problem. On this note, an alternative solution to the phase unwrapping problem focusing on the properties of the phase wrapping map instead of the real phase signal properties is presented. 2.Phase UnfoldingPhase extraction methods retrieve a wrapped phase from a harmonic function confined in the main branch of the function, which is normally a band in either [) or [). Because phase is a relative quantity, we can focus only on the [) band without loss of generality. In order to obtain an insight on the phase unwrapping problem instead of looking at the problem as the final step in a phase extraction methods as is customary, let us look at the problem from the solution point of view. In other words, starting from the correct phase map [Fig. 1(a)], the wrapped phase is obtained [Fig. 1(b)] by adding multiples of [Fig. 1(c)] to contain in the [) band. The form of the integer-valued correcting field [Fig. 1(c)], or phase wrapping map , is dependent on the properties of . Fig. 1For a amplitude Gaussian curve (a) genuine unwrapped phase , (b) corresponding wrapped phase within [) values, and (c) integer-valued multiple correcting field, or phase wrapping map . 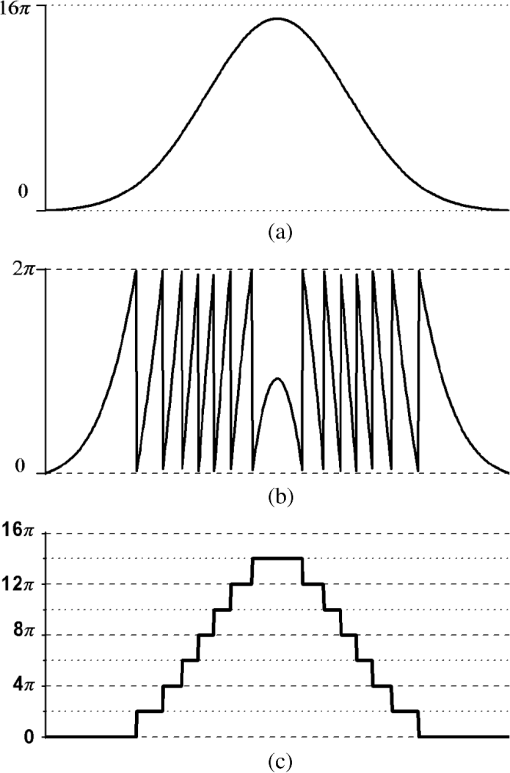 The aim of the phase unwrapping methods aforementioned is to add a correct multiple of to the wrapped phase such that a continuous unwrapped phase map is reconstructed. These methods focus on the properties of the expected phase map and the challenge is to restore a function free of the jumps. As mentioned, instead of focusing in the properties of , here we investigate the properties of the phase wrapping map . To be more precise, focus on an alternative construction of . To do such and bearing in mind that if the phase map is sampled with scaled harmonic functions with a multiple of periodicity, in principle, we can obtain the correct solution after an adequate phase unwrapping procedure. Considering using powers of two multiples of () is of particular interest. By using this approach, an insight on the phase wrapping map is obtained and it is found that it can be properly decomposed by simpler phase wrapping maps. The first task is to obtain the minimum power of two multiples of , which contains . This is, look for , which is the minimum integer such that After determining this number, consider wrapping planes in subpowers of two multiples of , , (Fig. 2) in such a way that iterative wrapping maps , [Figs. 3(b), 3(d), 3(f), and 3(h)] are obtained by wrapping the immediate previous wrapped function () by the next subpower of two multiples of . By doing so the ’th wrapping map has binary values: zero or . Notice that by construction, the position, but not necessarily the sign, of the phase jumps for each wrapping map is contained in the next one. Thus, the following intermediate wrapped functions are constructed [Figs. 3(a), 3(c), 3(e), and 3(g)]: Fig. 2Alternative wrapping planes separated in a sequence for the function on Fig. 1. In this case, and planes for , and are considered. 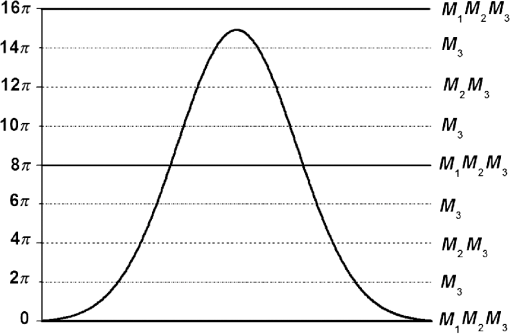 Fig. 3Intermediate wrapped functions and intermediate wrapped maps for the example in Fig. 1: (a) , (b) used to fold , (c) , (d) used to fold , (e) , (f) used to fold , (g) ; this is the final wrapped phase within [) values, and (h) used as constructing wrapped function in the phase unfolding algorithm. 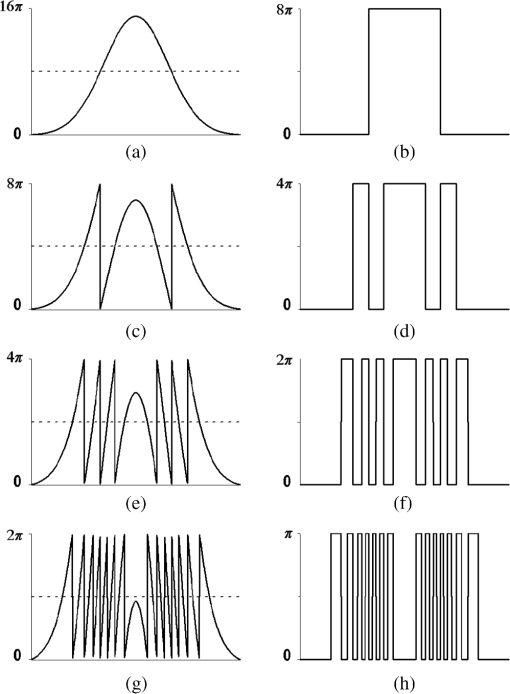 The wrapping map down to the main branch () is therefore the sum of the binary intermediate wrapping maps. Using this approach instead of finding the correct multiple of for phase unwrapping, the solution is reduced to reconstruct each step backward. In other words, instead of unwrapping the phase, we iteratively unfold the phase. where . Unfolding the phase consists on finding and removing iteratively . The benefit is that the partial wrapping map consists of only zeroes and ones.In spite of the apparent advantage using this binary approach, the unfolding problem is as complex as the unwrapping approach. This complexity is made evident by manipulating an intermediate wrapped function placed on top of itself, thus mimicking one unfolding step. Using this construction, it is found that each point has two possible solutions (Fig. 4): Equation (6) is the correct solution [Fig. 4(b) solid line], whereas Eq. (7) is a false solution, which increases the amount of wrapping [Fig. 4(b) dotted line]. Nevertheless, the correct solution is found among only two possible solutions and phase unwrapping has been reduced to find the correct one among these two.3.Path-Following Phase Unfolding AlgorithmDifferent approaches for unfolding the phase have been explored. Here, a straightforward path following method is presented. In order to implement the basic path following phase unfolding process, notice that if the intermediate phase wrapped function is shifted by , the following folding step produces the same wrapped function . This property is used to simplify the unfolding process. Thus, the path following phase unfolding process can be performed by splitting the task down into the following steps:
Fig. 5(a) Intermediate wrapped function , the arrows show the required displacements to roll the phase by , as described in the text, (b) complementary intermediate wrapped function after a roll, and (c) difference between and signifying . 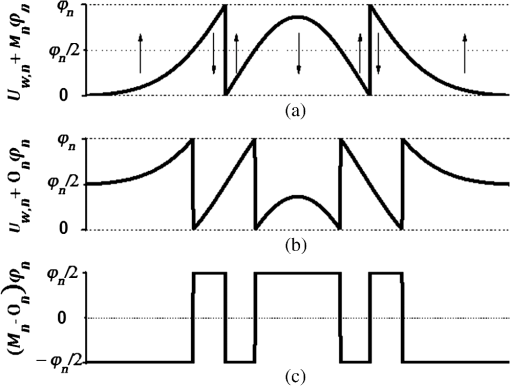 Using this procedure after iterations, in which the final value of is , the correct phase map is recovered. The algorithm performs the unfolding procedure by locating phase jumps on a binary function governed by Eq. (8). Therefore, in contrast to regular phase unwrapping techniques instead of searching for discontinuities on a stepwise continuous function at each point to execute the unwrapping decision like ice walking the unfolding decision is made only on abrupt changes in in a cliff hopping manner. Phase unfolding produces times more operations than phase unwrapping methods but has the advantage that the number of discontinuity correcting decisions is reduced to the phase jumps clearly identified on [Eq. (8)], which decrease on each iteration. Phase unfolding also has the same restrictions than conventional phase unwrapping: is limited by signal noise, under sampling beyond Shannon–Nyquist limit and discontinuities in the wrapped signal. Furthermore, the first iteration in the unfolding algorithm requires an additional downfolding the wrapped phase to half of the main branch [Fig. 3(h)], thus increasing the sampling limitations to fulfill the Shannon–Nyquist limit. On the other hand, errors due to false wrapping do not propagate as it does in the path following phase unwrapping because of the local phase jump detection in Eq. (7). As an example of the phase unfolding algorithm, a unitary circle function closely related to third order spherical aberration with amplitude is analyzed (Fig. 6). Figure 6(a) shows the expected result of a phase extraction method confined in the [) band. In this case, is 4 (), therefore unfolding phase unwrapping is achieved in three steps as shown. On each consecutive step [Figs. 6(b)–6(d)], the phase unfolds as a folding cup opening until the correct phase map is recovered in Fig. 6(d). Fig. 6Phase unfolding algorithm operating on the unitary circle function {}. Only half of the function is shown to better appreciate the effect of the phase unfolding algorithm. (a) Original wrapped function in the [) domain, (b) first unfolding iteration in the [) domain, (c) second iteration in the [) domain, and (d) third and final iteration recovering the correct phase map with a amplitude. 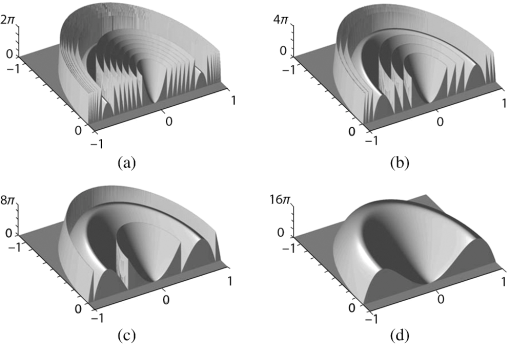 For the simple path following the method demonstrated, phase unfolding presents some advantages with respect to phase unwrapping, namely the correct identification of phase jumps, a decrease number of discontinuity correcting decisions and splitting the problem to binary maps [Eq. (5)]. It also presents disadvantages such as tighter limitation in the sampling period and the number of computational steps. Both approaches are similarly sensitive to signal noise or discontinuities in the signal. Comparable computational time has been observed using either approach. Further research is required to incorporate simultaneously the properties of both the real phase map and the phase wrapping map in phase unwrapping or unfolding algorithms. Additional studies also need to be conducted to fully determine the effect of the wrapping map decomposition [Eqs. (4) and (5)] on either path following or minimum norm unwrapping methods. 4.ConclusionsIn conclusion, an alternative method for phase unwrapping, named phase unfolding, has been presented by exploring the properties of the phase wrapping map decomposed in a series of binary intermediate wrapping maps. An effective iterative algorithm for path following phase unfolding was also presented, identifying some advantages and disadvantages with respect to standard phase unwrapping. AcknowledgmentsThe author would like to thank Dr. Blas M. Rodriguez-Lara for fruitful discussions. This work was partially funded by grant CONACyT CB-2011-01-168558. ReferencesM. A. Schofield and Y. Zhu,
“Fast phase unwrapping algorithm for interferometric applications,”
Opt. Lett., 28
(14), 1194
–1196
(2003). http://dx.doi.org/10.1364/OL.28.001194 OPLEDP 0146-9592 Google Scholar
L. Ying,
“Phase unwrapping,”
Wiley Encyclopedia of Biomedical Engineering, John Wiley & Sons, Hoboken, New Jersey
(2006). Google Scholar
B. Osmanoglu et al.,
“On the importance of path for phase unwrapping in synthetic aperture radar interferometry,”
Appl. Opt., 50
(19), 3205
–3220
(2011). http://dx.doi.org/10.1364/AO.50.003205 APOPAI 0003-6935 Google Scholar
N. A. Nassif et al.,
“In vivo high-resolution video-rate spectral-domain optical coherence tomography of the human retina and optic nerve,”
Opt. Express, 12
(3), 367
–376
(2004). http://dx.doi.org/10.1364/OPEX.12.000367 OPEXFF 1094-4087 Google Scholar
M. Takeda, H. Ina and S. Kobayashi,
“Fourier-transform method of fringe-pattern analysis for computer-based topography and interferometry,”
J. Opt. Soc. Am., 72
(1), 156
–160
(1982). http://dx.doi.org/10.1364/JOSA.72.000156 JOSAAH 0030-3941 Google Scholar
K. Itoh,
“Analysis of the phase unwrapping algorithm,”
Appl. Opt., 21
(14), 2470
–2470
(1982). http://dx.doi.org/10.1364/AO.21.002470 APOPAI 0003-6935 Google Scholar
D. Ghiglia and M. Pritt, Two-Dimensional Phase Unwrapping Theory, Algorithms and Software, John Wiley & Sons, Hoboken, New Jersey
(1998). Google Scholar
V. V. Volkov and Y. Zhu,
“Deterministic phase unwrapping in the presence of noise,”
Opt. Lett., 28
(22), 2156
–2158
(2003). http://dx.doi.org/10.1364/OL.28.002156 OPLEDP 0146-9592 Google Scholar
M. Servin et al.,
“Phase unwrapping with a regularized phase-tracking system,”
Appl. Opt., 37
(10), 1917
–1923
(1998). http://dx.doi.org/10.1364/AO.37.001917 APOPAI 0003-6935 Google Scholar
H. Y. H. Huang et.al.,
“Path-independent phase unwrapping using phase gradient and total-variation (TV) denoising,”
Opt. Express, 20
(13), 14075
–14089
(2012). http://dx.doi.org/10.1364/OE.20.014075 OPEXFF 1094-4087 Google Scholar
|