|
|
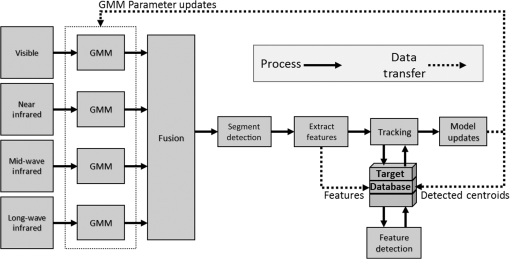
1.IntroductionAutomatic detection and tracking of moving targets in full motion video from aerial imaging systems such as unmanned aerial vehicles (UAV) and satellites are of significant interest in the defense and security communities.1–3 These aerial platforms can remain undetected from prospective targets and encompass a large surveillance area. Satellites have been a primary “spy” tool for decades and continue to provide for their respective nations, but their coverage is limited by orbital mechanics, and is hence not always sufficiently timely, nor can a satellite generally be launched on demand to address a short-term tactical matter in the field. Vast amounts of research have been invested in UAV surveillance, and UAVs have been a significant resource for intelligence gathering.1,4,5 Large areas, such as open waters or borders, can be surveyed for intrusions, regions can be assessed for building of weapon facilities, or urban areas can be checked for potential threats. The urban environment is of interest for this work. Urban environments provide significant challenges to the problem of automatically detecting and tracking moving vehicles. These areas generally contain complicated clutter and a collection of different targets, e.g., humans, buildings, roads, and vehicles. Each of these different entities also varies greatly in shape and size that challenge automatic target detection and recognition algorithms. Trees, buildings, tunnels, and other formations result in object occlusions that affect the appearance of the targets and sometimes completely block the targets from view for a few to several consecutive frames. Images in the visible spectrum (0.4 to ) provide reflected spectral information that creates contrast between targets, and between targets and the background. The visible spectrum requires good illumination during the daytime hours. Imaging in the long-wave infrared (LWIR) band (8 to ) is dependent on the temperature and thermal emissivity of the target, but is not dependent on solar illumination, and thus provides nighttime imaging capabilities. The effects of atmospheric aerosols also play a role in these imaging modalities. For example, Mie scattering significantly hinders the performance of visible imaging in the presence of fog aerosols.6 The wavelengths of the midwave infrared (MWIR) and LWIR bands are longer than the visible wavelength, making them less susceptible to the attenuation due to Mie scattering, and thus provide some immunity to the effects of fog and other aerosols on image quality.6 The approach of multispectral detection and tracking fuses information obtained from images in different spectral bands to improve detection statistics. Various approaches have been taken in algorithm development for detecting and tracking using multispectral imagery where the fusion framework takes place in three stages of the processing: pixel level,7–11 feature level,12–14 and decision level.15 Fusion at the pixel level creates a single image that is a composition of the pixels in the multispectral images. It is often used to create a single image that is interpreted by an operator.16,17 The combination of pixels into a single image is difficult as there is not always a correlation of the pixel values from the different spectral images, and it has been found that a mild anticorrelation exists between the visible and LWIR bands.18 Feature-level fusion combines the by-product of processing of individual spectral bands. These processing products include numerous classifications of features, such as foreground maps, histograms, edge contours, and texture features. Processing of individual spectral bands allows feature extraction algorithms to be optimized for each band. In decision-level fusion, processing is performed on each independent spectral band where a decision is made, such as object size and location. These decisions are fused based on band-specific confidence levels to give an overall decision. To exploit benefits of each spectral band, feature-level and decision-level fusion allow algorithm development tailored for their respective bands. Algorithms fusing background models from different image modalities to create a common foreground for target detection have been demonstrated.12–15 Chen and Wolf13 model the foreground in both visible and LWIR imagery with the mixture-of-Gaussians model, while using an adaptive learning rate that is based on the decision of each spectral band. They also fuse the two spectral bands for their appearance model to increase the performance of target association. Torresan et al.15 perform the background subtraction on each individual spectral modality and merge the results by picking a master and slave foreground map based upon the confidence of each modality. By modeling each background pixel’s intensity as a single Gaussian distribution, Davis and Sharma12 extract regions-of-interest by the intersection of the visible and LWIR foreground maps. Salient contours from the regions-of-interest are then calculated from both visible and LWIR images and fused to create a single contour saliency map. The aforementioned works consider visible and LWIR bands; our algorithm additionally exploits near-infrared (NIR) and MWIR bands, and the combinations of spectral bands. Table 1 shows the spectral bands used and their associated wavelengths. The main contribution of this work is an algorithm to fuse multispectral data sets to reliably detect and track moving targets with high-probability and low-false alarm rate. We focus on detection and tracking of vehicles through an urban scene that includes partial occlusions and crowded traffic intersections. A block diagram of our proposed algorithm is shown in Fig. 1. To compensate for fluctuating pixel intensities in each spectral band, background models using a Gaussian mixture model (GMM) adapt to the evolving scenes and detect foreground pixels. Foreground pixels from different spectral bands are fused into a foreground region and filtered to obtain a single foreground map that represents pixel regions belonging to target candidates. Features based on the scale-invariant feature transform (SIFT) are extracted from these target regions and used for two purposes:19 detecting targets missed by the segmentation detection, and associating targets from a tracking database constructed from prior frames. Lastly, locations for each target are estimated and the GMM mixture is updated. Table 1Spectral band and their respective wavelengths.
To develop and evaluate the algorithm, we created a UAV imaging scenario that was synthetically generated from the digital imaging and remote sensing image generation (DIRSIG) toolset.20 DIRSIG is a mature and widely used simulation package for to wavelengths. An urban scene with 12 vehicles was simulated at visible, NIR, MWIR, and LWIR wavelengths. A normal traffic scenario was simulated using the open-source tool simulation of urban mobility (SUMO) to provide realistic traffic maneuvers. Figure 2 shows a frame from each spectral band. By visual inspection, the appearance of target vehicles varies between the scenes, providing different intensity information. Fig. 2Example multispectral frames from evaluated digital imaging and remote sensing image generation data set: (a) visible, (b) near-infrared (NIR), (c) midwave infrared (MWIR), and (d) long-wave infrared (LWIR).  The remainder of the paper is organized as follows: Sec. 2 presents the method for foreground extraction using the GMM and the region growing process to group disjoint pixels. We also discuss our method for fusing the spectral modalities in Sec. 2. Section 3 presents the association target candidates with track sequences. Experimental results on the performance of the algorithm are presented in Sec. 4. In Sec. 5, conclusions are presented. 2.Detection and Segmentation AlgorithmIn this section, we describe the detection and segmentation algorithms; we then present the fusion process used to combine foreground maps to build pixel regions that represent target candidates. Pixel intensities fluctuate due to changes in illumination and movement from both background and target objects. This does not allow a single value to characterize the time history of the intensity of a single pixel for a given video sequence. To compensate for these changes, background modeling techniques are used to describe the probability distribution of the pixels’ intensity by empirically deriving the parameters from the video sequence. The GMM has been successfully demonstrated to compensate for the fluctuations in pixel intensities.21–23 In a scene where the sensor is fixed, keeping the viewpoint stationary, we use statistical information extracted from the time history of the intensity fluctuations to understand the probability distribution of intensity at each pixel, and use these distributions to make hypotheses about the label of each pixel. Each pixel in the scene is classified as a foreground or background pixel, and we update the parameters of the GMM during each frame. We now describe this process in detail. We define as the pixel intensity at location and time . The goal is to classify this pixel as a background or foreground pixel by fitting it to a distribution model. The distribution of the time history of the intensity, , is modeled as a sum of weighted Gaussian distributions: where is the number of Gaussian distributions; is the mean of the distributions; and the covariance matrix, which is assumed to be diagonal, is given by , where is the identity matrix. The weighting factor represents the portion of which the ’th Gaussian that comprises the entire model, and is dependent on the number of occurrences for the particular distribution. This weighting has range , and is normalized such that . The Gaussian probability density function is From the distributions, it must be determined that the number of distributions are classified as belonging to the background. We select the top weighted distributions as the background, where The threshold Thr is user defined with range (0,1) and is dependent on the scene.In a complex scene with multiple moving targets where pixel distributions vary among targets, and among targets and background, more Gaussian models will be present and thus require higher Thr. In the scenes tested with this algorithm, few objects were moving and typically only one Gaussian mode was needed to describe the background. By executing the GMM algorithm with a series of parameters on the test data set, the optimal Thr was empirically derived for each spectral band by comparing correctly detected pixels to falsely detected pixels. The resulting values of Thr are shown in Table 2. In the algorithm, LWIR had the lowest Thr at 0.5, which is attributed to the distributions of the target intensities being similar, along with being lower than the background surrounding the targets. Table 2Gaussian mixture model parameters.
To evaluate whether the current pixel intensity is a background or foreground pixel, we calculate the a priori probability of that pixel intensity belonging to each of the distribution components. If the intensity value falls within 2.5 standard deviations of any background distribution, it is labeled background; otherwise, it is labeled as foreground. Following the classification of the pixel, the distribution parameters are updated as23 where is the learning rate. In a scene where objects typically move slowly, the update equations should also update at a slower rate and require a smaller . After the experimentation, we found the optimal for each data set as shown in Table 2. All spectral bands used a low , with the lowest value in the LWIR band, which can be attributed to no shadows being present.The GMM algorithm produces intermediate foreground maps in all spectral bands that do not represent the complete target region and do not necessarily correlate with one another. This is a consequence of discrepancies in the foreground modeling, and is caused by low SNR between the target and background. Examples of intermediate foreground maps at frame 600 are shown in Fig. 3. In the NIR band, the bottom target has a high number of foreground pixels in comparison with the other bands. In the MWIR band, the target on the left has a low number of foreground pixels whereas the other bands have a high number of pixels. The fusion of foreground maps from multispectral video creates combined foreground maps that accurately estimate the centroid of the target with a low-false alarm rate. This is distinct from previous efforts12–17 in that we have considered additional spectral bands for foreground fusion, and use SIFT features for unique target identification and detection of missed targets. We define a fused foreground map, , as the sum of individual weighted foreground maps, where represents the weighting and the subscript represents the respective band, is spatially filtered with a Gaussian filter with . Thresholding of is performed to remove pixels that have a low-foreground probability of belonging to the foreground, . The spectral combinations and their respective thresholds are shown in Table 3. Thresholds were chosen by the lowest false alarm rate produced by the detection algorithm. False alarm rates for the series of tested thresholds are presented in the Sec. 4 in Table 4. Table 3Spectral combinations and their respective background threshold.
Table 4False alarm rates produced for given thresholds.
Note: dashes (—) imply the threshold exceeded the maximum obtainable pixel value in the image. An example of a fused foreground is shown in Fig. 4(a). A smoothing of the combined foreground map is applied using a two-dimensional Gaussian filter and shown in Fig. 4(b). The filtering results in filling of gaps where pixels were missed from the foreground map without overdilating the region. The final foreground map is shown in Fig. 4(c). A zoomed area on a car region depicting the foreground fusion process is shown in Fig. 5. The effect of thresholding the fused and filtered foreground map is illustrated; the target shadow is removed from the foreground region. Fig. 4Fused foreground maps: (a) the fused foreground maps, ; (b) the foreground map after applying a Gaussian filter; and (c) the foreground after a threshold has been applied to the filtered image.  The final step of creating the pixel regions that represent the detected candidates is an image closing, which consists of a dilation followed by an erosion. The structuring element of this procedure is a disk with a radius of four pixels. The dilation operation fills in voids between pixel segments and grows the size of the region. In the erosion operation, we attempt to remove any unnecessary region growth that is a by-product of the dilation. Pixel regions that do not exceed an area of 200 pixels are filtered to remove the objects that may not represent vehicle-sized objects. 3.Target TrackingThe association of targets involves relating a track sequence from prior frames with target candidates detected in the current frame. This task is trivial in the case where targets stay separated and no occlusions exist. However, in actual practice and in this data set, targets become merged or occluded, making distinguishing between targets difficult. We have chosen to use SIFT features for identification due to their robustness with respect to changes in rotation and scale, and their invariance to change in camera viewpoints and illumination changes.19 Due to our reliance on these features to uniquely identify targets, we require them to be robust in long-term tracking applications. A disadvantage of SIFT is the heavy computations required for the keypoints, where typical processing times are tenths of seconds to multiple seconds per frame in a normal CPU implementation.24,25 Developments in graphics processing units (GPUs) and field programmable gate arrays (FPGAs) have created opportunities for real-time algorithms. SIFT implementations have been developed for both GPUs25–27 and FPGAs,24 where the results demonstrate real-time SIFT calculations. SIFT features are composed of a keypoint that gives subpixel location and orientation of the feature, along with a descriptor that is calculated based on local pixel texture. In the SIFT algorithm, keypoints are first identified at multiple scales. A scale space of the image is created with varying amounts of blur applied to each image using the Gaussian kernel. The blurred image is defined as where the Gaussian kernel with variance isWithin the scale space, difference of Gaussian (DoG) images are calculated by The local extrema in the DoG images at each scale are found by comparing the pixel value with its eight surrounding pixels and the nine neighboring pixels from each of the nearest blurred images. To create an invariance to scale, the extrema must exist on multiple scales. A filtering step of the detected extremas in the DoG images is implemented based on the intensity; an extrema with a low intensity is susceptible to changes in illumination and is therefore unstable and removed from the keypoints.A reference orientation for subsequent processing is given to the keypoint to provide invariance to rotation. From the blurred image in which the extrema was located, the gradient magnitude is calculated by and the orientation, , byA histogram of 10 deg bins is created of the orientations, and the magnitudes added to the histograms are the gradient magnitudes that are Gaussian weighted with a variance of . The peaks of the histograms are detected, where the highest peak and any peaks above 80% of the highest peak are selected as orientations for the new keypoints. Peaks in the histogram represent dominant directions of the local gradients. Unique identifications are generated for each keypoint, referred to as descriptors. A region around the keypoint, with respect to the calculated orientation, is divided into subregions. Gradient magnitudes and orientations are calculated for each pixel in these subregions, and histograms with 45 deg bins are calculated for each subregion. Through the use of a Gaussian weighting mask with of the descriptor window width (16 pixels for our case), points are inversely weighted proportional to their distance from the keypoint to decrease their contributions and reduce errors caused by window displacements. To match features from a tracked objects database to features from the current scene, a matching score is calculated by the Euclidean distance between two descriptors. The matching score between a tracked object and a frame object is calculated by where is the tracked object descriptor, is the frame object descriptor, and is the length of the descriptor vector, which is 128 for our case.The feature with the shortest Euclidean distance, i.e., the nearest neighbor, is selected as the matching feature. To remove matches that do not have a good match, a comparison is made between the nearest neighbor and the next nearest neighbor. If the ratio of the match scores between the nearest and the next nearest neighbor is , the match is rejected. Lowe19 found that this method rejects 90% of all incorrect keypoints and only removes 5% of the correct matches. Updating the track location is based on several factors. The search region for a matching target candidate is limited to the track’s estimated bounding box, preventing erroneous associations with targets of similar appearance but at a distance away. In the event that multiple targets are located in the track bounding box, such as at a road intersection when cars become merged, SIFT features are used to select the correct target. If no target is found in the bounding box, SIFT features are matched in the bounding box region and provide a velocity measurement for a linear motion model. Tracks are propagated if no target is matched and no SIFT features are found, a typical occurrence when the target may be partially or fully occluded from view of the sensor. The propagation projects the location of the bounding box linearly into future frames based on the most recent position and velocity prior to the occlusion. 4.ExperimentThe performance of this algorithm was evaluated with a synthetically generated data set using the DIRSIG toolset.20 A standard midlatitude summer model was used for the atmospheric model MODTRAN.28 The thermal signatures for 12 vehicles were simulated with the thermal prediction software MuSES.29 Realistic traffic patterns were generated using the SUMO traffic simulator.30 The video sequence consists of 600 frames of sampled at . The ground sample distance is 0.0635 m and frames are coaligned where pixels correspond geometrically between frames and registered between the spectral bands. As this is a synthetically generated data set, the locations of pixels corresponding to each vehicle is known, providing ground truth centroids of vehicles in the scene. 4.1.DetectionWe now present the performance for detecting moving targets using our fusion algorithm applied to the DIRSIG data set. For the evaluation of segmented detection rates, a successful detection is a group of pixels that has a centroid with a Euclidean distance within 0.95 m of the centroid of a ground truth object; otherwise, it is considered a false alarm. False alarms are reported on a per frame basis. Targets occluded by 20% or more are not factored into the target detection score. False alarm rates for a series of examined thresholds are shown in Table 4, where the optimal thresholds are given in bold. The false alarm rate is presented by the number of false alarms per frame. The optimal thresholds for image filtering were selected by choosing the lowest false alarm rate for their respective spectral combination. LWIR resulted in the highest false alarm rate at 1.30. Three of the fusion combinations have false alarms less than 1: MWIR–LWIR, VIS–NIR–MWIR, and NIR–MWIR–LWIR. MWIR–LWIR presented the lowest false alarm rate of 0.96. In the single spectral bands, NIR had the lowest false alarm rate with 1.07. Detection rates by segmentation for a series of examined thresholds are shown in Table 5, where the results for the optimal thresholds for each spectral combination are given in bold. LWIR achieved the highest detection rate of 0.94 and VIS had a detection rate of 0.93. VIS–MWIR and VIS–LWIR resulted in detection rates of 0.93, while the weighted VIS–NIR–MWIR–3*LWIR (TOT3) and VIS–LWIR3 had results of 0.91 and 0.92, respectively. Table 5Detection rates produced for given thresholds.
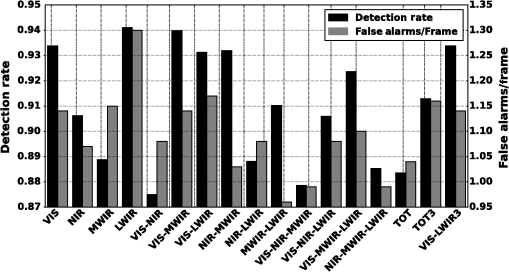
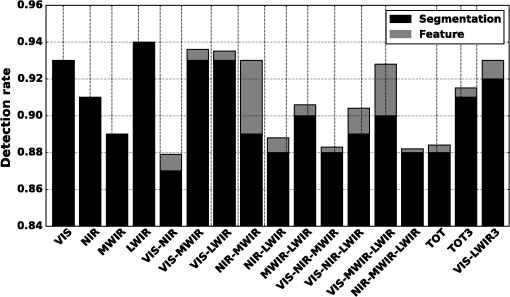
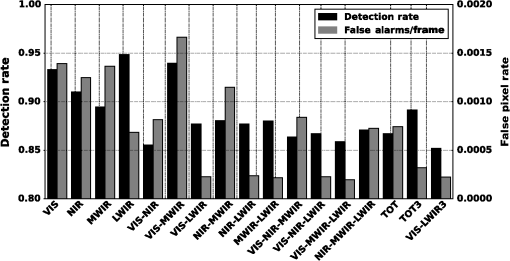
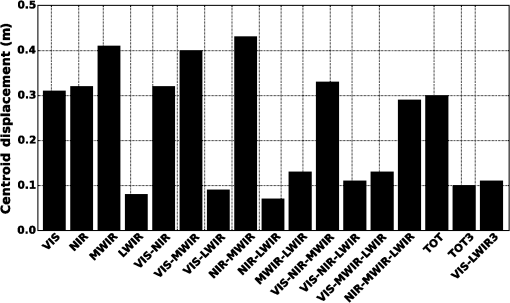
Note: dashes (—) imply the threshold exceeded the maximum obtainable pixel value in the image. Total detection rates and false alarm rates are shown in graph form in Fig. 6. The total detection rates include detections by both segmented objects and features. In the single spectral bands, LWIR resulted in a detection rate of 0.94, but suffered from the highest false alarm rate of 1.30. The detection rate of VIS was slightly lower at 0.93, but lowered the false alarm rate to 1.14. VIS–MWIR had a detection rate of 0.94, while lowering the false alarm rate to 1.14. MWIR–LWIR produced the lowest false alarm rate at 0.96 with a detection rate of 0.91. These presented fusion results demonstrate that fusing multiple spectral bands lowers false alarms while maintaining high detection rates. The contribution to the overall detection by segmented objects and features is shown in Fig. 7. The black bar indicates the rate by segmented detection and the gray bar is the additional detection rate by using the SIFT features. Detection by segmentation is the primary detection mechanism and contributes to the bulk of the detection rate, whereas feature detection is secondary and has a smaller impact on the overall detection rate. Pixel texture varies in each spectral band, providing different spatial features that are independent of one another. Extracting features from different spectral bands provides additional features for tracking and identification. Single spectral bands did not have any detection by features, which we attributed to an insignificant number of features to match between the target database and the scene. NIR–MWIR had the highest contribution for detections by features at 0.040. We attributed this to the high number of false pixels that were detected by segmentation, incorporating features that belong to the background. VIS–MWIR–LWIR had the next highest contribution of feature detections with 0.028. The overall detection contribution by features is not significant for this data set, but provides a means to track targets in difficult situations such as busy intersections or partial occlusions when they would otherwise be lost. Algorithm performance for estimating the targets true centroid by correctly detecting pixels that belong to ground truth objects will now be discussed. A correctly detected pixel is defined as belonging to a ground truth object; otherwise, it is classified as a false pixel. A pixel scoring example is shown in Fig. 8. Figure 8(a) is a ground truth vehicle in MWIR and Fig. 8(b) is labeled as foreground pixels. Blue pixels represent true positives that belong to the ground truth object, and red pixels represent pixels that were falsely detected. For this example, false pixels are attributed to the vehicle shadow. Fig. 8Example showing how detected pixels are scored as true positives or false alarms: (a) an example vehicle in MWIR; (b) detected foreground pixels; blue indicates true positive and red indicates false alarm. 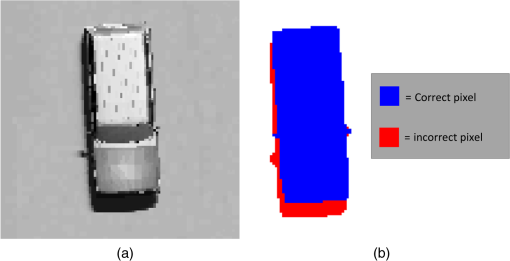 We define the pixel detection rate for the full video sequence as where is the number of frames. High pixel detection rates result in accurate estimates of target centroids, but falsely detected pixels can negatively affect the centroid calculation, resulting in less accurate results. The false pixel rate is measured per frame and presented as where is the number of nontarget pixels in the frame and is the number of frames.Pixel detection rates and false pixel rates for all spectral bands and fusion combinations are shown in Fig. 9. LWIR produced the highest pixel detection rate of 0.95 and a false pixel rate of 0.0007. The fusion combination VIS–MWIR produced a high pixel detection rate of 0.94, but suffered the highest false pixel rate of 0.0017. TOT3 resulted in a detection rate of 0.89 and false pixel rate of 0.0003. Seven fusion combinations resulted in false pixel rates . Displacement error between detected objects and their respective ground truth centroids is a measure of how accurately an algorithm estimates the true centroid of the target. For target tracking, centroids are input to filters that predict future targets locations, i.e., Kalman filtering, which require accurate estimates. Displacements of detected targets over all frames were measured and the root-mean-square error (RMSE) was calculated as where are the coordinates of the measured centroid, are the ground truth centroids, and is the number of detections. The results are presented in Fig. 10. NIR–LWIR had an RMSE of 0.07 m, which was the lowest for all spectral combinations. LWIR had the next lowest RMSE at 0.08 m, whereas the other single spectral bands had errors . The fusion results presented highlight the centroid accuracy improvements made by fusing spectral bands as compared with using single bands.4.2.TrackingWe now evaluate the performance of the fusion algorithm to associate targets between scenes and create a tracking profile using the foreground combination map (VIS–LWIR). This weighted combination was chosen due to the low centroid error, along with the high detection rate and low-false alarm rate. In this evaluation, the bottom 400 rows of pixels are not considered for the tracking results due to trees obstructing the view of the imaging sensors, preventing full vehicle segmentation. Sample images from the tracking sequence are shown in Fig. 11. The yellow box indicates the track algorithm has used a segmented object to update the track location. A teal box indicates that no segmented object matched and SIFT features were used to update the track location. Fig. 11Single frames from the tracking sequence: (a) frame 150, (b) frame 300, (c) frame 450, and (d) frame 600. (Video 1, MPEG, 14 MB [URL: http://dx.doi.org/10.1117/1.OE.54.12.123106.1]).  The motion of 12 vehicles was simulated for an urban traffic environment. Tracks were initiated on all 12 vehicles during the video. Of those 12 vehicle tracks, 11 were tracked though the entire video sequence with no errors. Due to being idle for extended periods of time, one track was lost, but a new track was initiated after it initiated movement. There were no instances where track identities were switched between vehicles and only one instance of a false track. Three false tracks were produced, where two false tracks are attributed to the idle vehicle. The tracking results are summarized in Table 6. Table 6Results of vehicle tracking.
5.ConclusionIn this paper, we proposed an algorithm to fuse multispectral data sets to increase detection accuracy of a video tracker, while maintaining a high detection rate and low-false alarms per frame. Previous works consider visible and LWIR data sets;12–17 we extend previous work to include NIR and MWIR. In these four spectral bands, we build a GMM to detect foreground pixels by modeling the time history of the pixels intensities. Foreground pixels from all spectral bands are weighted and fused into foreground maps, and formed into targets candidates. Target candidates are tracked through the frame sequence using SIFT features to track missed detections and uniquely identify targets. Our proposed algorithm was tested on synthetically generated data using the DIRSIG toolset of visible, NIR, MWIR, and LWIR imagery. Compared with the single spectral band base, the fused algorithm improves detection accuracy while improving detection rates and lowering false alarm rates. The detection results provided input to a video tracker that detected the 12 moving vehicles in the scene. Of those 12 targets, 11 were tracked with no failures, one vehicle showed track-loss, but this track was reinitiated, and three false tracks occurred. AcknowledgmentsThis paper has been approved for public release by the Air Force, Case No. 88ABW-2015-0296, date: January 27, 2015. This work was sponsored by the Air Force Research Laboratory, Contract No. FA8750-12-2-0108. The views and conclusions contained herein are those of the authors and should not be interpreted as necessarily representing the official policies or endorsements, either expressed or implied, of Department of the Air Force, Air Force Research Laboratory, or the U.S. Government. We would like to thank Brian Wilson and Michigan Tech Research Institute for generating the DIRSIG data sets used in this work. ReferencesF. Heintz, P. Rudol and P. Doherty,
“From images to traffic behavior—a UAV tracking and monitoring application,”
in 10th Int. Conf. on Information Fusion,
1
–8
(2007). http://dx.doi.org/10.1109/ICIF.2007.4408103 Google Scholar
L. Meng and J. P. Kerekes,
“Object tracking using high resolution satellite imagery,”
IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens., 5
(1), 146
–152
(2012). http://dx.doi.org/10.1109/JSTARS.2011.2179639 Google Scholar
P. Liang et al.,
“Spatial context for moving vehicle detection in wide area motion imagery with multiple kernel learning,”
Proc. SPIE, 8751 875105
(2013). http://dx.doi.org/10.1117/12.2015967 PSISDG 0277-786X Google Scholar
K. S. Kumar et al.,
“Visual and thermal image fusion for UAV based target tracking,”
MATLAB - A Ubiquitous Tool for the Practical Engineer, 307 2011). Google Scholar
H. Choi and Y. Kim,
“UAV guidance using a monocular-vision sensor for aerial target tracking,”
Control Eng. Pract., 22 10
–19
(2014). http://dx.doi.org/10.1016/j.conengprac.2013.09.006 COEPEL 0967-0661 Google Scholar
K. Beier and H. Gemperlein,
“Simulation of infrared detection range at fog conditions for enhanced vision systems in civil aviation,”
Aerosp. Sci. Technol., 8
(1), 63
–71
(2004). http://dx.doi.org/10.1016/j.ast.2003.09.002 Google Scholar
H. Li, B. Manjunath and S. K. Mitra,
“Multisensor image fusion using the wavelet transform,”
Graph. Models Image Process., 57
(3), 235
–245
(1995). http://dx.doi.org/10.1006/gmip.1995.1022 Google Scholar
A. Ardeshir Goshtasby and S. Nikolov,
“Image fusion: advances in the state of the art,”
Inf. Fusion, 8
(2), 114
–118
(2007). http://dx.doi.org/10.1016/j.inffus.2006.04.001 Google Scholar
J. Nunez et al.,
“Multiresolution-based image fusion with additive wavelet decomposition,”
IEEE Trans. Geosci. Remote Sens., 37
(3), 1204
–1211
(1999). http://dx.doi.org/10.1109/36.763274 IGRSD2 0196-2892 Google Scholar
S. Li, B. Yang and J. Hu,
“Performance comparison of different multi-resolution transforms for image fusion,”
Inf. Fusion, 12
(2), 74
–84
(2011). http://dx.doi.org/10.1016/j.inffus.2010.03.002 Google Scholar
Q.-G. Miao et al.,
“A novel algorithm of image fusion using shearlets,”
Opt. Commun., 284
(6), 1540
–1547
(2011). http://dx.doi.org/10.1016/j.optcom.2010.11.048 OPCOB8 0030-4018 Google Scholar
J. W. Davis and V. Sharma,
“Background-subtraction using contour-based fusion of thermal and visible imagery,”
Comput. Vision Image Understanding, 106
(2), 162
–182
(2007). http://dx.doi.org/10.1016/j.cviu.2006.06.010 CVIUF4 1077-3142 Google Scholar
C.-Y. Chen and W. Wolf,
“Background modeling and object tracking using multi-spectral sensors,”
in Proc. of the 4th ACM Int. Workshop on Video Surveillance and Sensor Networks,
27
–34
(2006). Google Scholar
A. Leykin and R. Hammoud,
“Pedestrian tracking by fusion of thermal-visible surveillance videos,”
Mach. Vision Appl., 21
(4), 587
–595
(2010). http://dx.doi.org/10.1007/s00138-008-0176-5 MVAPEO 0932-8092 Google Scholar
H. Torresan et al.,
“Advanced surveillance systems: combining video and thermal imagery for pedestrian detection,”
Proc. SPIE, 5405 506
–515
(2004). http://dx.doi.org/10.1117/12.548359 PSISDG 0277-786X Google Scholar
Z.-J. Feng et al.,
“Infrared target detection and location for visual surveillance using fusion scheme of visible and infrared images,”
Math. Prob. Eng., 2013 720979
(2013). http://dx.doi.org/10.1155/2013/720979 Google Scholar
L. Xiaoqi et al.,
“The infrared and visible image fusion algorithm based on target separation and sparse representation,”
Infrared Phys. Technol., 67 397
–407
(2014). http://dx.doi.org/10.1016/j.infrared.2014.09.007 Google Scholar
D. Scribner, P. Warren and J. Schuler,
“Extending color vision methods to bands beyond the visible,”
in Proc. IEEE Workshop on Computer Vision Beyond the Visible Spectrum: Methods and Applications (CVBVS’99),
33
–40
(1999). Google Scholar
D. G. Lowe,
“Distinctive image features from scale-invariant keypoints,”
Int. J. Comput. Vision, 60
(2), 91
–110
(2004). http://dx.doi.org/10.1023/B:VISI.0000029664.99615.94 IJCVEQ 0920-5691 Google Scholar
J. S. Sanders and S. D. Brown,
“Utilization of DIRSIG in support of real-time infrared scene generation,”
Proc. SPIE, 4029 278
–285
(2000). http://dx.doi.org/10.1117/12.392535 PSISDG 0277-786X Google Scholar
C. Stauffer and W. E. L. Grimson,
“Adaptive background mixture models for real-time tracking,”
in IEEE Computer Society Conf. on Computer Vision and Pattern Recognition,
(1999). Google Scholar
P. KaewTraKulPong, R. Bowden,
“An improved adaptive background mixture model for real-time tracking with shadow detection,”
Video-Based Surveillance Systems, 135
–144 1st ed.Springer, New York City
(2002). Google Scholar
Z. Zivkovic,
“Improved adaptive Gaussian mixture model for background subtraction,”
in Proc. of the 17th Int. Conf. on Pattern Recognition (ICPR) 2004,
28
–31
(2004). Google Scholar
L. Chang et al.,
“FPGA-based detection of sift interest keypoints,”
Mach. Vision Appl., 24
(2), 371
–392
(2013). http://dx.doi.org/10.1007/s00138-012-0430-8 MVAPEO 0932-8092 Google Scholar
H. Fassold and J. Rosner,
“A real-time GPU implementation of the sift algorithm for largescale video analysis tasks,”
Proc. SPIE, 9400 940007
(2015). http://dx.doi.org/10.1117/12.2083201 PSISDG 0277-786X Google Scholar
C. Wu,
“SiftGPU: a GPU implementation of scale invariant feature transform (SIFT),”
(2007). Google Scholar
S. N. Sinha et al.,
“Feature tracking and matching in video using programmable graphics hardware,”
Mach. Vision Appl., 22
(1), 207
–217
(2011). http://dx.doi.org/10.1007/s00138-007-0105-z MVAPEO 0932-8092 Google Scholar
A. Berk, L. S. Bernstein and D. C. Robertson,
“MODTRAN: a moderate resolution model for lowtran,”
Massachusetts
(1987). Google Scholar
K. Johnson et al.,
“Muses: a new heat and signature management design tool for virtual prototyping,”
in Proc. of Ninth Annual Ground Target Modeling and Validation Conf.,
(1998). Google Scholar
M. Behrisch et al.,
“Sumo-simulation of urban mobility-an overview,”
in SIMUL 2011, The Third Int. Conf. on Advances in System Simulation,
55
–60
(2011). Google Scholar
BiographyCasey D. Demars received his BS and MS degrees in electrical engineering from Michigan Technological University in 2010 and 2012, respectively, and currently he is pursuing his PhD in electrical engineering from Michigan Technological University. From 2010 to 2012, he was employed by Calumet Electronics Corporation as the technical lead in establishing prototype and testing capabilities for optical polymer waveguides. His PhD research focus is on detection and tracking by exploiting heterogeneous sensor data, particularly multispectral imagery. He is a student member of IEEE and SPIE. Michael C. Roggemann is a professor of electrical engineering at Michigan Technological University. He joined Michigan Tech in 1997. Prior to joining Michigan Tech, he was a USAF officer who is now honorably retired. He took his BSEE degree in 1982 from Iowa State University, and his MSEE and PhD degrees from the Air Force Institute of Technology in 1983 and 1989, respectively. He is a fellow of the SPIE and OSA. Timothy C. Havens received his MS degree in electrical engineering from Michigan Technological University, Houghton, in 2000 and the PhD degree in electrical and computer engineering from the University of Missouri, Columbia, in 2010. He was an associate technical staff with MIT Lincoln Laboratory from 2000-2006. He is currently the William and Gloria Jackson assistant professor with the Departments of Electrical and Computer Engineering and Computer Science at Michigan Technological University. |