|
|
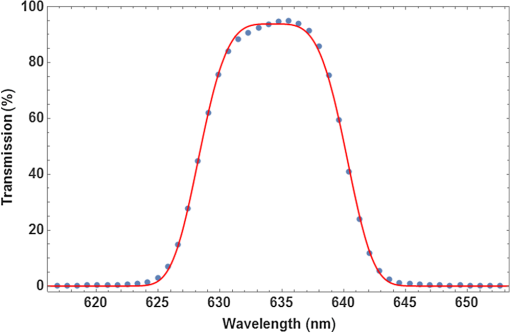
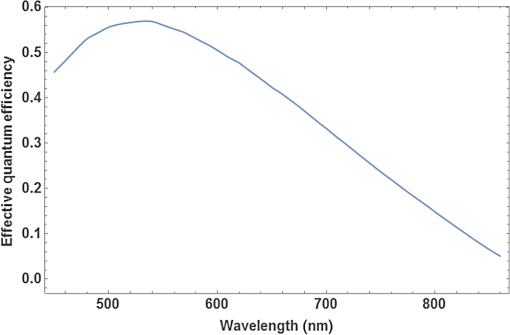
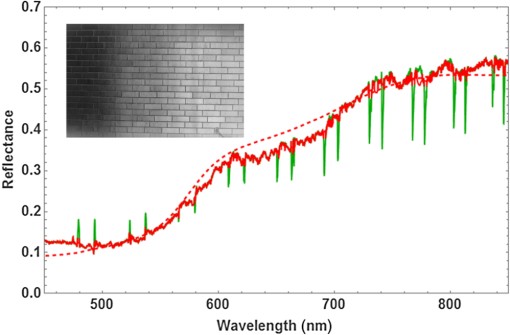
1.IntroductionMultispectral and hyperspectral imaging systems deliver valuable products to users in areas such as agriculture, mining, environmental monitoring, disaster assessment, and military reconnaissance. The rapid development toward low weight and affordable systems opens up a multitude of small scale applications using both ground-based and miniature unmanned aerial vehicle (UAV)-based systems. As the typical payload for mini-UAVs is 2 to 3 kg, a design goal for a hyperspectral imaging system must also be to make this technology adaptable to these smaller sensor platforms. In many current system designs, especially in the grating-based imaging spectrometer solutions, spectral resolution is given precedence over spatial resolution in the use of detector elements available. Since the spectral signature depends on the spatial resolution, especially for textured surfaces, the information content can be higher when the spatial resolution is given priority.1 The optimal trade-off depends on target range and target size as well as the spectral variability of the target and background materials. Solid materials mostly exhibit slow spectral variations and can, therefore, be more sparsely sampled. An example in which high spatial resolution is needed is the detection of intercropped plants, e.g., cannabis with maize, or in the detection of plastic litter in coastal regions. Conventional hyperspectral sensors tend to be rather bulky and heavy. The wavelength separation mechanism often relies on dispersive or interferometric elements in combination with several sets of collimating and reimaging optics. New more compact systems are being developed to meet the requirements of low size, weight, power consumption, and cost, which includes both push-broom solutions and snapshot systems.2–11 In the design presented here, high spatial resolution is achieved by mounting a linear variable filter (LVF) on top of a large focal plane array (FPA) with (22.3 MP). The LVF covers a range of 450to 880 nm in the visible- and near-infrared spectral region. The idea to combine an imaging FPA with an LVF is not new. The technology has already been described12 and tested.13–15 Previous problems with LVF fabrication errors and off-axis wavelength shifts are addressed in the present solution using signal processing. Furthermore, the excellent transmission properties and spectral profile of the developed LVF decrease the problems associated with radiation scattered off the FPA. Large LVF allows the use of very large FPAs with corresponding advantages both with respect to production rate, i.e., covering large areas in a short time, and adaptability to new sensor developments. Simultaneously, it is difficult to obtain a full spectral octave or more using interference filter technology. The present filter is the first filter in this development that achieves almost one full octave. The transmission is also tailored to form close to constant transmission over a short spectral range—top hat shape rather than the typical Lorentzian shape. In the next section, the camera design is described followed by the characterization of the LVF and wavelength calibration. Experimental results are shown using the camera as a field spectrometer and as a high spatial resolution hyperspectral imager. Finally, some conclusions are given. 2.Hyperspectral Camera DesignIn the present design, an LVF is placed in front of a full-frame sensor FPA. The positioning of the filter is shown in Fig. 1. A full format camera, i.e., with an FPA size of , was found easiest to match with the size of the current LVF. The camera used in the current setup is a modified Canon EOS 5D Mark III, where the Bayer filter, the infrared blocking filter, and the antialiasing filter have been removed.16 The camera exhibited some nonuniformity due to incomplete removal of the Bayer filter, but this is taken into account by a nonuniformity correction of the FPA. Fig. 1Illustration of a FPA fitted with a LVF and a lens. The coordinate system is centered on the FPA. 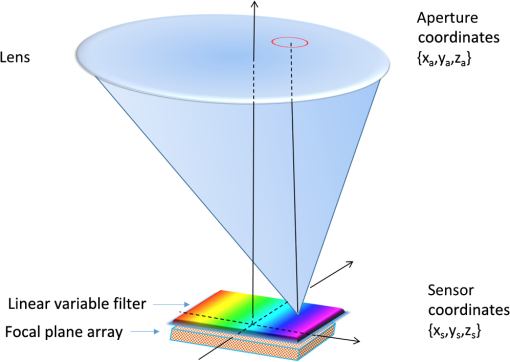 Canon 5D allows images to be recorded in 14-bit RAW format. A consumer camera was selected since all electronics and software needed, including image compression, are built into the camera in a cost-effective way. Due to the small weights associated with the filters involved, there is no difference in weight between the original consumer camera and the hyperspectral camera. The weight of the camera, currently 860g (lens excluded), could in principle be lowered further since the optical seeker is not needed. The camera is currently equipped and calibrated with tilt/shift-lenses, which are color-corrected over the visible spectral range. Outside the visible spectral region, the change in focal length is compensated for by tilting the optics. This is of course a compromise since the focal length does not vary linearly with the wavelength. This was found to be the best solution in terms of image quality after comparison with other lenses that were chromatically corrected for the full spectral region. Currently, the camera has two lens options with focal lengths 45 and 90 mm, both with -number 2.8. The choice of lens depends on the field-of-view (FOV) required. The design has some potential drawbacks with respect to scattering between the FPA and the filter.17 The effective filter transmission and spectral profile also depend on the distance between the FPA and the filter, filter bandwidth, and -number of the lens. This efficiency variation has, therefore, been studied more closely and is modeled below. 3.Filter and Camera Characterization3.1.Filter CharacterizationHere, the LVF is discussed as a separate component. In an LVF, also known as a wedge filter, the thickness of the coating varies linearly over the length of the filter, resulting in a linear and continuous variation in the transmitted wavelength. A high spectral gradient, i.e., a large spectral range over a short distance, is desirable since it allows the use of smaller and less expensive FPAs. This is, however, difficult to achieve in practice. The full format FPAs also have the advantage of high spatial resolution over a large FOV combined with high sensitivity. Typical for an LVF, the bandwidth is a constant fraction of the center wavelength. For the present filter, the bandwidth is of the center wavelength and the peak transmission varies in the range 65% to 95%,18 see Fig. 2. The number of uncorrelated spectral bands for the present filter is over the spectral range 450 to 880 nm. Both the filter transmission and camera responsivity are decreasing for wavelengths below 550 nm. This is also coincident with decreasing solar irradiance in this spectral region. It is, therefore, important to achieve high filter transmission also at shorter wavelengths. The nature of the losses in this spectral region is not well understood and is an area for improvement. Fig. 2Transmission of the filter for the spectral region 450 to 880 nm sampled at 10 different wavelengths. Measurements of linear variable bandpass filter by courtesy of delta optical thin film A/S. 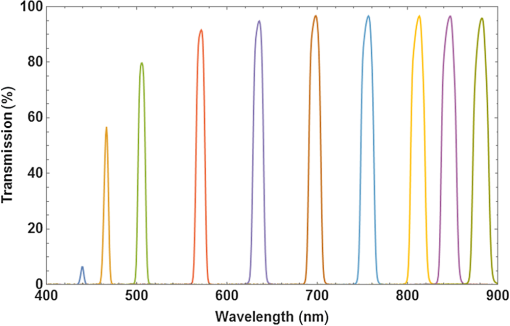 The filter bandwidth can be measured by using collimated monochromatic illumination of a narrow slit aligned perpendicularly to the linear variation along the spectral axis direction. The shape of the band-pass filter depends on the physical processes involved. Here, the bandpass transmitted signal is fitted to a generalized Gaussian distribution according to and where is the profile of the transmission of monochromatic radiation at and the spectral bandwidth is the full width at half maximum. A measurement centered on 634.3 nm has been fitted and is shown in Fig. 3.3.2.Camera CharacterizationHere, the camera characteristics including the LVF are discussed. The LVF is positioned close to the cover glass and a distance of 2.1 mm from the FPA to lower the effect of interfering multiple scattering between the components. In Fig. 4, the radiation distribution on the filter is illustrated for a monochromatic point source. It is clear that a trade-off must be made with respect to the size of the illuminated spot on the filter, the bandwidth of the filter, and the filter linear variation along the spectral axis. While the filter linear variation along the spectral axis and bandwidth are inherent filter properties, the illuminated spot is determined by the optics. The trade-off is matched to the spectral resolution and system sensitivity needed in the intended application. If the filter bandwidth is broad, the transparent area will be larger than the illuminated spot and the signal will be high due to efficient use of the illuminating spot and the large filter bandwidth. Broadband solutions sacrifice spectral resolution but might be needed in low-light applications. If the bandwidth is narrow, the transparent area will be smaller than the illuminated spot. Narrowband solutions increase the spectral resolution at the cost of lowering the filter efficiency. With exchangeable filters, if available, the spectral properties could be selected with respect to the task. In the present design, moderate spectral resolution was selected to obtain good performance with respect to the spectral content of ordinary solid targets. Fig. 4LVF positioned at a distance above the FPA. The illuminated area from a point source is illustrated in relation to the spectrally transparent slit formed by the LVF. 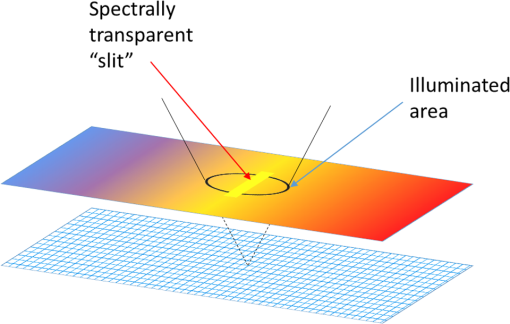 Although it is desirable to use collimated radiation at the filter, the present application requires the light path to be nonparallel and with cone-shaped incident radiation. The angle of incidence will vary with the position on the FPA and with the aperture position of the lens.19 A mathematical model for the transformations is developed to obtain an understanding of the camera design. The model uses numerical integrations and can be realized for different -numbers and FPA positions. First, the spectral shifts due to the variation in angle of incidence are discussed. Second, the integrated effect of these shifts is derived for a specific pixel due to the variation over the aperture. The angular-dependent spectral transmission of the LVF will cause a spectral shift both along the direction of the spectral axis and perpendicular to this direction. The wavelength scale, therefore, has to be calibrated with respect to the spectral shifts due to the varying angle of incidence. The wavelength shift effect due to the span of angles is expected to be less or similar to the filter bandwidth. Equally important is the scaling factor due to the distance between the filter and the FPA. Both phenomena can be corrected for in the calibration process. The wavelength interference shift due to angular variation is given by20 where is the angle of incidence, is the refractive index of the filter, and is the wavelength at normal incidence (i.e., ). The shift due to change in angle of incidence is shown in Fig. 5. The index of refraction was set to 1.56 in this example.Fig. 5Wavelength shift due to changes in angle of incidence. Transmission of the filter at normal incidence for the center wavelength 785 nm is shown as a solid blue line, in which a relative bandwidth of 2% was used. Transmission profiles are shown for the angles of incidence 0, 5, 10, and 15 deg. 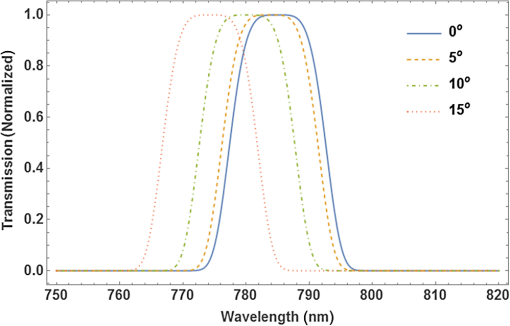 When the LVF is used in the current camera design, the light will be incident at each FPA position with a range of different angles as determined by the opening of the lens aperture. By introducing a coordinate system centered on the FPA, as shown in Fig. 1, the shifted center wavelength is determined from where and are the FPA and aperture coordinates, respectively, the -coordinate has been replaced by , is the filter dispersion (spectral gradient of the LVF), is the focal length of the lens, and is the distance between the LVF and the FPA.The transmitted signal for each position of the FPA is then obtained by integrating the radiance over the normalized aperture where the aperture normalization is given byObserve that given by Eq. (1) is a function of aperture coordinates through the dependency of , as in Eq. (4). The integral does not have a closed solution and has to be integrated numerically. In this camera model, some angular effects of minor importance, such as surface projections, have been ignored. The model has proven to still be quite accurate and can be used for arbitrary sensor positions and -numbers. Stray light is discussed in a reference,2 but no analytical expression is given. The scattered radiation is modeled here by adopting a skewed normal distribution multiplied by the filter reflectance. The model is based on the idea that the source of scattering originates in the region where the filter is partially transmitting and partially reflecting the radiation. The scattered radiation is assumed to diffuse out of this region tempered by filter and sensor reflectance. The complementary error function (Erfc) is adopted as a solution to the diffusion process. The original transmission model in Eq. (1) is, therefore, modified and is now given by where is the scattering amplitude, is the diffusion parameter due to reflectance in the FPA, and is a skew parameter that takes the overall angle of incidence into account, i.e., it varies with the position along the spectral axis. Erfc is the complementary error function. Only radiation scattered into the reflective part of the filter is contributing to the signal.Some example results for constant exposure are shown in Fig. 6, with the model parameters as listed. With the filter position at a distance of 2.1 mm from the FPA, some efficiency losses are observed at -number 2.8, as can be seen from the decreasing peak signal in Fig. 6. It could, therefore, be beneficial to place the filter closer to the FPA when larger apertures are being considered. At -number 8, the actual transmission is close to that shown in Fig. 2. Fig. 6Transmission as a function of position as defined in Fig. 1 for input radiation at wavelength 785 nm. The blue curve (upper peak) is for -number 8, and the red curve (lower peak) is for -number 2.8 (data are scaled relative to the maximum of the blue data points). The shaded areas represent radiation backscattered from the FPA and trapped between the FPA and the LVF. It was found to be 9.5% for -number 8% and 9.2% for -number 2.8. 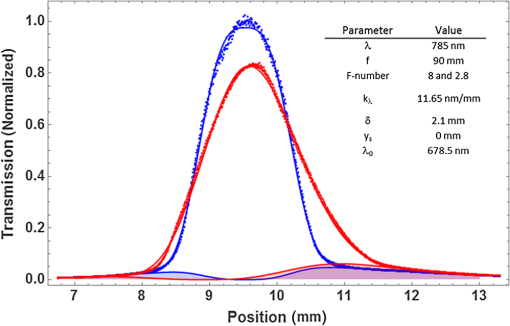 4.Spectral and Radiometric CalibrationSpectral calibration of the hyperspectral camera has been performed at four different laser wavelengths: 543, 594, 632.8, and 785 nm. The calibration was performed by recording stationary (nonscanned) images using a laser-illuminated integrating sphere (from Sphere Optics). At the wavelength calibration of the LVF component, some nonlinearity was observed. The positions of the center of gravity of the camera responses due to these laser lines were, therefore, fitted to a second-order polynomial taking this nonlinearity in the filter dispersion into account. The wavelength accuracy of the fitted polynomial is found to be for the laser lines measured. Due to the angle dependencies of light transmission through the LVF, there will be a small dependency on both focal length and -numbers while a calibration look-up table has to be created with respect to those parameters. Radiometric calibration is conveniently made using camera signal in digital numbers (DN). The camera reading depends on the number of electrons required to fill the well. For the present 14-bit camera, the full well corresponds to 68,900 electrons.21 At ISO 100, this corresponds to a gain of . At higher ISO, only a fraction of the well corresponds to the maximum signal, with a corresponding change in gain. At ISO 400, the gain is . Assuming a linear sensor, the camera reading in DN for pixel position can be written as where is the gain at the current ISO setting, is a parameter taking sensor quantum efficiency and other losses into account, is the effective radiance as filtered at the local FPA position, is the solid angle of the sensor element, is the aperture area, is the exposure time, and is an effective offset while and are Planck’s constant and the speed of light, respectively.Observe that the transmission wavelength of the LVF will be position dependent, in practice, a function of the image column. The effective radiance is obtained from where is the local transmission of the LVF at position .The camera was radiometrically calibrated using an integrating sphere (from Sphere Optics) illuminated by a calibrated halogen broadband light source. The camera exhibited some residual losses due to incomplete removal of the Bayer filter and a small variation due to transmission variation of the LVF, which was taken into account in the nonuniformity correction of the FPA. Results are shown in Fig. 7, where data were fitted to a fourth-order polynomial, which is subsequently used for the nonuniformity correction. Fig. 7Signal obtained at ISO 400 from the calibrated integrating sphere, where the red smooth curve is a polynomial fit to image data obtained by using the integrating sphere. 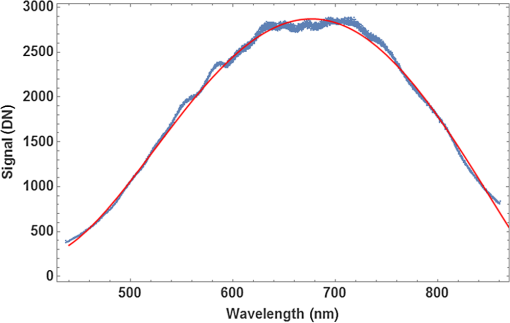 Using the knowledge of the calibrated spectrum from the integrating sphere, the effective quantum efficiency of the camera (including optical losses) was calculated and is shown in Fig. 8. In the radiometric calibration, the camera signal DN is translated to radiance. The radiance is obtained by comparing an offset corrected target measurement with a corresponding offset corrected reference measurement adjusted for the camera settings and multiplied by the calibrated reference radiance as given in the following equation: 5.Camera as a Field SpectrometerThe spectral fidelity of the sensor system is of major importance when using spectral measurements for material classification. The common procedure is to try to measure the spectral properties of homogeneous materials or to average the spectrum over local textures assuming those textures are not spatially resolved. Using the present system, textures can be analyzed and outliers excluded. Reference spectra at different spatial resolutions can be estimated. This is an area that will be further explored, but some examples are given below. It is a great advantage to be able to record reference spectra with the same type of equipment that is used in the remote sensing application. By doing so, artifacts are automatically compensated for. The so-called end members representing the constituents of the scene are the desired reference objects. Even when performing in situ measurements, end members can be hard to identify. It is, therefore, important to document the type of material that is being used when recording reference spectra. The material can also exhibit a texture at high spatial resolution that is mixed together at lower resolution in varying degrees. When imaging a small region for the purpose of obtaining the spectrum of the materials, the area has to be uniform from the perspective that the statistical variation should be constant over the patch. Such an area could be, for example, a patch of a grass field or a part of a wall. The spectral variability over the scene can be used to distinguish between the contributing materials. Examples of this approach will be given below. First, the radiance obtained from solar irradiance reflected from a white reference panel close to normal is shown in Fig. 9. Equation (10) was used to calculate the spectral radiance. The MODTRAN result shown for comparison was obtained using a subarctic summer atmosphere model, a rural aerosol model (with visibility 50 km), and a solar zenith angle of 40 deg (which corresponded to the time of acquisition). The MODTRAN spectrum was convolved with the wavelength-dependent bandwidth obtained for the LVF, to enable comparison at similar spectral resolutions. Fig. 9Solar irradiance reflected from a white panel close to normal used as reflectance reference. The red thin curve is solar radiance calculated using MODTRAN. The blue curve is the measured reflected solar radiance. 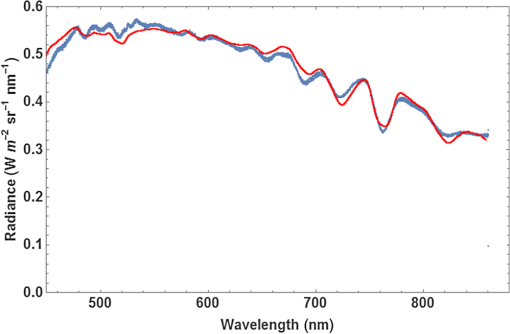 Detection of vegetation using the unique spectral characteristics of chlorophyll is a common task, as in health quality checks for agricultural monitoring as well as in camouflage detection for military reconnaissance. It is important for the instrument to truthfully be able to reproduce the variability in chlorophyll content and other constituents in the vegetation. The spectral reflectance of a newly cut lawn is shown as an example in Fig. 10. There are small variations in the spectrum, not only due to variation in the type of vegetation but also with respect to the relative angle with respect to the solar illumination. In this example, the angle between the direction of illumination and direction of imaging is in azimuth. Measurement is compared to data obtained from the ASTER spectral library.22 Fig. 10Grass spectrum obtained from newly cut field (see inset) using a white panel as a reference. The spectral median value has been obtained using several rows in the image. Dashed red line is a reference spectrum from the ASTER database. 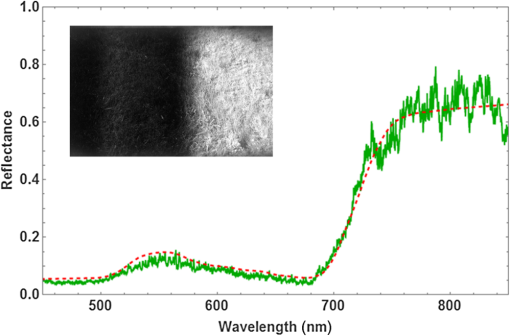 The second example shown in Fig. 11 is the spectrum of a red brick wall. Mapping three-dimensional (3-D) buildings is an example where this is of interest. Here, the influence of texture can be clearly seen. By performing a statistical analysis of the spectrum as a function of wavelength and position, the brick spectrum can be separated from the spectrum of the joints between the bricks. 6.Hyperspectral Imaging: Acquisition Principles and ExamplesImages and spectra are recorded in a step and stare process, using camera rotation or translation relative to the scene, where the incremental change in scene position is related to the filter linear variation along the spectral axis. This is illustrated in Fig. 12 for a rotating camera. Fig. 12The scene is recorded at different rotational angles, here illustrated with five angles. The combined information from the step and stare images are combined and forming the spectral data cube of the scene. 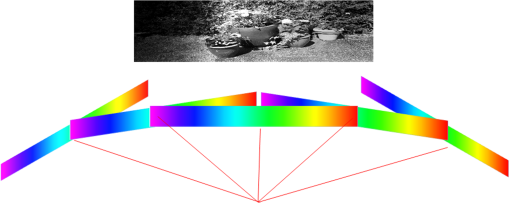 The spectral content of a scene is obtained using a step and stare technique, where the images are recorded one by one while rotating the camera or translating the camera between the frames. In each frame, the pixels are sampled at their uniquely filtered wavelength. There are, therefore, as many spectral points as there are pixels. For each frame during scanning, the scene will be slightly shifted with a new set of spectral samples associated with each pixel position. For number of shifted frames, each scene element will have been sampled at different wavelengths, i.e., the number of effective spectral channels equals the number of frames. To create a hypercube with a common preset spectral axis, the spectral vector is then interpolated to this axis for each image pixel. The finer spectral resolution and, therefore, the maximum number of independent spectral bands are governed by the inherent spectral bandwidth of the LVF and the density of registrations. The number of independent spectral bands is 40 for this filter, but due to the denser sampling needed at shorter wavelength, are needed to obtain full spectral resolution. This can be compared to a conventional push-broom system that, in this case, would require with an array of . In many applications, the spectral slope variation is rather slow and the spectrum can be sampled quite sparsely.23 For an image size of pixels, the total dataset is data-points, which is a rather manageable size for large FPAs as well. Furthermore, the set of frames has to be accurately registered to each other to obtain a hyperspectral, high spatial resolution data cube with a common spectral axis. For a rotating camera, the reconstructing process is relatively simple. For a moving platform causing changes in camera positions relative to the scene topography, the registration process involves the reconstruction of terrain geometry and therefore becomes quite complex. The sensor signal is proportional to the illumination at the specific wavelength, the filter bandwidth, and the quantum efficiency at that wavelength, assuming other parameters as constant. Both the quantum efficiency and the natural illumination decrease in the near-infrared compared to the visible spectral region. The increasing bandwidth is, therefore, beneficial from a signal-to-noise point of view provided the spectral resolution is acceptable for the purpose. The signal will similarly decrease in the blue spectral region due the decreasing bandwidth, decreasing quantum efficiency, and decreasing natural illumination. This consequently causes a decrease in the signal-to-noise ratio in the short end of the spectrum. An example of a scene obtained by the step and stare procedure is shown in Fig. 13, here shown in false color representation. The different images were registered to each other using common scene features,24 which were found accurate enough not to degrade the spatial resolution of the hyperspectral image. From this set of images, a hypercube is created where the spectral properties of the scene can be reconstructed as each point in the scene now contains spectral information. An example of spectra for points on the brick wall and grass field is shown in Fig. 14. The brick wall spectrum can be compared to the spectrum obtained from a wall of a different type of building in Fig. 11. Fig. 14Two spectra were selected from the hyperspectral data cube obtained from the large scene in Fig. 13. (a) A brick wall spectrum is shown in red. The dashed curve is the corresponding reference spectrum obtained from the ASTER database. (b) The green curve is grass spectrum from the field in the foreground. The lower dashed green and upper dashed orange curves are the corresponding reference spectra of green and dry grass obtained from the ASTER database. It can be seen that vegetation is not well developed early in the spring. 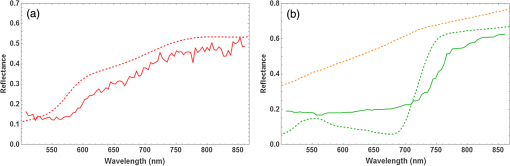 Using the brick wall spectrum as a template for detection, the surface material of the building can be extracted. This is shown in Fig. 15, in which a small section of the building is shown to demonstrate the high spatial resolution and the accuracy in separating only the bricks. Spectral angle mapping (SAM) was used to do the material segmentation. 7.DiscussionThe results so far indicate that the use of LVFs in hyperspectral imaging can be quite effective. Stray light contributions have been modeled and the filter design has proven to be useful with respect to the radiation scattered between the filter and the FPA. The stray light level is shown to be below 10%. Spectral resolution is close to the specification for -numbers larger than . Smaller -numbers will be allowed for by placing the filter closer to the FPA. The camera was also demonstrated as a field spectrometer. The advantage of using an imaging spectrometer is that textures can be separated into several member states. Spectral dependence of the spatial resolution can also be analyzed. Outliers can also be identified. Hyperspectral data cubes can be obtained by either translating the sensor with respect to the scene or by rotating the camera with respect to the scene. Here, only results from rotating the camera are shown. High spatial and spectral quality is demonstrated by means of accurate registrations of the image sequence. The use of the spectral information is exemplified by extracting the brick wall using simple SAM processing. Future activities will focus on the development of software for 3-D hyperspectral scene data extraction obtained from moving platforms.25 Using a moving platform, the scene is simultaneously recorded from different viewpoints and sampled at different wavelengths. In this way, the 3-D scene can be constructed and the spectrum of the scene elements can be determined. For most terrain points, the spectrum will be sampled at different angles, allowing some estimate of the bidirectional reflectance distribution function (BRDF).26 Both the spectral coverage and the 3-D resolution can be improved by using several cameras positioned at different angles. This is more attractive since the cost of each unit has the potential to be very low. However, in many applications, one camera will be adequate. ReferencesI. Renhorn et al.,
“Hyperspectral reconnaissance in urban environment,”
Proc. SPIE, 8704 87040L
(2013). http://dx.doi.org/10.1117/12.2019348 PSISDG 0277-786X Google Scholar
T. Skauli et al.,
“Compact camera for multispectral and conventional imaging based on patterned filters,”
Appl. Opt., 53
(13), C64
–C71
(2014). http://dx.doi.org/10.1364/AO.53.000C64 APOPAI 0003-6935 Google Scholar
J. Loesel and D. Laubier,
“Study of accessible performances of a spectro imager using a wedge filter,”
Proc. SPIE, 7100 710013
(2008). http://dx.doi.org/10.1117/12.796966 PSISDG 0277-786X Google Scholar
N. Tack et al.,
“A compact high-speed and low-cost hyperspectral imager,”
Proc. SPIE, 8266 82660Q
(2012). http://dx.doi.org/10.1117/12.908172 PSISDG 0277-786X Google Scholar
B. Delauré et al.,
“The geospectral camera: a compact and geometrically precise hyperspectral and high spatial resolution imager,”
in Int. Archives of the Photogrammetry, Remote Sensing and Spatial Information Sciences, Volume XL-1/W1, ISPRS Hannover Workshop 2013,
(2013). Google Scholar
D. B. Cavanaugh et al.,
“VNIR hypersensor camera system,”
Proc. SPIE, 7457 745700
(2009). http://dx.doi.org/10.1117/12.833539 PSISDG 0277-786X Google Scholar
H. Saari et al.,
“Novel hyperspectral imager for lightweight UAVs,”
Proc. SPIE, 7668 766805
(2010). http://dx.doi.org/10.1117/12.850091 PSISDG 0277-786X Google Scholar
A. Lucieer et al.,
“HyperUAS—imaging spectroscopy from a multirotor unmanned aircraft system,”
J. Field Rob., 31
(4), 571
–590
(2014). http://dx.doi.org/10.1002/rob.2014.31.issue-4 Google Scholar
A. Pola Fossi et al.,
“Miniature and cooled hyperspectral camera for outdoor surveillance applications in the mid-infrared,”
Opt. Lett., 41 1901
(2016). http://dx.doi.org/10.1364/OL.41.001901 OPLEDP 0146-9592 Google Scholar
“Micro-hyperspec airborne sensors,”
(2016) http://www.headwallphotonics.com/spectral-imaging/hyperspectral/micro-hyperspec May ). 2016). Google Scholar
“AisaKESTREL,”
(2016) http://www.specim.fi/specim-introduces-hyperspectral-sensor-range-for-uavs May ). 2016). Google Scholar
M. T. Eismann, Hyperspectral Remote Sensing, SPIE Press, Bellingham, Washington
(2012). Google Scholar
Y. Gu and M. Anderson,
“Geometric processing of hyperspectral image data acquired by VIFIS on board light aircraft,”
Int. J. Remote Sens., 24 4681
–4698
(2003). http://dx.doi.org/10.1080/0143116031000084305 IJSEDK 0143-1161 Google Scholar
J. W. Jeter and K. R. Blasius,
“Wedge spectrometer concepts for space IR remote sensing,”
Proc. SPIE, 3756 211
(1999). http://dx.doi.org/10.1117/12.366375 PSISDG 0277-786X Google Scholar
M. Dami et al.,
“Ultra compact spectrometer using linear variable filters,”
in Int. Conf. on Optics (ICSO ‘10),
(2010). Google Scholar
J. Loesel and D. Laubier,
“Study of accessible performances of a spectro imager using a wedge filter,”
Proc. SPIE, 7100 710013
(2008). http://dx.doi.org/10.1117/12.796966 PSISDG 0277-786X Google Scholar
Delta Optical Thin Film,
(2016) http://www.deltaopticalthinfilm.com May ). 2016). Google Scholar
J. L. Rienstra,
“Transformation of filter transmission data for f-number and chief ray angle,”
Proc. SPIE, 3377 267
–275
(1998). http://dx.doi.org/10.1117/12.319380 PSISDG 0277-786X Google Scholar
K. D. Möller, Optics, University Science Books, Mill Valley, California
(1988). Google Scholar
A. M. Baldridge et al.,
“The ASTER spectral library version 2.0,”
Remote Sens. Environ., 113 711
–715
(2009). http://dx.doi.org/10.1016/j.rse.2008.11.007 RSEEA7 0034-4257 Google Scholar
J. Theiler and K. Glocer,
“Sparse linear filters for detection and classification in hyperspectral imagery,”
Proc. SPIE, 6233 62330H
(2006). http://dx.doi.org/10.1117/12.665994 PSISDG 0277-786X Google Scholar
C. Liu and P. Chen,
“Automatic extraction of ground control regions and orthorectification of remote sensing imagery,”
Opt. Express, 17
(10), 7970
–7984
(2009). http://dx.doi.org/10.1364/OE.17.007970 OPEXFF 1094-4087 Google Scholar
“Software is under development by Glana sensors AB,”
(2016) http://www.glanasensors.se May ). 2016). Google Scholar
I. Renhorn et al.,
“Four-parameter model for polarization-resolved rough-surface BRDF,”
Opt. Express, 19
(2), 1027
–1036
(2011). http://dx.doi.org/10.1364/OE.19.001027 OPEXFF 1094-4087 Google Scholar
BiographyIngmar G. E. Renhorn was a staff scientist at the Swedish Defense Research Agency (FOI), Linköping, Sweden, from 1981 to 2014. In 1994, he was appointed as a director of research at the Department of IR Systems of FOI. He has been working as a consultant from 2014 to present. Research topics include hyperspectral imaging systems, optical turbulence and aerosol profiling, signature measurement, and sensor systems with applications in reconnaissance, infrared search and track, target acquisition, and optical warning. He is a SPIE fellow and a member of OSA. David Bergström has been a senior scientist at FOI since 2009. Research topics include hyperspectral imaging, polarimetric imaging, and night vision with applications in reconnaissance, surveillance, and target acquisition. He is a member of SPIE. Julia Hedborg has been a research engineer at FOI since 2012, working with EO/IR sensors and signatures. Dietmar Letalick has been employed at the Swedish Defense Research Agency (FOI), Linköping, Sweden, since 1981. He is currently a deputy research director and a group leader for the IR Systems Group. His research interests include optical sensor systems for reconnaissance and target detection, with applications in detection of mines and improvised explosive devices. He is a member of SPIE. |