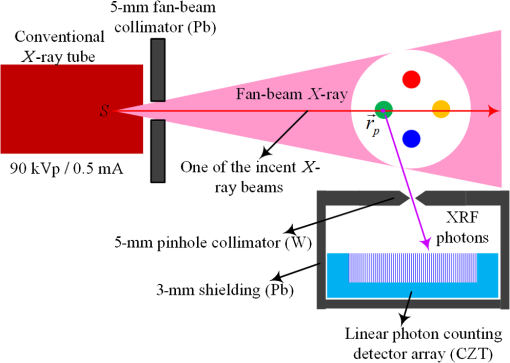
|
|
1.IntroductionX-ray computed tomography (CT) is important for various applications, such as medical diagnosis, industrial nondestructive testing, and security inspection. However, traditional x-ray CT image values provide information only on the linear attenuation coefficients weighted by the spectrum of the incident x-ray beam and cannot accurately identify tumors and constituents. Moreover, this drawback persists in other advanced imaging modes, including molecular imaging with dynamic contrast-enhanced CT.1 As a state-of-the-art technique, spectral CT with multienergy-bin photon-counting detectors enables K-edge imaging. This method uses the K-absorption edge discontinuity of the attenuation coefficients of high-atomic-number elements, such as gadolinium and gold, whose K-edges lie within 50.2 and 80.7 keV, respectively. These K-edge features of contrast agents can be reconstructed and extracted for material-specific quantitative evaluation using data above and below the K-edge energy.2 K-edge imaging aided by gold nanoparticles (NPs) has been used to detect plaque inflammation degree in coronary artery diseases.3 However, the sensitivity of K-edge imaging depends on the scanned object size and its material composition due to beam hardening.4 Different from spectral CT or K-edge imaging, x-ray fluorescence computed tomography (XFCT) detects the characteristic photons from a material excited by initial x-rays. XFCT is a quantitative imaging modality that reconstructs the two-dimensional or three-dimensional distribution of nonradioactive high-atomic-number NPs within a specimen, such as gold, gadolinium, and iodine.5–7 Unlike that in K-edge CT images, the NP contrast in XFCT images is completely independent from the type of surrounding tissue.8 Therefore, XFCT outperforms K-edge CT in imaging contrast agents at low concentrations. Bazalova et al.8 and Feng et al.9 proved that the contrast-to-noise ratio (CNR) of XFCT images is higher than that of transmission K-edge CT images for contrast concentrations below 0.4%. Moreover, XFCT imaging provides more depth localization than fluorescence molecular tomography,10,11 bioluminescence tomography,12 and x-ray luminescence CT with near-IR-emitting nanophosphor.13,14 This advantage is important for preclinical and potential clinical applications. Therefore, with the development of x-ray-excitable NPs, XFCT is a promising modality for molecular imaging in fundamental studies, drug development, and clinical experiments. Early XFCT is performed on high-intensity monochromatic synchrotron radiation sources with large facilities.15–20 The pencil beam/single collimated beam from polychromatic x-ray tubes21–27 is then used to improve the feasibility of using XFCT; however, this technique requires a long scanning time, e.g., 279 min28 and 180 h.29 One important reason for the low efficiency is that using a pencil beam setup requires the beam source to be shifted point by point while measuring a single slice of projection data. Similar processes of shifting on detectors are also required for a fan-beam setup with a single pixel detector.30 Jones and Cho31 demonstrated the simulation results of XFCT using a polychromatic cone-beam source with detector arrays and indicated that the total scanning time can be significantly reduced. Cong et al.32 proposed a fan-beam XFCT setup with detector arrays and evaluated its feasibility through simulation. Apart from the shifting, these XFCT setups rely on spectrum scanning to obtain the spectral information required by Compton scatter compensation. For photon-counting detectors, spectrum scanning generates an enormous waste of x-ray dose, which aggravates the problem. In this paper, we report the first experimental results (to the best of our knowledge) obtained using a full-field fan-beam XFCT consisting of a conventional low-intensity x-ray tube, a multibin photon-counting detector array, and a tungsten pinhole collimator. 2.Methods and Experimental SetupAs shown in Fig. 1, the XFCT process has three steps.33 (1) The incident x-ray photons from the x-ray tube arrives at any position , which can be expressed as where means the x-ray path from the x-ray source to and is the incident photon counts at energy .(2) X-ray fluorescence (XRF) photons are emitted isotropically from position while incident x-ray photons interact with contrast agents. Its intensity can be expressed as where is the photoelectric mass absorption coefficient of the contrast agent, is the yield of fluorescence x-rays, which can be approximated as a constant, and is the concentration of contrast agent at represented as a weight percent.(3) At last, some XRF photons emitted from position travel through the object and are recorded by photon-counting detectors where means the XRF path starting from to the detector and passing the pin-hole collimator. is the linear attenuation coefficient of XRF photons. Ang is the solid angle range covered by the detector from . denotes the line on which the emitted XRF is collected by the detector.Then, the intensity map of generated XRF photons can be reconstructed using the iterative maximum-likelihood expectation maximization (ML-EM) algorithm as34 where is the coefficient of the imaging matrix that can be calculated from the XFCT geometry, denotes the ’th XRF photon beam, and denotes the ’th pixel of the reconstructed map, . At last, the distributions and concentration of the contrast agents, , can be calculated using Eqs. (1) and (2) and .Figure 2(a) shows a photograph of our XFCT imaging setup. A low-brilliance x-ray beam (90 kV, 0.5 mA) was generated using a conventional Hamamatsu L12161-07 x-ray tube. The x-ray beam was collimated using lead plates in two directions to produce a fan beam. To reduce the total dose and scattering photons, a 0.3-mm Cu sheet was placed at the x-ray tube exit. A home-made polymethyl methacrylate (PMMA) phantom was set to rotate in precise steps using a computer-controlled motion stage, whereas the x-ray tube and the detector were stationary. The third-generation CT scanning mode was used with a rotational step of 1 deg over a full scan. At each angle view, XFCT data emitted from the whole phantom illuminated using the full-field fan-beam were collected by a linear photon-counting detector array (eV3500, eV PRODUCTS, Saxonburg, Pennsylvania). As shown in Fig. 2(b), a 5-mm tungsten pinhole collimator was placed before the detector. This x-ray detector used a 3-mm CdZnTe semiconductor, 256 pixels at a 0.5-mm pixel pitch, and five adjustable energy thresholds.33 The detector was placed at a 90-deg angle to the incident x-ray beam to minimize the number of scattering photons entering the detector. Furthermore, a 3-mm lead cover was used to shield the whole detector box from x-rays coming from outside the field of view. Moreover, the same x-ray detector was repositioned behind the phantom along the beam direction to provide transmission spectral CT measurements and correct the attenuation. A PMMA phantom containing water and gadolinium solution insertions was prepared, as shown in Fig. 2(c). The insertions consisted of 1%, 2%, 3%, and 4% (weight/volume) gadolinium solutions. The phantom dimension was 35 mm in diameter. 3.ResultsFigure 3 shows the sinograms (projection data, ) of the XFCT experiment. Per rotation, 360 projections were acquired at a frame duration of 5 s. This scenario resulted in a total measurement time of 30 min per slice and a dose equivalent of 900 mAs. The energy thresholds were set at 35, 40, 45, 50, 70, and 90 keV. The peak of gadolinium was located at 42.74 keV; hence, the data within the 40- to 45-keV energy bin were used for XFCT. Figure 3(a) shows the raw XFCT data. Although the detector was energy calibrated,35,36 it had obvious streak artifacts because of the inconsistencies among the different detector elements. Figure 3(b) shows the gain correction results based on Fig. 3(a), wherein most of the streak artifacts were removed. However, the background was strong due to the scattered photons. The state-of-the-art XFCT systems rely on spectrum analysis to distinguish a signal from scattering; single-pixel spectrometers serve this function but generate an enormous waste of acquisition time and x-ray dose. Inspired by a method designed for single-photon emission computed tomography systems,37 we propose to compensate for the Compton scattering based on energy bins rather than spectra. Considering that the scattering angle of each pixel is known, we can calculate the Compton scattering cross section based on the Klein–Nishina formula. With the incident tube spectrum obtained by simulation, we can determine the energy distribution of scattering photons. Based on this distribution, we can then estimate the scattering at 40 to 45 keV, which is mixed with the 42.74-keV XRF signal, by direct measurement of the scattering on nearby bins of 35 to 40 and 45 to 50 keV because XRF signals are theoretically absent. The scattering on the target energy bin can be calculated as where , , and denote the theoretical relative numbers of scattered photons, which are calculated by the energy distribution of scattering photons mentioned above. Figure 3(c) shows the scattering correction results based on Fig. 3(b), wherein the background was effectively reduced.Fig. 3Projection data (sinograms) of the XFCT: (a) raw data, (b) gain correction data based on (a), and (c) scattering correction data based on (b). 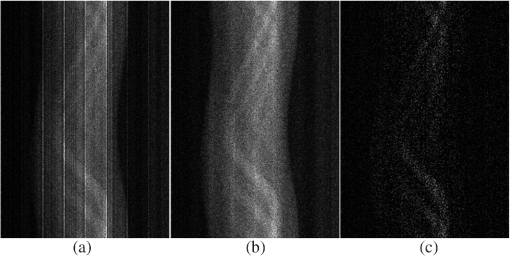 Figure 4 shows the XFCT reconstruction images using the ML-EM algorithm. Figure 4(a) shows the image reconstructed from the raw data of Fig. 3(b). The image shows an obvious background beside the gadolinium solution regions caused by the scattered photons. Figure 4(b) shows the image reconstructed from the scattering correction data of Fig. 3(c) where the strong background in Fig. 4(a) was effectively removed. In the 40- to 45-keV energy bin, there are averagely 18.41 photons per pixel per angle in the range of the phantom, while after the scattering correction the number drops to 3.47. Notably, XRF photons are also attenuated by the object before entering the detector. Therefore, attenuation correction should also be considered.38 The attenuation map can be reconstructed using additional or simultaneous transmission spectral CT scan. Figure 4(c) shows the attenuation correction result based on Fig. 4(b) using the attenuation map reconstructed from the transmission spectral CT data in the 40- to 45-keV energy bin. With attenuation correction, the brightness of Fig. 4(c) is much higher than that of Fig. 4(b). Fig. 4(a) and (b) The ML-EM reconstruction results from the XFCT data of Figs. 3(b) and 3(c), respectively. (c) The attenuation correction result based on (b). The red circles indicate the sampling points for Table 1.  Table 1Average gadolinium concentrations calculated from the results of Fig. 4.
To quantify the XFCT reconstructions in Fig. 4, we calculated the average gadolinium concentration values in the regions-of-interest (ROI) marked by the red circles. The results are shown in Table 1. In the second row, the values in Fig. 4(a) are larger than the truth because the XFCT data in Fig. 4(a) contain many scattered photons that increased the calculated concentrations. After the scattering correction, the values in the third row were reduced and even smaller than the truth. As shown in the fourth row, attenuation correction can improve the reconstructed concentrations to correspond with the true values. For comparison, spectral CT imaging was performed using the same hardware and scanning parameters, e.g., kVp and mAs. The difference was that the detector array was placed against the central x-ray beam, and the energy thresholds were changed to 40, 45, 50, 55, 73, and 90 keV because the K-edge of gadolinium was located at 50.229 keV. Figure 5(a) shows the decomposition results of gadolinium from the spectral CT reconstruction. Material decomposition magnified the inconsistencies among different detector elements and resulted in strong ring artifacts. Fig. 5Comparison between spectral CT and XFCT. (a) Decomposition results of gadolinium from the spectral CT reconstruction. (b) XFCT reconstruction same with Fig. 4(c). The red circles indicate the sampling points of signal, whereas the blue ones indicate the sampling points of noise for the CNR as shown in Table 2.  Table 2CNR comparisons between Figs. 5(a) and 5(b). The images in Fig. 5 were evaluated as CNR by calculating the ratio of the difference between the mean value of each ROI (red circles) and background (PMMA, blue circles) and standard deviation of the background. As shown in Table 2, the CNR of the reconstructed XFCT image is higher than that of the corresponding spectral CT image due to its strong background. Moreover, XFCT may have a higher sensitivity than spectral CT (including K-edge CT) in molecular contrast imaging. Therefore, XFCT could be superior to spectral CT in the presence of low concentrations of contrast agents. 4.ConclusionA study of full-field fan-beam XFCT using conventional low-intensity x-ray tube and energy-sensitive photon-counting detectors is presented. Unlike other pencil beam studies, a fan beam produced using a polychromatic x-ray tube was used to stimulate emissions of XRF photons that were collected by passing through a tungsten pinhole collimator. Thus, a whole XFCT scan can be completed within 30 min using third-generation CT geometry, which is faster than other XFCT devices that use a pencil beam with a first-generation CT geometry. Experimental results showed that scattering and attenuation correction are indispensable for highly accurate XFCT reconstruction. Moreover, the CNR of the XFCT image is higher than that of the corresponding spectral or K-edge CT image because a strong background exists adjacent to the contrast agent regions in spectral or K-edge CT images. This full-field XFCT has high sensitivity in molecular contrast imaging and is a promising modality for biomedical imaging of molecular probes. A multipinhole collimator and large detector arrays may be used in future XFCT experiments to improve the efficiency of using XRF photons. AcknowledgmentsThis work was partially supported by National Natural Science Foundation of China, Award Nos: 61571256, 81427803, and 11525521; and Beijing Municipal Science and Technology Commission, Award No. Z151100003915079. ReferencesK. A. Miles,
“Molecular imaging with dynamic contrast-enhanced computed tomography,”
Clin. Radiol., 65 549
–556
(2010). http://dx.doi.org/10.1016/j.crad.2010.04.007 Google Scholar
E. Roessl and R. Proksa,
“K-edge imaging in x-ray computed tomography using multi-bin photon counting detectors,”
Phys. Med. Biol., 52
(15), 4679
–4696
(2007). http://dx.doi.org/10.1088/0031-9155/52/15/020 PHMBA7 0031-9155 Google Scholar
Y. Alivov et al.,
“Optimization of K-edge imaging for vulnerable plaques using gold nanoparticles and energy resolved photon counting detectors: a simulation study,”
Phys. Med. Biol., 59 135
–152
(2014). http://dx.doi.org/10.1088/0031-9155/59/1/135 PHMBA7 0031-9155 Google Scholar
E. Roessl et al.,
“Sensitivity of photon-counting based K-edge imaging in x-ray computed tomography,”
IEEE Trans. Med. Imaging, 30
(9), 1678
–1690
(2011). http://dx.doi.org/10.1109/TMI.2011.2142188 ITMID4 0278-0062 Google Scholar
G. F. Rust and J. Weigelt,
“X-ray fluorescent computer tomography with synchrotron radiation,”
IEEE Trans. Nucl. Sci., 45
(1), 75
–88
(1998). http://dx.doi.org/10.1109/23.659557 IETNAE 0018-9499 Google Scholar
G. Pratx et al.,
“Tomographic molecular imaging of x-ray-excitable nanoparticles,”
Opt. Lett., 35
(20), 3345
–3347
(2010). http://dx.doi.org/10.1364/OL.35.003345 OPLEDP 0146-9592 Google Scholar
S. K. Cheong et al.,
“X-ray fluorescence computed tomography (XFCT) imaging of gold nanoparticle-loaded objects using 110 kVp x-rays,”
Phys. Med. Biol., 55
(3), 647
–662
(2010). http://dx.doi.org/10.1088/0031-9155/55/3/007 PHMBA7 0031-9155 Google Scholar
M. Bazalova et al.,
“Investigation of x-ray fluorescence computed tomography (XFCT) and K-edge imaging,”
IEEE Trans. Med. Imaging, 31 1620
–1627
(2012). http://dx.doi.org/10.1109/TMI.2012.2201165 ITMID4 0278-0062 Google Scholar
P. Feng et al.,
“Analytic comparison between x-ray fluorescence CT and K-edge CT,”
IEEE Trans. Biomed. Eng., 61
(3), 975
–985
(2014). http://dx.doi.org/10.1109/TBME.2013.2294677 IEBEAX 0018-9294 Google Scholar
V. Ntziachristos et al.,
“Looking and listening to light: the evolution of whole-body photonic imaging,”
Nat. Biotechnol., 23 313
–320
(2005). http://dx.doi.org/10.1038/nbt1074 NABIF9 1087-0156 Google Scholar
X. Liu et al.,
“Principal component analysis of dynamic fluorescence diffuse optical tomography images,”
Opt. Express, 18
(6), 6300
–6314
(2010). http://dx.doi.org/10.1364/OE.18.006300 OPEXFF 1094-4087 Google Scholar
G. Wang et al.,
“In vivo mouse studies with bioluminescence tomography,”
Opt. Express, 14
(17), 7801
–7809
(2006). http://dx.doi.org/10.1364/OE.14.007801 OPEXFF 1094-4087 Google Scholar
X. Liu, Q. M. Liao and H. K. Wang,
“In vivo x-ray luminescence tomographic imaging with single-view data,”
Opt. Lett., 38
(22), 4530
–4533
(2013). http://dx.doi.org/10.1364/OL.38.004530 OPLEDP 0146-9592 Google Scholar
C. Li et al.,
“X-ray luminescence optical tomography imaging: experimental studies,”
Opt. Lett., 38
(13), 2339
–2341
(2013). http://dx.doi.org/10.1364/OL.38.002339 OPLEDP 0146-9592 Google Scholar
Q. Huo et al.,
“Sheet-beam geometry for in vivo fluorescent x-ray computed tomography: proof-of-concept experiment in molecular imaging,”
Opt. Lett., 33
(21), 2494
–2496
(2008). http://dx.doi.org/10.1364/OL.33.002494 OPLEDP 0146-9592 Google Scholar
B. Deng et al.,
“3D elemental sensitive imaging by full-field XFCT,”
Analyst, 140
(10), 3521
–3525
(2015). http://dx.doi.org/10.1039/C4AN02401J ANLYAG 0365-4885 Google Scholar
G. Fu et al.,
“Experimental demonstration of novel imaging geometries for x-ray fluorescence computed tomography,”
Med. Phys., 40
(6), 061903
(2013). http://dx.doi.org/10.1118/1.4801907 MPHYA6 0094-2405 Google Scholar
T. Takeda et al.,
“Fluorescent x-ray computed tomography to visualize specific material distribution,”
Proc. SPIE, 3149 160
(1997). http://dx.doi.org/10.1117/12.279355 OSCADN Google Scholar
T. Takeda et al.,
“Human thyroid specimen imaging by fluorescent x-ray computed tomography with synchrotron radiation,”
Proc. SPIE, 3772 258
(1999). http://dx.doi.org/10.1117/12.363728 Google Scholar
T. Takeda et al.,
“X-ray fluorescent CT imaging of cerebral uptake of stable-iodine perfusion agent iodoamphetamine analog IMP in mice,”
J. Synchrotron Radiat., 16
(1), 57
–62
(2009). http://dx.doi.org/10.1107/S0909049508031853 JSYRES 0909-0495 Google Scholar
G. Pratx et al.,
“X-ray luminescence computed tomography via selective excitation: a feasibility study,”
IEEE Trans. Med. Imaging, 29
(12), 1992
–1999
(2010). http://dx.doi.org/10.1109/TMI.2010.2055883 ITMID4 0278-0062 Google Scholar
N. Manohar, B. L. Jones and S. H. Cho,
“Improving x-ray fluorescence signal for benchtop polychromatic cone-beam x-ray fluorescence computed tomography by incident x-ray spectrum optimization: a Monte Carlo study,”
Med. Phys., 41
(10), 101906
(2014). http://dx.doi.org/10.1118/1.4895004 MPHYA6 0094-2405 Google Scholar
H. M. Hertz et al.,
“Laboratory x-ray fluorescence tomography for high-resolution nanoparticle bio-imaging,”
Opt. Lett., 39
(9), 2790
–2793
(2014). http://dx.doi.org/10.1364/OL.39.002790 OPLEDP 0146-9592 Google Scholar
P. L. Riviere et al.,
“Penalized-likelihood image reconstruction for x-ray fluorescence computed tomography,”
Opt. Eng., 45
(7), 077005
(2006). http://dx.doi.org/10.1117/1.2227273 Google Scholar
Y. Kuang et al.,
“Development of XFCT imaging strategy for monitoring the spatial distribution of platinum-based chemodrugs: instrumentation and phantom validation,”
Med. Phys., 40
(3), 030701
(2013). http://dx.doi.org/10.1118/1.4789917 MPHYA6 0094-2405 Google Scholar
M. Bazalova et al.,
“L-shell x-ray fluorescence computed tomography (XFCT) imaging of Cisplatin,”
Phys. Med. Biol., 59
(1), 219
–232
(2014). http://dx.doi.org/10.1088/0031-9155/59/1/219 PHMBA7 0031-9155 Google Scholar
N. Manohar, F. J. Reynoso and S. H. Cho,
“Experimental demonstration of direct L-shell x-ray fluorescence imaging of gold nanoparticles using a benchtop x-ray source,”
Med. Phys., 40
(8), 080702
(2013). http://dx.doi.org/10.1118/1.4816297 MPHYA6 0094-2405 Google Scholar
Y. Kuang et al.,
“First demonstration of multiplexed x-ray fluorescence computed tomography (XFCT) imaging,”
IEEE Trans. Med. Imaging, 32
(2), 262
–267
(2013). http://dx.doi.org/10.1109/TMI.2012.2223709 ITMID4 0278-0062 Google Scholar
A. Groll et al.,
“Element mapping in organic samples utilizing a benchtop x-ray fluorescence emission tomography (XFET) system,”
IEEE Trans. Nucl. Sci., 62
(5), 2310
–2317
(2015). http://dx.doi.org/10.1109/TNS.2015.2465380 IETNAE 0018-9499 Google Scholar
B. L. Jones et al.,
“Experimental demonstration of benchtop x-ray fluorescence computed tomography (XFCT) of gold nanoparticle-loaded objects using lead-and tin-filtered polychromatic cone-beams,”
Phys. Med. Biol., 57
(23), N457
(2012). http://dx.doi.org/10.1088/0031-9155/57/23/N457 PHMBA7 0031-9155 Google Scholar
B. L. Jones and S. H. Cho,
“The feasibility of polychromatic cone-beam x-ray fluorescence computed tomography (XFCT) imaging of gold nanoparticle-loaded objects: a Monte Carlo study,”
Phys. Med. Biol., 56
(12), 3719
–3730
(2011). http://dx.doi.org/10.1088/0031-9155/56/12/017 PHMBA7 0031-9155 Google Scholar
W. X. Cong et al.,
“X-ray fluorescence tomographic system design and image reconstruction,”
J. X-Ray Sci. Technol., 21 1
–8
(2013). http://dx.doi.org/10.3233/XST-130362 JXSTE5 0895-3996 Google Scholar
L. Li et al.,
“Simultaneous x-ray fluorescence and K-edge CT imaging with photon-counting detectors,”
Proc. SPIE, 9967 99670F
(2016). http://dx.doi.org/10.1117/12.2238528 PSISDG 0277-786X Google Scholar
L. A. Shepp and Y. Vardi,
“Maximum likelihood reconstruction for emission tomography,”
IEEE Trans. Med. Imaging, 1
(2), 113
–122
(1982). http://dx.doi.org/10.1109/TMI.1982.4307558 ITMID4 0278-0062 Google Scholar
R. Z. Li, L. Li and Z. Q. Chen,
“Spectrum reconstruction method based on the detector response model calibrated by x-ray fluorescence,”
Phys. Med. Biol., 62 1032
–1045
(2017). http://dx.doi.org/10.1088/1361-6560/62/3/1032 PHMBA7 0031-9155 Google Scholar
R. Z. Li, L. Li and Z. Q. Chen,
“Feasible energy calibration for multi-threshold photon-counting detectors based on reconstructed XRF spectra,”
IEEE Trans. Radiat. Plasma Med. Sci., 1
(2), 109
–120
(2017). http://dx.doi.org/10.1109/TNS.2016.2645721 IETNAE 0018-9499 Google Scholar
T. Ichihara et al.,
“Compton scatter compensation using the triple-energy window method for single-and dual-isotope SPECT,”
J. Nucl. Med., 34
(12), 2216
–2221
(1993). https://doi.org/http://jnm.snmjournals.org/content/34/12/2216.long Google Scholar
J. P. Hogan, R. A. Gonsalves and A. S. Krieger,
“Fluorescent computer tomography: a model for correction of x-ray absorption,”
IEEE Trans. Nucl. Sci., 38
(6), 1721
–1727
(1991). http://dx.doi.org/10.1109/TNS.1991.574221 IETNAE 0018-9499 Google Scholar
BiographyLiang Li received his PhD from Tsinghua University in Beijing, China, in 2007. Currently, he is an associate professor in the Department of Engineering Physics, Tsinghua University. His research interests center on the mathematical and physical problems of x-ray imaging and its medical, industrial, and other applications. |