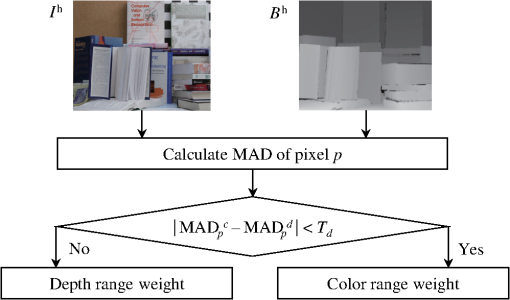
|
|
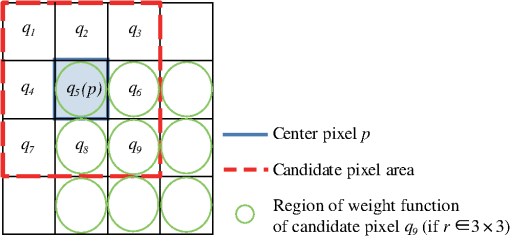
1.IntroductionResolution of a depth image captured by a three-dimensional (3-D) camera for depth sensing is generally lower than its corresponding color image for 3-D video applications. In addition, an advanced 3-D TV system transmits low-resolution depth images to make the best use of a transmission bandwidth. For practical purposes, an efficient depth image upsampling algorithm is necessary to adjust the resolution between depth and color images. There are a number of depth image upsamplers. The bilinear interpolator and bicubic interpolator can be directly used for depth image upsampling. These interpolators generate good results in smooth regions, but make noise looked like the shape of staircase in the edge. To remove the staircase noise, some depth image upsamplers based on weight functions have been introduced.1–3 These studies show positive results for staircase noise, but generate the drawback of texture copy problem caused by a distinct color pattern. In this paper, we propose a depth image upsampling algorithm to overcome these problems, such as staircase noise and texture copy problem. The proposed algorithm suggests an effective weight choice method and a color weight function. 2.Joint Bilateral FilterTo increase the sampling rate of a depth image, Kopf et al.1 have developed a joint bilateral upsampler (JBU) by extending the idea of a joint bilateral filter based on weight functions. Suppose that there are a low-resolution depth image and a high-resolution color image . Let and denote the pixel coordinates in the low-resolution image and the high-resolution image, respectively. is the center of the local neighborhood and is the neighboring pixel location of . The depth value at in an upsampled depth image is calculated by a normalized weighted sum, which is expressed as where and are the spatial and range weighting functions, respectively. The and are modeled by the exponential function as follows: where is a Euclidean distance operator. and are the smoothing parameters of and , respectively.3.Proposed Depth Image UpsamplerTo get an upsampled depth image while keeping the shape of the edge without staircase noise, the previous works1–3 define the color weight function and take advantage of the color information under the assumption that depth and color images have similar characteristics. However, the use of color weight occasionally causes an unexpected depth in smooth areas when a distinct pattern is in the color image. This phenomenon is called texture copy problem. To reduce the texture copy problem, we propose a weight selection algorithm that selectively applies a range weight function for cost calculation: color range weight function or depth range weight function. In addition, we define a color range weight function based on Laplacian distribution to utilize the color information more effectively. Figure 1 shows the overall flow of the proposed upsampler. First, a low-resolution depth image is upsampled by a bicubic interpolation algorithm and the upsampled high-resolution depth image is denoted by . Then, all pixels in the upsampled depth image should be tested by weight selection algorithm whether the pixel belongs to a distinct color pattern or not. Next, the cost values between the center pixel and the surrounding pixels are calculated based on spatial and range weight functions. Finally, when the candidate pixel at has the minimum cost among the nine candidates, the depth value at is replaced by the depth value at . After obtaining the upsampled depth image by the bicubic interpolation algorithm, we perform the weight selection algorithm for all pixels, as shown in Fig. 2. If we detect a distinct color pattern in a color image, we do not use the color image information to avoid the texture copy problem. To detect a distinct color pattern, we compare the mean of absolute difference (MAD) of the color image and that of the depth image. The MAD of the color image at and the MAD of the depth image are denoted as and and calculated as Then we calculate the absolute difference (AD) between and If the predefined difference threshold is bigger than , we can expect that the color texture problem will not happen because there is no big differences between neighboring pixels in the color image. In this case, we use a color range weight function for cost calculation. If is smaller than , we select a depth range weight function to remove the effects of the color image.Figure 3 shows the pixel position for cost calculation and weight function. The cost at with respect to is calculated as where The region weight is a weighted sum of spatial and range weight functions between and its neighbor . To calculate the value of the region weight, we use the result of weight selection algorithm. In the equation below , the spatial weight function and the depth range weight function are modeled as a simplified Gaussian function where and are the smoothing parameters of and , respectively. However, unlike predefined weight functions, a color range weight function is modeled as a simplified Laplacian function to reduce the effect of color information. The Laplacian function is narrower and sharper than the Gaussian function. It is also expressed by an exponential function where is the smoothing parameter of .After calculating each cost of all nine candidates, we find the minimum cost among these nine candidates. Minimum cost pixel is represented as Finally, is replaced with a pixel generating the minimum cost4.Simulation ResultsTo evaluate the performance of the depth image upsampling algorithm, we performed computer simulations on various images having ground truth depth data. To generate input 8-bit low-resolution depth images, each ground truth depth image is downsampled by a factor of 2 and 4. The performance of the proposed algorithm was compared to the JBU,1 joint trilateral upsampler (JTU),2 and fast edge preserving depth upsampler (FEDU)3 in terms of peak signal-to-noise ratio (PSNR) and subjective visual quality. In the simulation, the cost function parameters were set by , , , , , and . Tables 1 and 2 show the results of PSNR comparison. When the upsampling factor is 2, the proposed upsampler has higher PSNRs by as much as about 11.11, 11.3, and 2.54 dB than JBU,1 JTU,2 and FEDU3 on average, respectively. When the upsampling factor is 4, the PSNR gains of the proposed algorithm are 6.57, 4.21, and 2.65 dB higher than JBU,1 JTU,2 and FEDU3 on average, respectively. Table 1PSNR comparison (unit: dB and upsampling factor: 2).
Table 2PSNR comparison (unit: dB and upsampling factor: 4).
As shown in Figs. 4 and 5, the excellence of the proposed algorithm is also demonstrated by a subjective visual quality test. The first image is the color image and the region of interest is marked by a red box. (a), (b), and (c) are the results of JBU, FEDU, and the proposed algorithm, respectively. Sawtooth and art are upsampled by 4 and 2. From the result of JBU in Fig. 4(a), the staircase distortion is observed. FEDU3 reduces the staircase distortion. but there remain blurring artifacts in the sharp edge as shown in Fig. 4(b). However, the proposed algorithm generates a sharp edge without blurring artifacts. In addition, we can see the reduced texture copy problem in Fig. 5(c) compared to the result of JBU in Fig. 5(a). 5.ConclusionA depth image upsampler has been proposed to preserve edge information and reduce the texture copy problem. To achieve the goal, we introduced the weight selection algorithm and the color range weight function based on a Laplacian distribution model. Computer simulations were performed on various test images to show the superiority of the proposed algorithm. The simulation results demonstrate that the proposed scheme has advantages in terms of PSNR and subjective visual quality. As a result, the increased upsampled depth image quality can lead to an improvement in the virtual view synthesis and multiview 3-D videos. AcknowledgmentsThis research was supported by the Basic Science Research Program through the National Research Foundation of Korea funded by the Ministry of Education (No. 2014R1A1A2057662) and research projects of “The Development of Security and Safety Systems based on Ubiquitous Technology for Shipping and Logistics.” ReferencesJ. Kopf et al.,
“Joint bilateral upsampling,”
ACM Trans. Graphics, 26
(3), 1
–6
(2007). http://dx.doi.org/10.1145/1276377 ATGRDF 0730-0301 Google Scholar
Y. Li et al.,
“Depth map super-resolution via iterative joint trilateral upsampling,”
in IEEE Conf. on Visual Communications and Image Processing,
386
–389
(2014). http://dx.doi.org/10.1109/VCIP.2014.7051587 Google Scholar
S. Y. Kim and Y. S. Ho,
“Fast edge-preserving depth image upsampler,”
IEEE Trans. Consum. Electron., 58
(3), 971
–977
(2012). http://dx.doi.org/10.1109/TCE.2012.6311344 ITCEDA 0098-3063 Google Scholar
|