|
|
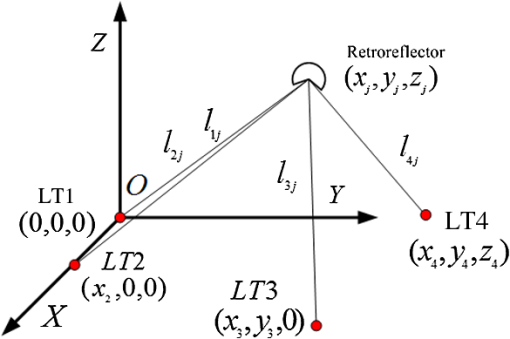
1.IntroductionWith the rapid development of advanced manufacturing and assembly technologies, spatial large-scale coordinate measurement technology plays an increasingly important role in the geometric measurement to support the assembly of large components in the production of aircraft, shipbuilding, and other large machine tools.1 At present, the experimental advanced superconducting tokamak (EAST) is a large superconducting tokamak fusion device, which has complicated structures and highly accurate assembly requirements.2 EAST is divided into the outside and inside of the vacuum chamber by a wall. In the past, the assembly job of the outside key components of the vacuum chamber was accomplished by using a total station and digital level.3–7 However, a total station or digital level cannot measure the components in the vacuum chamber because the light-of-sight would be blocked by the walls. The assembly processes of the inner key components of EAST is normally inspected by the measurement template. The existing measurement method using the template has low accuracy and low-efficiency, which cannot satisfy the assembly accuracy requirement in the reconstruction process of EAST. The precision measurement network is usually established by using high efficiency and high precision instruments. The laser tracker (LT) which has a large measuring range, high precision, high efficiency, etc., is one of the most efficient large scale measuring instruments. It is widely used in measurement jobs of large-scale artifacts. In recent years, a multistation method was proposed based on the highly accurate measuring distance-to-calibration machine tool,8 articulated CMM9,10 or on establish the high precision measuring network.11–13 However, a multistation method also cannot measure the hidden components of a large-scale and complicated structural device. To solve the measurement problem of a large-scale and complicated structural device, which cannot be achieved by a single instrument, Tong et al.14 and Gu et al.15 had proposed an LT combined with an articulated CMM. But they did not evaluate the measurement uncertainty of the measurement system. The measurement uncertainty of the precision measurement network is one of the most important indices used to evaluate its quality based on the multistation method. Estler et al.16 introduced a direct estimate of the uncertainty of the base points only expressed by the residuals of the length. This method, however, does not provide a clear definition of the uncertainty of the measured point itself. To solve this difficulty, an approach17 which calculates the measurement uncertainty of the base point based on multistation is adopted in this paper. According to the characteristics of EAST, an external precision measurement network is established by using the multistation method and the inner network is established based on the best-fit transformation method. Meanwhile, the measurement uncertainties of the external precision measurement network can be analyzed by the method proposed by Zhang. The measurement uncertainties of the overall precision measurement network are evaluated by the Unified Metrology Spatial Network (UMSN) module of spatial analyzer (SA) software. Finally, the inspection tasks of the key components assembly are finished by using the inner precision measurement network to position the articulated CMM. 2.Principles of Precise Measurement Network of EAST2.1.Theoretical Principles of MultistationLT is made up of two angle measurement systems and one highly accurate measurement distance system. The principle of multistation is shown in Fig. 1. Four stations (LT) are located at the world coordinate, and indicates the distances between LT, , and the retroreflector . Equation (1) is established by the distance formula of two points based on the characteristics of the highly accurate measuring distance of LT. The objective, Eq. (2), is established by Eq. (1): whereTo reduce the number of unknown parameters, the origin of LT1 (0, 0, 0) is supposed to be the origin of the world coordinate. LT2 is on the axis. LT3 is located at the plane. LT4 is at the space. Suppose that these unknown parameters are indicated by whose corresponding element is represented by . To solve the above unknown parameters, the calculation method as follows:
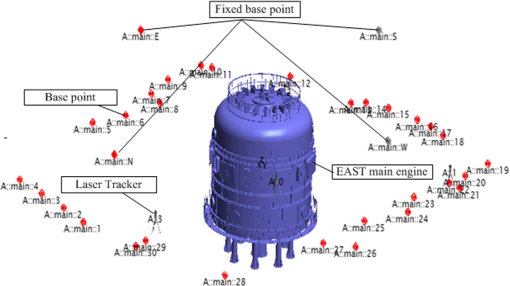
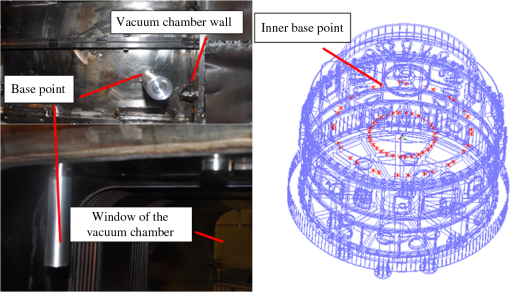
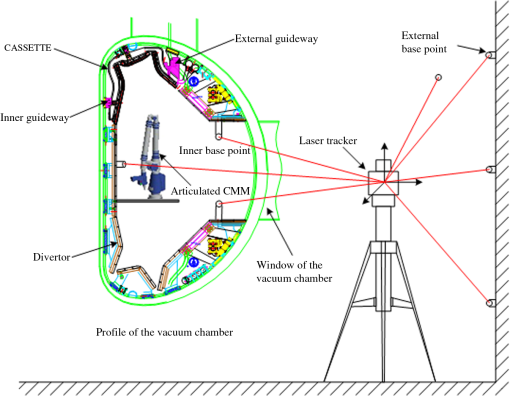
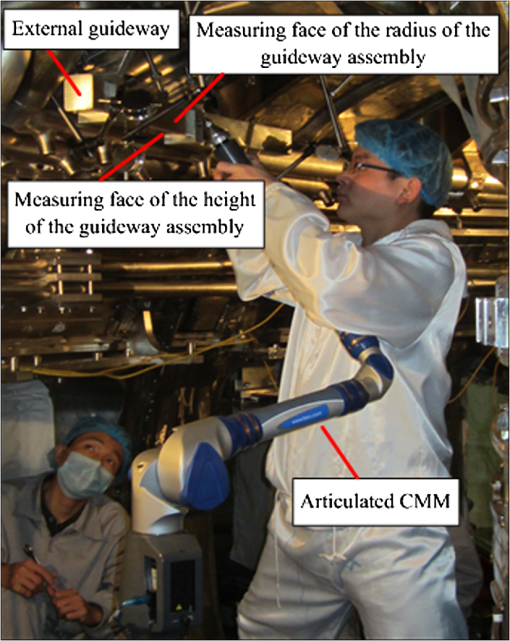
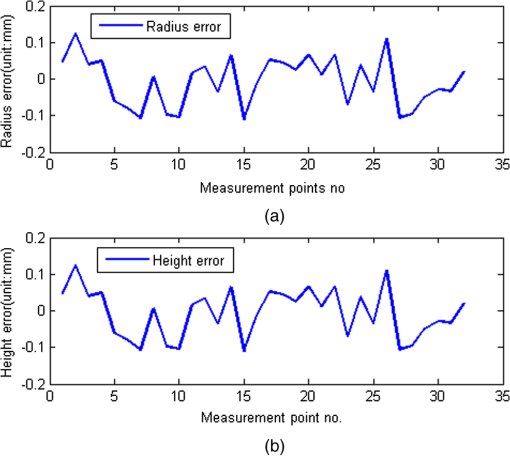
Finally, the vector can be identified by the Gauss-Newton iterative algorithm. 2.2.Measurement Uncertainty Evaluation of the Multistation MethodAccording to the error theory, the error of least squares method of Eq. (1) can be expressed as Eq. (4): where indicates the vector of the measured base point ; is the covariance matrix of ; is the covariance matrix of the distance ; is the standard deviation of the measuring length of LT; and is the Jacobian matrix of Eq. (1).Equation (4) is rewritten as Eq. (5): whereThe three components of the standard deviation of the measured base point are expressed as Eq. (6): The measuring standard deviation of the measured base point is calculated by using Eq. (6): 3.Establishment of Precision Measurement NetworkThe EAST device, is divided into outside and inside the vacuum chamber by its walls, is shown in Fig. 2. Based on the structural characteristics of EAST, a precision measurement network, which consists of the external and inner precision measurement networks, is established to ensure the consistency of the assembled base of all components. 3.1.External Precision Measurement NetworkThe thickness of the walls of the hall is 1.5 m, and the walls of the hall can be used as the fixed base of the base point. First, four fixed base points are placed against each wall for establishing the coordinate system of EAST in the hall. Second, 30 base points are evenly distributed at each wall for facilitating the establishment of an inner precision measurement network through the opening windows of EAST in the reconstruction process. Combined with the distributions of EAST devices in the hall, the external precision measurement network is established by moving LT for four different positions. The distributed positions of the external base points and LTs are shown in Fig. 3. 3.2.Establishment of the Inner Precision Measurement Network and Relocation of Articulated CMMBased on the inner structure of EAST, four base points which are individually fixed at the corresponding vacuum chamber wall and the neck of each window of the vacuum chamber are shown in Fig. 4. These points are evenly fastened at the Vacuum Chamber wall and neck of each window. To accomplish the inspection tasks of the key components of the vacuum chamber, LT, which is installed at the visible window of the vacuum chamber, is located at the world coordinate through measuring the base points of the external precision measuring network and using the best-fit transformation. Likewise, the articulated CMM is relocated in the vacuum chamber through the inner precision measurement network. The establishment of the inner precision measurement network and the relocation of the articulated CMM are shown in Fig. 5. 4.Measurement Uncertainties Analysis of Precision Measurement NetworkUsually, the measured results contain some uncertainty factors because of the influences of the measurement environment, instrument errors, operators, etc. It is known that the measurement uncertainty is viewed as one of the most important indices for evaluating the quality of a precision measurement network. In this paper, the measurement uncertainties of the external precision measurement network are calculated by Eq. (7), and the measurement uncertainties of the overall precision measuring network are analyzed by the USMN module of SA at a confidence probability of 95.44%. The analysis results of the measurement uncertainties of the precision measurement network are shown in Fig. 6. Fig. 6Analysis results of the measurement uncertainties of precision measurement network: (a) external and (b) overall. 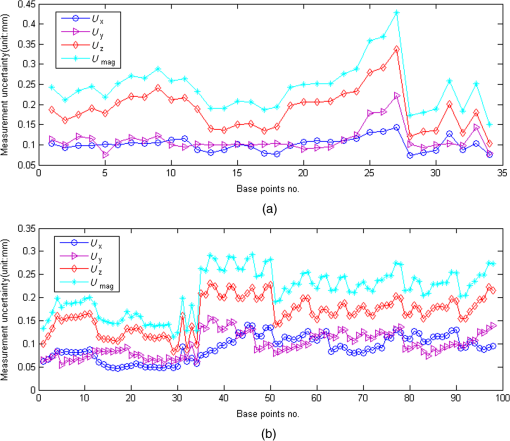 Figure 6 shows that measurement uncertainty of the single point of the precision measurement network is 0.20 mm, where the component is considered as the main factor. The established precision measurement network can satisfy the assembly requirements at a measurement uncertainty lower than 25% of the assembly tolerance. 5.Inspection of the External Guideway Assembly of Vacuum ChamberThe assembly position of the external guideway is shown in Fig. 5 and its assembly requirement is 0.20 mm for both the height and the radius. The inspection process of the external guideway assembly is shown in Fig. 7. The assembly errors of the external guideway inspected by the articulated CMM are shown in Fig. 8. Figure 8 shows that the assembly errors between the measured values and the nominal values are mainly distributed in [](mm). The assembly errors of the external guideway can be satisfied with its assembly requirements. 6.ConclusionsThis paper proposes a precision measurement network for EAST based on multistation and best-fit transformation methods. The measurement uncertainty, which is evaluated by the USMN module of SA, is 0.20 mm at a confidence probability of 95.44%. The established precision measuring network could satisfy the assembly requirement, which is , and the measurement uncertainty is lower than 25% of the assembly tolerance. The combination of LT and articulated CMM successfully finishes the inspection task of the external guideway assembly. The assembly errors of the external guideway are mainly distributed in [] mm and can satisfy its assembly requirements. These results indicate that the proposed method is appropriate for the reconstruction of EAST. AcknowledgmentsThis research is supported by National Natural Science Foundation of China (Grant No. 51075117) and Project 111. The authors would like to thank all other members of the research team for their contributions to this project. ReferencesG. N. Peggset al.,
“Recent developments in large-scale dimensional metrology,”
J. Eng. Manufact., 223
(6), 571
–595
(2009). http://dx.doi.org/10.1243/09544054JEM1284 0954-4054 Google Scholar
Q. R. Zhao,
“Research on the Assembly and its Survey Systems for the EAST Superconducting Tokamak Device,”
,
(2004). Google Scholar
S. T. Wu,
“An overview of the EAST project,”
Fusion Eng. Design, 82
(5), 463
–471
(2007). http://dx.doi.org/10.1016/j.fusengdes.2007.03.012 FEDEEE 0920-3796 Google Scholar
S. T. Wu,
“EAST machine assembly and its measurement system,”
Fusion Eng. Design, 73
(2), 135
–140
(2005). http://dx.doi.org/10.1016/j.fusengdes.2005.04.002 FEDEEE 0920-3796 Google Scholar
Y. G. Ni,
“The establishment and application of real time measuring system for steel column hosting with total station,”
Geotech. Investig. Survey., 3 45
–48
(1998). Google Scholar
D. M. Gaoet al.,
“Some technology issues for the general assembly of EAST superconducting Tokamak,”
Fusion Eng. Design, 82
(5), 567
–574
(2007). http://dx.doi.org/10.1016/j.fusengdes.2007.02.012 FEDEEE 0920-3796 Google Scholar
S. T. Wuet al.,
“Recent main events in applied superconductivity in China,”
IEEE Trans. Appl. Supercond., 19
(3), 1069
–1080
(2009). http://dx.doi.org/10.1109/TASC.2009.2019244 ITASE9 1051-8223 Google Scholar
S. Aguadoet al.,
“Towards an effective identification strategy in volumetric error compensation of machine tools,”
Meas. Sci. Technol., 23
(6), 065003
(2012). http://dx.doi.org/10.1088/0957-0233/23/6/065003 MSTCEP 0957-0233 Google Scholar
J. Santolariaet al.,
“Articulated arm coordinate measuring machine calibration by laser tracker multilateration,”
Sci. World J., 2014 1
–11
(2014). http://dx.doi.org/10.1155/2014/681853 THESAS 1537-744X Google Scholar
J. Liet al.,
“A kinematic model for parallel-joint coordinate measuring machine,”
J. Mech. Robotics, 5
(4), 044501
(2013). Google Scholar
G. P. Greeff,
“A Study for the Development of a Laser Tracking System Utilizing Multilateration for High Accuracy Dimensional Metrology,”
,
(2010). Google Scholar
J. R. Linet al.,
“Establishment of precise three-dimensional coordinate control network in field large-scale measurement,”
J. Mech. Eng., 48
(4), 6
–11
(2012). http://dx.doi.org/10.3901/JME.2012.04.006 JENMDT 0733-9399 Google Scholar
D. ZhangS. RoltP. G. Maropoulos,
“Modelling and optimization of novel laser multilateration schemes for high-precision applications,”
Meas. Sci. Technol., 16
(12), 2541
–2547
(2005). http://dx.doi.org/10.1088/0957-0233/16/12/020 MSTCEP 0957-0233 Google Scholar
Z. M. Tonget al.,
“Industrial measurement system based on laser tracker and coordinate measurement arm,”
Meas. Tech., 5 13
–16
(2008). MSTCAL 0543-1972 Google Scholar
Y. Q. Guet al.,
“Combined large-scale measuring techniques in application of the EAST device,”
Tool Eng., 46
(3), 63
–66
(2012). Google Scholar
W. T. Estleret al.,
“Large-scale metrology–an update,”
CIRP Ann. Manufact. Technol., 51
(2), 587
–609
(2002). http://dx.doi.org/10.1016/S0007-8506(07)61702-8 0007-8506 Google Scholar
G. X. Zhanget al.,
“A study on the optimal design of laser-based multi-lateration systems,”
CIRP Annals-Manufact. Technol., 52
(1), 427
–430
(2003). http://dx.doi.org/10.1016/S0007-8506(07)60617-9 0007-8506 Google Scholar
BiographyLiandong Yu is the acting dean of the School of Instrument Science and Optoelectronic Engineering in HFUT. He received his PhD in precision engineering from HFUT in 2003. From September 2001 to September 2002, he was invited by PTB as guest scientist. He is the member of China Metrology Society and member of the National Optical Standards Committee. His research interests are polar CMM and nanometer measurement system. Huning Zhao is a PhD candidate in measuring and testing technologies and instruments for HFUT (China) in 2014. He received his MS degree in measuring and testing and technologies and instruments from HFUT (China) in 2014. His research interest is coordinate measuring technology. Wei Zhang is a PhD candidate in measuring and testing technologies and instruments of HFUT in 2013. He received his MS degree from Anhui University of Science and Technology (China) in 2013. His main interests are coordinate measurement technology and automatic measurement and control technology. Weishi Li is the Huangshan scholar professor in the School of Instrument Science and Optoelectronics Engineering, HFUT. He received his PhD from Zhejiang University (China) in 2002. Before joining HFUT, he was engaged in reverse engineering research at the Institute of High Performance Computing, Singapore and Cardiff University, respectively. His main interests are free-form inspection, reverse engineering, and computational metrology. Huaxia Deng is the Huangshan young scholar professor in the School of Instrument Science and Optoelectronics Engineering, HFUT (China). He received his PhD in engineering from the University of Liverpool, United Kingdom, in 2011. He is a member of the Institute of Physics. His research interests are analysis, measurement, and control of dynamic systems. |