|
|
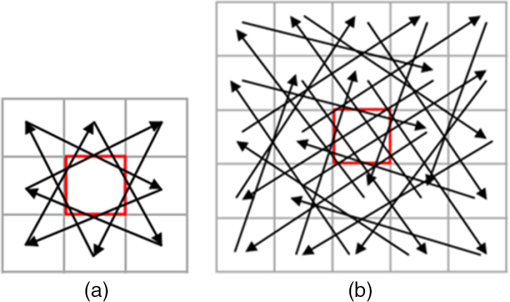
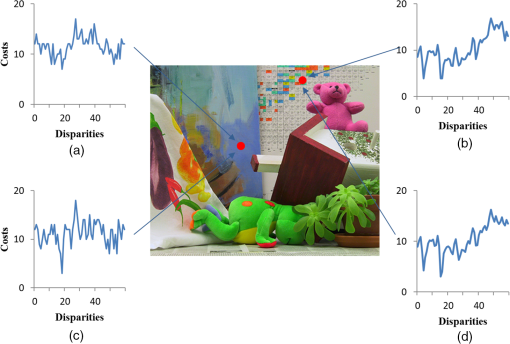
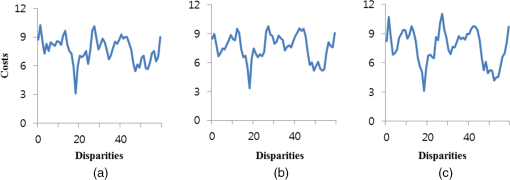
1.IntroductionStereo vision establishes the correspondence between both views as stereo matching and calculates the dense disparity and three-dimensional (3-D) depth information. The stereo matching method is largely divided into two parts: local and global. Also, the stereo matching algorithm consists of several steps, including initial matching cost calculation, cost aggregation, cost calculation, and refinement.1 The local method applies a matching window to find the correspondence between the reference image and the target image. It is more efficient than the global method because it searches only the designated area, whereas the global method explores the entire image area including the neighborhood area. The global method defines an energy model by using various conditions, such as uniqueness and continuity, and determines the matching information by minimizing the energy function of an entire image. The global method can obtain more exact difference values than the local method because it processes a search of the entire image repeatedly. However, the implementation of the global method is complex and is not suitable for real-time processing due to the amount of computational complexity. Representative examples of the global method include belief propagation,2,3 graph-cut,4 and dynamic programming.5 For noise robustness in stereo matching, we improve the original census transform (CT), which is one of the most widely used local methods to calculate the initial matching cost. Hirshmüller and Scharstein6 compared the performance of various stereo matching algorithms including CT, based on the image change due to different camera exposures and light conditions. CT compares the relative brightness between two pixels and converts the comparison result into a bit-string. The local methods, such as sum of absolute or squared difference and normalized cross correlation, compare the values of all pixels in the matching window. CT obtains a robust result toward brightness change and radiometric distortion because it determines only the relative high and low level of brightness between two pixels.7 However, CT is noise-sensitive because it compares the relative difference of brightness of a pixel with neighborhood pixels based on one single central pixel. In other words, the probability of false matching greatly increases when the central pixel is affected by noise or other conditions.8,9 Several suggestions have been proposed, such as the mini-census transform (MCT)8 and generalized-census transform (GCT),9 to improve the performance of the existing CT. CT compares all the pixels in the neighborhood based on the central pixels within the matching window; thus, if the size of the matching window increases, the computational complexity also increases. MCT compares only six pixels of the neighborhood, which are selected empirically, with a central pixel.8 This method has shown good performance with less computational complexity than the existing CT. Furthermore, GCT was proposed for robust matching performance toward Gaussian noise.9 This method applies pixels separated by a certain distance within the matching window, not the central pixel. MCT has a drawback whereby it is affected by noise due to the characteristic of comparing the brightness values of neighborhood pixels based on a single central pixel. On the other hand, GCT is robust to noise because it compares the neighborhood pixels to each other and the pixels are symmetrically set within a matching mask. This paper introduces star-census transform (SCT), which compares the pixels separated by a certain distance symmetrically. The purpose of the proposed method is to initiate the sampling of neighborhood pixels in a symmetrical pattern excluding the central pixels of the matching window. It then compares the previous and current sampling points consecutively along a scan pattern. Compared with GCT, which compares the brightness of sampling points separated by a certain distance, the proposed method is more robust to noise due to its comparison of brightness values between the sampling points. The sampling points and the distance (edge length) between these points can be diversely selected, depending on the correlation with the central pixel of the matching window, the degree of noise within the image, and the computational complexity requirement. The proposed SCT can be utilized in areas such as real-time stereo matching, as well as feature points matching and tracking. 2.Census TransformCT compares the brightness values between the pixels.6,7 Equations (1) and (2) show the CT equation and comparison process between brightness values. It describes the bit-string as a value compared by operator subjected to the brightness value of central pixel and the brightness value of neighborhood pixel in a matching window . Here, function returns 1 if the brightness value of the neighborhood pixel is higher than the counterpart of the central pixel, and 0 if the brightness value of the neighborhood pixel is lower than the counterpart of the central pixel by comparing the brightness values between pixels. is the encoding bit-string and consists of 0 and 1. It refers to a relative brightness distribution with neighborhood pixels on the basis of the central pixel of the window. The bit-string on the left reference image is computed, and then the bit-strings on the right target image are calculated within the search range of the maximum disparity of . If the matching window is , the bit-string is obtained. Also, as indicated in Eq. (3), the hamming distance value, which is implemented with exclusive logical OR arithmetic operation toward bit-strings of and , is calculated. Then, CT determines an initial difference value of pixel , which is equal to the lowest cost value of the difference value . MCT, which was proposed to reduce the computation complexity of the existing CT, compares only some parts of the pixels in the window based on the central pixel. In other words, on the sized matching window in Fig. 1(a), MCT only performs the comparison arithmetic operation of the six dark-colored pixels.8 GCT, in Fig. 1(b), is the CT method, which compares the neighborhood pixels with each other in a symmetrical pattern on the basis of the central pixel.9 GCT is more robust to noise than the other methods because it compares the brightness values of various neighborhood pixels in the direction of the arrow, not the central pixel. 3.Proposed Method3.1.Star-Census TransformThe existing CT compares the brightness values of the neighborhood pixels on the basis of the central pixel within the matching window; thus, if noise occurs, the false matching ratio greatly increases. The proposed SCT is a method used to compare the neighborhood pixels by symmetrical patterns in a consecutive manner, rather than comparing them with the central pixel. Here, it is crucial to select the sampling pixels, which are the subjects for comparison in the window. Fire and Archibald9 calculated the average degree of correlation between neighborhood pixels on the basis of the central pixel on Middlebury benchmark images: Tsukuba, Venus, Teddy, Cones, and so on. The result demonstrated that the highest correlation for the neighborhood pixels is shown for the distance of from the central pixel. Thus, checking the pixel area located 2 pixels from the central pixel of the matching window is an effective procedure for reducing the false matching. Based on this property, Fire proposed GCT, which compares the brightness values of neighborhood pixels in the symmetrical direction, without a central pixel. To reduce the noise that can arise from a particular location such as a central pixel, the proposed SCT samples the pixels separated by a certain distance within the matching window and compares the brightness values of the corresponding points. Also, the scan pattern of each sampling point should be designed symmetrically to obtain the same results even from a rotated image. Here, we employ the Chebyshev distance on a spatial space ( and coordinates), where the distance between two pixels is the greatest of their differences along any coordinate dimension. All the sample points for comparison in the matching window are connected, and the last sampling point is compared to the initial sampling point. In other words, the relative brightness heights of all sample points are analyzed along the scan pattern. The proposed method compares two neighborhood pixels consecutively on the basis of a random sample point in the matching window, so the matching accuracy is higher than that of the existing CT. Also, the initial sample point is compared to the last sample point. Thus, the scan pattern is connected as one line. This means that the distribution of the relative level of brightness values of all pixels can be measured. For example, a sized matching window can be compared with the sample points of the distance from 1 to 4, and the maximum distance increases depending on the size of the matching window. The proposed method can produce a variety of patterns depending on the size of the matching window, the compared distance between pixels, and the position of sampling points. Figures 2(a) and 2(b) show the SCT pattern with an edge length (comparison distance) of 2 in a matching window and an edge length (comparison distance) of 3 in a matching window: The proposed SCT can be defined by Eqs. (4) and (5). In Eq. (4), if the difference between brightness value of neighborhood pixel (excluding the central pixel of the matching window and the brightness value of of the neighborhood pixel , which is separated by a certain distance) is greater than 0, then it returns 1. Otherwise, the remaining pixels return 0. By using operator in Eq. (5), the comparison result of brightness values of pixels in the matching window of size is converted into a bit-string. The brightness values of the sampling points in a consecutive manner depending on the scan patterns in matching window are compared. The number of sampling points in which brightness has been compared is doubled in the same sized matching window, so it has a more robust performance for stereo matching. Figure 3 describes the average matching cost distribution obtained by CT and SCT, from two random areas (indicated in the red circle) of the Teddy image, which is the Middlebury standard image. These two areas are front-parallel planes, which face the camera and toward each other. The ground truth difference values of these two random areas are 18 and 15. Figures 3(a) and 3(b) show the distribution of matching cost from CT, and Figs. 3(c) and 3(d) show those from SCT. Figure 3(b) shows two minimum errors of the minimum cost values; it is therefore difficult to obtain exact disparity information. However, in Figs. 3(c) and 3(d), the minimum matching cost values are clearly obtained at 18 and 15 disparity levels, respectively. Figure 4 shows the matching cost distribution according to the edge length (the distance between the sample points) of SCT. In the case of the 24 sampling points in the matching window, there is no comparison pattern at the edge length of 4: pixels are sampled redundantly. We therefore sampled 16 points in the matching window in Fig. 4. The average matching cost in the marked areas of Fig. 3 (Teddy image) is then computed. In other words, Figs. 4(a)–4(c) indicate the cost error distribution with 16 sampling points in the matching window when the edge lengths are set to 2, 3, and 4, respectively. Compared to Fig. 4(c), the case of Fig. 4(a) is relatively easier to distinguish the location of the minimum matching cost. In this case, the edge length between sample points in the matching window is set as 2; we can thus obtain more reliable distribution of matching cost than in other cases. This result is consistent with the analysis result of the previous study.9 In the three cases shown in Fig. 4, peak-ratio naive (PKRN) is employed to measure the method of obtaining the reliable disparity value of the minimum matching cost obtained from the Winner Takes All method.10,11 PKRN determines the reliability of the final disparity value as Eq. (6), by calculating the proportion of the disparity value of the minimum matching cost () and the disparity value of the second minimum matching cost (). Generally, if the difference between and increases (if PKRN value becomes larger), it is determined that the reliable disparity value is obtained: where is a value for the case when the minimum matching cost () is 0 (). In Fig. 4, PKRN is used just to determine the reliability of the final disparity value according to three edge length parameters. in Eq. (6) has no influence on the matching performance.Table 1 describes the PKRN reliability results on the disparity value of Middlebury standard images (Tsukuba, Venus, Teddy, and Cones). When 24 points are sampled in a matching window, PKRN results by the SCT method are greater than those by the CT method. Here, “24-2-1” refers to the first of scan patterns with 24 sample points and the edge length of 2. Table 2 shows the PKRN results from inlier areas by a left–right consistency check. From Tables 1 and 2, the proposed SCT method with the edge length of 2 can obtain better reliable disparity information than the previous CT method. Table 1PKRN values of obtained disparity maps.
Table 2PKRN values of inlier disparity maps.
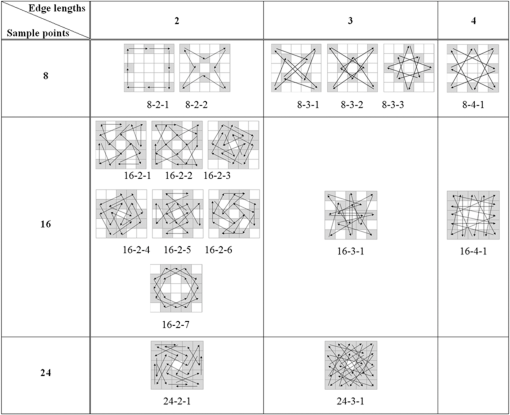
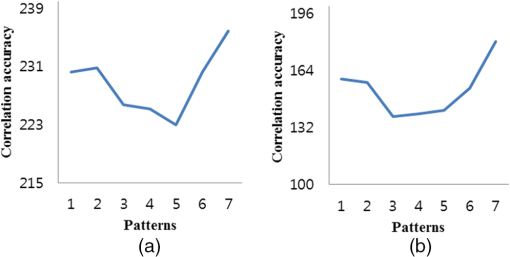
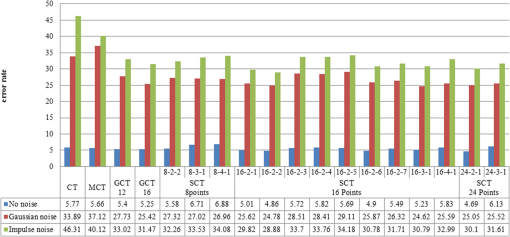
3.2.Selection of Sample PointsThe proposed SCT can perform a comparison operation up to 24 times in the matching window. When the matching window size increases, the number of bit-strings produced from the comparison operation increases. If the number of sampling points is reduced based on the scan pattern, the number of comparison operations also decreases. The edge length (comparison distance) in the matching window is 1 to 4. To ensure the accuracy and robustness against noise, the proposed method considers the patterns with edge lengths of 2 to 4, excluding the distance of 1. Figure 5 shows the possible patterns on the matching window according to the edge lengths and the number of sample points (shown as dark color). For example, if eight points are sampled, three patterns can be generated: (1) two scan patterns with the edge length of 2, (2) three scan patterns with the edge length of 3, and (3) one scan pattern with the edge length of 4. In Fig. 5, “8–2–1” refers to the first scan pattern with eight sample points and an edge length of 2. The initial sample point and the last sample point are connected, and the sample points are consecutively compared along their symmetrical pattern. Even if the edge lengths are same (if two pixels are separated by the same distance) in the matching window, we can choose several patterns, as shown in Fig. 5. When pixels in the matching mask are sampled, each point in the neighboring pixels has been correlated differently with a central pixel. Therefore, it is crucial to determine which pixel should be placed in a scan pattern in the area-based stereo matching window. Previous studies9 suggested the average correlation relationship between the central pixel and the neighborhood pixels on Middlebury standard images (Tsukuba, Venus, Teddy, and Cones). Based on this, it is possible to select the sample points with a high correlation relationship within the matching window. Figure 6 shows the average correlation calculated from each sample point along the seven different patterns (with 16 sample points and edge length of 2). The experiment results indicate that four patterns (16-2-1, 16-2-2, 16-2-6, and 16-2-7) show a high correlation, even if the Gaussian noise () is added. By employing appropriate scan patterns from the correlation distribution of an input image, we can improve the overall performance of stereo matching. 4.Experimental Results4.1.Benchmark Results AnalysisThe computer used in the experiment is Intel(R) Core(TM) i7-3770 CPU 3.40 GHz, Nvidia Geforce GTX 760. The Middlebury benchmark datasets12 for the performance test of stereo matching are employed. In the stereo matching framework, we compute an initial matching cost and apply cross-based aggregation13,14 of the initial costs in the support region. Then, a final disparity map is obtained using a median filter (Figs. 7 and 8). This experiment framework focuses on comparing the performance of the previous CT, MCT, and GCT methods with the proposed SCT method. If advanced cost aggregation and optimization processes are included, we can sufficiently obtain better stereo matching performance. Fig. 7Tsukuba, Venus, Teddy, and Cones images, ground truth, and disparity map obtained from proposed SCT: sample points of 8 (8-2-2), 16 (16-2-2), and 24 (24-2-1) (from left to right).  Fig. 8Baby 3, Bowling 2, Cloth 2, and Dolls images, ground truth, and disparity map obtained from proposed SCT: 8 sample points (8-2-2), 16 (16-2-2), and 24 (24-2-1) (from left to right).  Table 3 shows the false matching ratio of final disparity to ground truth in the nonocclusion regions by using the proposed SCT pattern (Fig. 5). A percentage of bad matching pixels is computed with the absolute difference between the computed disparity map and the ground truth disparity map. Here, a threshold value that means a disparity error tolerance is set to 1. Table 3Comparison of false matching ratio results (nonocclusion regions).
In Table 3, matching performance depends on both the scan pattern and the image local properties (intensity distribution) to some degrees. That means, there is no optimal scan pattern to guarantee the best matching performance in any input image. When SCT patterns with 8, 16, and 24 sample points and an edge length of 2 are employed, the most accurate matching performance is obtained. By considering the experimental results (Table 3), we can determine an appropriate scan pattern suitable for input images. Also, when comparing eight sampling points in the proposed pattern, the proposed SCT method showed better performance than the existing CT and MCT on the four benchmark images (Tsukuba, Venus, Teddy, and Cones). By using 16-2-2 patterns with 16 sample points on four benchmark images, the best performance with a 4.86% error percentage is obtained. In other reference images (baby 3, bowling 2, cloth 2, and dolls), the previous CT method achieved better stereo matching than MCT and GCT. In the proposed method, we obtained the best performance (5.10%) by using the 24-2-1 scan pattern with 24 sample points and an edge length of 2. In Table 3, best performance values according to the number of sample points (8, 16 and 24) are indicated in bold font. 4.2.Stereo Matching Performance in NoiseTo examine the noise robustness of the proposed method, Gaussian noise and impulse noise are applied to the Tsukuba, Venus, Teddy, and Cones images. Gaussian noise with a signal-to-noise ratio (SNR) of 10, 15, 20, 25, and 30 dB and an impulse noise with the pixel-to-noise ratio of 2, 5, 10, and 20% are applied, respectively. Table 4 shows the average false matching ratio results according to the amount of Gaussian noise (dB). If Gaussian noise exists, the existing CT and MCT methods obtain unreliable disparity maps overall, regardless of the amount of noise. Since Gaussian noise affects every pixel of the image evenly, the proposed method obtains reliable disparity results to some degree. When 16 sampling points are considered, the 16-3-1 scan pattern showed the best performance. Table 4False matching ratio in Gaussian noise (nonocclusion regions).
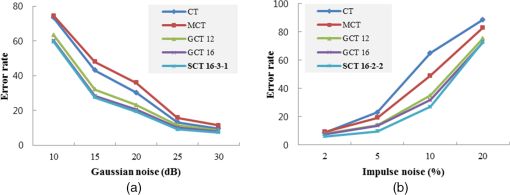
When Gaussian noise with a higher SNR (30, 25, and 20 dB) is added, the 24-2-1 scan pattern obtained the best performance. In addition, if Gaussian noise with a lower SNR (15 and 10 dB) is added, the 16-3-1 scan pattern achieves the best performance. In other words, for the case of relatively small noise, a more reliable disparity result by a scan pattern with more sampling points is obtained. In the image degraded much by Gaussian noise, we should choose patterns, which are suitable to identify the brightness distribution of the image.9 In the total average false matching ratio results, the best performance is obtained by using a scan pattern with 16 sampling points (16-3-1 and 16-2-2). In Table 4, best performance values according to the number of sample points (16 and 24) are indicated in bold font. Table 5 shows the average false matching ratio in Benchmark images (Tsukuba, Venus, Teddy, and Cones) with impulse noise. When an impulse noise of 2%, 5%, 10% and 20% is added, the average false matching ratio of GCT with an edge length of 16 is 31.47%, and that of the proposed SCT with a 16-2-2 pattern is 28.88%. In the case where impulse noise was applied in relatively small amounts (2%, 5%, and 10%), SCT showed much better performance than the other methods. When impulsive noise is significantly increased (20%), the performance of GCT was relatively better than that of the other methods. However, since the input stereo views are considerably degraded, it is difficult to obtain reliable disparity results. The error ratio by GCT is 72.75%. In Table 5, best performance values according to both the number of sample points (16 and 24) and the degree of impulse noise are indicated in bold font. Table 5 shows the best performance (24.78%) in average is obtained by using a 16-2-2 scan pattern. Table 5False matching ratio in impulse noise (nonocclusion regions).
Figures 9 and 10 show the average false matching results (Tables 4 and 5) by MCT, GCT, and proposed SCT when Gaussian noise and impulse noise are applied. The performance of CT and MCT is significantly affected by Gaussian noise and impulse noise. On the contrary, the proposed SCT shows relatively reliable stereo matching performance. In conclusion, in the case of stereo view with no noise (Benchmark images), the best performance is obtained by using SCT with an edge length of 2. If Gaussian noise is applied, we obtain the best reliable disparity map by using SCT with an edge length of 3. These results are consistent with the correlation distribution of the center pixel and neighborhood in the matching window.9 In Tables 4 and 5, we have evaluated matching performance both in Gaussian noise and in impulse noise with several SNR conditions. From the evaluation results (Tables 4 and 5), we determine the scan pattern with 16 sample points in a matching window to cope with practical situation, where the noise is generated in image acquisition. These results are consistent with the correlation distribution of the center pixel and neighborhood in the matching window.9 In case a pixel belongs to a different surface other than the surface on which the kernel pixel is, the encoding result may be affected by local brightness distribution. Figure 11 shows the disparity results in no noise and Gaussian noise. In Fig. 11, the disparity value distribution at surface discontinuities is indicated in the red rectangle. Some foreground regions become thicker (about one pixel) at surface discontinuities than ground truth depths. However, Table 6 shows that SCT obtains more reliable initial disparity results even at surface discontinuities than the existing CT. Here, the first scan pattern with 24 sample points and an edge length of 2 (24-2-1) is employed. The performances are evaluated in the nonoccluded region “non-occ,” all (including half-occluded) regions “all,” and regions near depth discontinuities “disc” region, respectively. Fig. 11Disparity maps by [(a) and (c)] existing CT [(b) and (d)] and by SCT in no noise and Gaussian noise (Table 6).  Table 6False matching ratio of initial disparity maps.
In conclusion, though matching results at surface discontinuities may be affected by coplanarity of the central point of the search window and the sample points, overall performance by SCT is much more reliable than the existing CT. 5.ConclusionThis paper presents an improved CT method with a star-like scan pattern. The brightness values of the sampling points separated by a certain distance within the stereo matching window are compared in a symmetrical manner. The drawback of the existing CT is that the computation complexity increases: as the matching window size increases, the number of conversed bit-strings also increases. In the proposed SCT, we can choose an appropriate scan pattern in accordance with the processing speed, correlation distribution of the subject image, and types of noise. From the experiment results in Gaussian noise and impulse noise, the proposed SCT achieved relatively more reliable matching performance, even when using smaller sample points than those of the existing methods. The proposed method is also useful in other areas, such as feature matching and tracking. AcknowledgmentsThis work was supported by Basic Science Research Program through the National Research Foundation of Korea (NRF) funded by the Ministry of Education, Science and Technology (Grant No. 2013R1A1A2008953). ReferencesD. Scharstein and R. Szeliski,
“A taxonomy and evaluation of dense two-frame stereo correspondence algorithms,”
Int. J. Comput. Vision, 47
(1), 7
–42
(2002). http://dx.doi.org/10.1023/A:1014573219977 IJCVEQ 0920-5691 Google Scholar
A. Klaus, M. Sormann and K. Karner,
“Segment-based stereo matching using belief propagation and a self-adapting dissimilarity measure,”
in Proc. of Int. Conf. on Pattern Recognition,
15
–18
(2006). Google Scholar
Q. Yang et al.,
“Stereo matching with color-weighted correlation, hierarchical belief propagation, and occlusion handling,”
IEEE Trans. Pattern Anal. Mach. Intell., 30
(3), 492
–504
(2008). http://dx.doi.org/10.1109/TPAMI.2008.99 ITPIDJ 0162-8828 Google Scholar
J. Worby and W. J. MacLean,
“Establishing visual correspondence from multi-resolution graph cuts for stereo-motion,”
in Proc. of Computer Vision and Pattern Recognition,
313
–320
(2007). Google Scholar
M. Gong and Y. Yang,
“Real-time stereo matching using orthogonal reliability-based dynamic programming,”
IEEE Trans. Image Process., 16
(3), 879
–884
(2007). http://dx.doi.org/10.1109/TIP.2006.891344 IIPRE4 1057-7149 Google Scholar
H. Hirschmüller and D. Scharstein,
“Evaluation of stereo matching costs on images with radiometric differences,”
IEEE Trans. Pattern Anal. Mach. Intell., 31
(9), 1582
–1599
(2009). http://dx.doi.org/10.1109/TPAMI.2008.221 ITPIDJ 0162-8828 Google Scholar
R. Zabih and J. Woodfill,
“Non-parametric local transforms for computing visual correspondence,”
in Proc. of European Conf. on Computer Vision,
151
–158
(1994). Google Scholar
N. Chang et al.,
“Algorithm and architecture of disparity estimation with mini-census adaptive support weight,”
IEEE Trans. Circuits Syst. Video Technol., 20
(6), 792
–805
(2010). http://dx.doi.org/10.1109/TCSVT.2010.2045814 ITCTEM 1051-8215 Google Scholar
W. Fire and J. Archibald,
“Improved census transforms for resource-optimized stereo vision,”
IEEE Trans. Circuits Syst. Video Technol., 23
(1), 60
–73
(2013). http://dx.doi.org/10.1109/TCSVT.2012.2203197 ITCTEM 1051-8215 Google Scholar
X. Hu and P. Mordohai,
“Evaluation of stereo confidence indoors and outdoors,”
in Proc. of Computer Vision and Pattern Recognition,
1466
–1473
(2010). Google Scholar
D. Pfeiffer, S. Gehrig and N. Schneider,
“Exploiting the power of stereo confidences,”
in Proc. of Computer Vision and Pattern Recognition,
297
–304
(2013). Google Scholar
D. Scharstein, R. Szeliski and H. Hirschmüller,
“Middlebury stereo vision,”
(2015) http://vision.middlebury.edu/stereo/ December ). 2015). Google Scholar
K. Zhang, J. Lu and G. Lafruit,
“Cross-based local stereo matching using orthogonal integral images,”
IEEE Trans. Circuits Syst. Video Technol., 19
(7), 1073
–1079
(2009). http://dx.doi.org/10.1109/TCSVT.2009.2020478 Google Scholar
X. Mei et al.,
“On building an accurate stereo matching system on graphics hardware,”
in Proc. of IEEE Int. Conf. on Computer Vision Workshops on GPUs for Computer Vision,
467
–474
(2011). http://dx.doi.org/10.1109/ICCVW.2011.6130280 Google Scholar
BiographyJongchul Lee received his BS degree in computer engineering from Academic Credit Bank System, Seoul, Republic of Korea, in 2007. He is currently pursuing a MS degree in the Department of Imaging Science and Arts, Graduate School of Advanced Imaging Science, Multimedia and Film (GSAIM) at Chung-Ang University, Seoul. His research interests include stereo vision, computer vision, and augmented reality. Daeyoon Jun received his BS degree in electronic software engineering from Hansei University, Gunpo, Republic of Korea, in 2015. He is currently pursuing a MS degree in the School of Integrative Engineering, Chung‐Ang University, Seoul, Republic of Korea. His research interests include stereo vision and computer vision. Changkyoung Eem received his BS, MS, and PhD degrees in electronic engineering from Hanyang University, Republic of Korea, in 1990, 1992, and 1999, respectively. From 1995 to 2000, he worked at DACOM R&D Center. In 2000, he founded a network software company, IFeelNet Co., and worked for Bzweb Technologies as CTO from 2006 to 2009 in the United States. Since 2014, he has been an industry university cooperation professor at Chung-Ang University, Republic of Korea. His research interests include stereo vision, computer vision, and augmented reality. Hyunki Hong received his BS, MS, and PhD degrees in electronic engineering from Chung-Ang University, Republic of Korea, in 1993, 1995, and 1998, respectively. From 1998 to 1999, he worked as a researcher in the Automatic Control Research Center, Seoul National University, Republic of Korea. From 2000 to 2014, he was a professor in GSAIM at Chung-Ang University. Since 2014, he has been a professor in the School of Integrative Engineering, Chung-Ang University. His research interests include stereo vision, computer vision, and augmented reality. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||