|
|
1.IntroductionCharged-couple devices (CCD) and complementary metal oxide semiconductor (CMOS) image sensors have become standard beam radius measurement tools due to their ability to return a two-dimensional (2-D) beam intensity profile. The first-order moment (arithmetic centroid) has been used with CCD sensors to track the position of lasers,1 Shack–Hartman wavefronts,2 and stars.3 From values such as second moment beam diameter, beam ellipticity, and beam orientation, more complex propagation related beam quality metrics such as may be determined.4–6 We note that for a pure Gaussian beam, the second moment radius equals the (13.53%) radius determined by percent-of-peak intensity. Although previous literature has dealt primarily with the CCD sensor, CMOS sensors are quickly replacing CCD sensors as they are more economical to produce and require less power.7 The second moment beam radius measurement technique, in conjunction with the CCD or CMOS sensor, improves on simpler beam profiling devices, which return only a one-dimensional (1-D) beam intensity profile through use of a scanning slit or knife edge. The beam radius on the scanning beam profilers is calculated by finding the radius at which the beam’s 1-D intensity profile intersects a predetermined percentage (e.g., 13.53%) of the beam’s peak intensity.8 Although a similar method can be used with CCD or CMOS sensors, the second moment utilizes the full 2-D beam profile, providing a more accurate beam measurement technique. The radius of the monochromatic beam is given by the second moment as5 is defined as where is the radius extending from the center of the beam, is the beam’s axis of propagation, and is the beam’s time-averaged intensity distribution. This paper addresses only monochromatic beams, thus forgoing the use of the second moment polychromatic beam radius definition.9In the past, image sensors were avoided for beam measurement since high noise levels from background light photon noise, readout noise, background level, and sampling error10 were problematic when coupled with the second moment measurement method, which is highly susceptible to error from noise. However, the last two decades have seen improvements to image sensor hardware and the development of noise reduction techniques, which enable image sensors to provide accurate beam radius measurements. The noise reduction techniques can be understood by considering the second moment integrals [see Eq. (2)], which heavily weight noise at high values of .11 If—for a theoretical sensor—the limits of extended toward infinity, then the second moment integral would be completely dominated by noisy pixels.12 Even with finite dimensions, noise at high values and outside the beam area can adversely affect the accuracy of small beam measurements. Two techniques are generally used to reduce noise. In the first method, pixels below a certain threshold value are removed from the second moment calculation (thresholding) in an attempt to retain only valid beam data.13 However, noisy pixels falling above the threshold value can remain. Therefore, the second technique limits the region about the centroid over which the summation occurs (software aperture) to further reduce the second moment error due to noise.14 The thresholding algorithm is applied to the image sensor data before using a software aperture or calculating the second moment.13 Thresholding entails first sampling an unilluminated portion of the sensor (e.g., the four corners) to determine the mean and standard deviation of the background noise. The mean and standard deviation are then used to calculate a threshold value against which each pixel’s intensity value is compared. Pixels falling below the threshold value are considered unilluminated, whereas pixels above the threshold have the mean subtracted from their intensity value and are then used in the second moment calculation. A pixel is considered illuminated when where according to the ISO 11146 standard.13 If is set too low, noisy pixels are considered illuminated, but if is set too high then valid beam data are lost (see Fig. 1). Therefore, there exists an optimum value of for which noise is excluded from the beam measurement but at which the beam truncation is minimal.10 Regardless of the value , some portion of a noisy beam is truncated by the thresholding procedure.Fig. 1(a) 1-D Gaussian intensity distribution (solid line). Pixels below the threshold level [dotted line, Eq. (3)] are considered unilluminated. The corresponding threshold radius [dash-dot line, Eq. (8)] denotes the truncation of the Gaussian beam by thresholding, so the beam intensity data to the right of the threshold radius is not used in subsequent calculations—including the calculation of the software aperture. The software aperture radius [dashed line, Eq. (12)] shows the final truncation of the Gaussian beam after both thresholding and the software aperture are applied. Only beam intensity data to the left of the software aperture radius is used in the second moment calculations. The thresholding level, threshold radius and software aperture radius are set to arbitrary values to demonstrate truncation. In actuality, the threshold level moves up-down (denoted by double-headed arrows) depending on the present noise levels, which give a corresponding left-right shift to the threshold radius. Furthermore, the software aperture radius moves left-right depending on the software aperture conditions set in the beam analysis software. 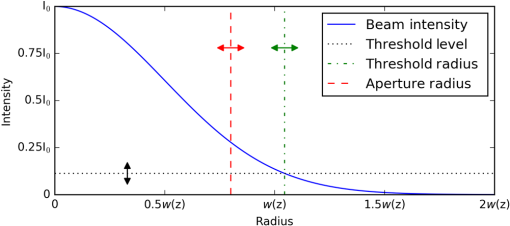 After thresholding, the software aperture can be applied to exclude extraneous noise from the second moment calculation yet retain valid beam data. The software aperture is centered on the beam and extends a finite distance from the centroid [see Fig. 2(b)]. While the software aperture removes noise, it also truncates the tails of the Gaussian beam (see Fig. 1), and a balance must be struck between eliminating extraneous noise and removing valid data.15 Theoretical work and simulations have shown that the optimal software aperture size varies with both the value used in thresholding14 and the radius of the beam.11 Although is predetermined, the beam radius is generally not known before measurement, and an iterative algorithm must determine the optimal software aperture size for the measured beam.5 Fig. 2(a) A elliptical Gaussian intensity distribution in region surrounded by the software aperture (solid line). (b) The elliptical Gaussian intensity distribution from (a) transformed into a radially symmetric Gaussian distribution in region with the inclusion region (solid line) transformed as well. A radially symmetric intensity distribution and software aperture are needed in the scale factor derivation to return analytic solutions from the second moment integrals. 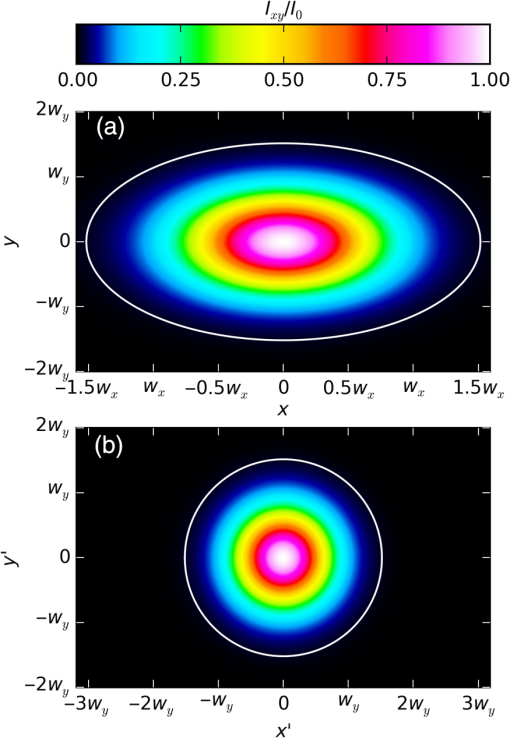 An elliptically invariant scale factor that corrects for the truncation of a Gaussian beam by both thresholding and the software aperture is derived in this paper. Since a scale factor must be based on the expected beam,15 we use the ubiquitous Gaussian, which has a time-averaged intensity profile represented by where is the peak intensity of the beam, is defined as and is the radius of the beam when the intensity is .2.Scale Factor DerivationThe scale factor derived herein corrects for the truncation of the Gaussian beam by both thresholding and the software aperture. To derive the scale factor, three main steps are needed. First, the radius (threshold radius) at which the Gaussian beam is truncated by thresholding alone must be determined. This value is then used to calculate the software aperture radius—where the beam is truncated by both noise reduction techniques. Finally, the software aperture radius is applied to the second moment integrals, which yields an analytic solution and allows the scale factor to be determined through algebraic manipulation. 2.1.ThresholdingThresholding is performed on the sensor data before the software aperture is applied or the second moment is calculated. For ease of calculation, the standard deviation of the noise is rewritten as the peak beam intensity multiplied by a scalar After the threshold comparison has been applied, the mean is subtracted from the illuminated pixels. The radius at which the Gaussian intensity distribution is truncated by thresholding can then be found by setting equal to the threshold value Solving Eq. (7) for yields2.2.Software ApertureThe software aperture is applied after thresholding to include valid beam data and exclude extraneous noise from the second moment calculations. Although previous work has focused on a square or rectangular software aperture,12,13 a radially symmetric software aperture (for a radially symmetric beam) has the advantage of excluding extraneous noise found in the corners of a rectangle or square. We define the software aperture as a circular region centered on the beam, which includes a portion of the sensors total power after thresholding. is given as where is the power within the software aperture. To calculate and , the equation for power is used Nominally, the radius limit would extend to infinity for ; however, thresholding truncates the beam before the software aperture’s application, so the beam’s remaining power is contained within the radius . Thus, for the total power, . For the power in the software aperture, , where is the radius of the software aperture. Now Eq. (9) can be rewritten with Eq. (8) replacing . Solving Eq. (11) for yields where is defined as Equation (12) gives the radius at which the Gaussian beam is truncated by both thresholding and the software aperture (see Fig. 1).2.3.Scale FactorTo find the radius of the beam, Eq. (2) is first rewritten with integration limits defined by the software aperture Evaluating the integral in the numerator gives whereas the integral in the denominator yields Substituting Eqs. (15) and (16) into Eq. (14) and simplifying gives Next, we solve Eq. (17) for in terms of by substituting Eq. (12) for Now, the second moment radius is found by substituting Eq. (18) into Eq. (1) and replacing with Eq. (5) Solving Eq. (19) for the actual beam radius in terms of gives where is the scale factor defined by Thus, the second moment radius—subject to systematic error from truncation—can be multiplied by the scale factor (see Fig. 3) to give the beam radius devoid of truncation error. The variables in are either predetermined or found using beam analysis software, thereby allowing the scale factor to be calculated for a measured beam.Fig. 3(a) Scale factor as a function of [see Eq. (21)], which corrects for truncation of the Gaussian beam by both thresholding and the software aperture. Values of represent a significant uncorrected error that should be addressed by either tuning the noise reduction settings or reducing the actual noise on the sensor. Note that, as expected, the scale factor goes to one as goes to one [see Eq. (24)]. 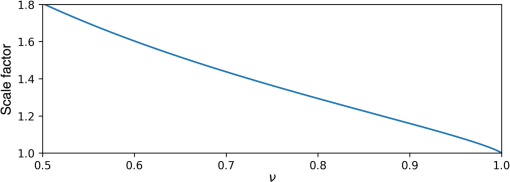 Although the scale factor accounts for both thresholding and the software aperture, it simplifies when only one noise reduction technique is used (either thresholding or the software aperture). If only thresholding is used, and , so the scale factor reduces to Conversely, when only the software aperture is applied, and . Thus, the scale factor becomes If neither thresholding nor the software aperture is used, the limit as goes to one and goes to zero yields Equation (20) can then be rewritten with replaced by Eq. (24) as which is the expected result since the Gaussian beam is truncated by neither thresholding nor the software aperture.It can be shown (see Appendix A) that the scale factor is invariant to the ellipticity of the beam. However, to find analytical solutions to the second moment integrals, the scale factor derivation must be performed with a radially symmetric Gaussian intensity distribution and the polar second moment equations. Therefore, an elliptical intensity distribution in region is rewritten as a radially symmetric distribution in the new region (see Fig. 2) through use of a linear transform. The scale factor derivation demonstrated above is then performed in region with the polar second moment equations. After transforming from region back to , the scale factor has the same form as Eq. (21) and corrects the second moment calculated radii along both the and axes. 3.TestingBoth simulations and real beam data were used to test the scale factor. Whereas simulations provided a more in-depth analysis of the scale factor’s effectiveness—by comparing the measured beam radii to the actual beam radii, determined a priori—the analysis of real beam data was needed to demonstrate the efficacy of the scale factor in real-world applications. However, since the radius of a real beam cannot be predetermined, the noise reduction parameters ( and ) were varied during measurement to show that radii corrected by the scale factor are invariant to and as derived. 3.1.SimulationsSimulated laser beams were generated to test the scale factor’s effectiveness and invariance to ellipticity by comparing the generated radii to the measured radii and determining the error in the measured radii. The beams were simulated on a 16-bit sensor of , with each pixel’s length and width equal to . Although most image sensors are 12 bit, error from analog-to-digital quantization can be ignored when using a 16-bit sensor.14 The beams were generated with the beam’s peak amplitude scaled to , where is the total analog-to-digital converter levels for a sensor (i.e., for a 16-bit sensor). Beam analysis software calculated the second moment radii of the generated beams and allowed thresholding and the software aperture to be turned on or off independently. Thresholding was applied with (the scalar of the standard deviation of the noise) set to 4 (highest allowable value per the ISO 11146 standard). Generally, is optimized to sufficiently threshold noise yet minimize beam truncation; however, the scale factor corrects error due to truncation, allowing high values of —which remove more noise—to be used. The software aperture radius (or major and minor axes for an ellipse) was iterated by the software until which corresponds to an aperture radius roughly 1.5 times the beam radius. When both thresholding and the software aperture were turned on, the software aperture radius was calculated after thresholding had been applied.Due to the layout of the image sensor’s pixels as a rectangular grid, the second moment equations in Cartesian coordinate form, rather than polar coordinate form, were used. Since, for the beams generated, the angle between the measurement axes and the beam axes was zero, the second moment equations for the beam radii simplified to16 where and for a discretized intensity distribution are given by The and centroids are defined as with and each equal to . Equations (27) and (28) were each multiplied by the scale factor (calculated via the beam analysis software for each beam) to give the corrected beam radius. The analysis software’s calculated radii (with and without the scale factor) were compared to the generated beam’s actual radii to determine the percent error. We postulated that the calculated radii corrected by the scale factor would return a smaller percent error than the uncorrected radii and that the scale factor would correct the radii values irrespective of the beam’s ellipticity.Three sets of radially symmetric beams were generated and analyzed with different noise reduction settings to characterize the effectiveness of the scale factor. Whereas the first set of beams used only thresholding and the second set of beams applied only the software aperture, the third set of beams employed both thresholding and the software aperture together. Gaussian noise with a mean of and a standard deviation of was added to the first and third set of beams to simulate noise on the image sensor. The values for and were chosen to reflect the noise levels seen when measuring real beam data. Since, the second set of beams was analyzed without thresholding, the scale factor reduced to Eq. (23) and had no dependence on noise; therefore, for these beams, no noise was added. The error of the corrected radii was over an order of magnitude lower than the error of the uncorrected radii across all three sets of calculated beam radii. The error for the first set of calculated beam radii exhibited exponentially decaying behavior and became asymptotic at a radius of [see Fig. 4(a)] with an average error of 3.46% and 0.07% for the uncorrected and corrected beams, respectively. The smaller beams had fewer illuminated pixels, and the noise left after the thresholding process dominated the second moment calculation, which led to high errors. For the second set of beams, the error was approximately constant with an average of 2.41% for the uncorrected radii and 0.20% for the corrected radii [see Fig. 4(b)]. The third set of beams showed exponential decay, which reached an asymptote around with an average uncorrected error of 5.24% and a corrected error of 0.05% [see Fig. 4(c)]. Although the large error for the smaller beams was similar to the first set of beams (thresholding only), the software aperture removed outlying noisy pixels, which significantly reduced the error compared to thresholding alone. Fig. 4(a) The radius percent error as a function of the beam radius with only thresholding applied. Both the uncorrected error (triangle) and the corrected error (diamond) showed decaying exponential behavior, but quickly became asymptotic around with average errors of 3.46% and 0.07%, respectively. (b) The radius percent error as a function of the beam radius using only the software aperture. The uncorrected error (triangle, average error 2.41%) and the corrected error (diamond, average error 0.20%) were approximately constant for the various beam radii. (c) The radius percent error as a function of the beam radius with both thresholding and the software aperture applied. The error decayed exponentially, reaching the asymptote around , but with an error significantly lower than in (a). Although the uncorrected error (triangle, average error 5.24%) for the asymptotic region was higher than in (a) and (b), the corrected error (diamond, average error 0.05%) was of similar magnitude. For (a)–(c), the error from beam radius measured along the axis and the error from the beam radius measured along the axis were averaged to give a single error value. In (a) and (c), the beams were generated and measured 10 times at each point to give the average and standard deviation (error bars). The beams in (b) were only measured once since they contained no noise. 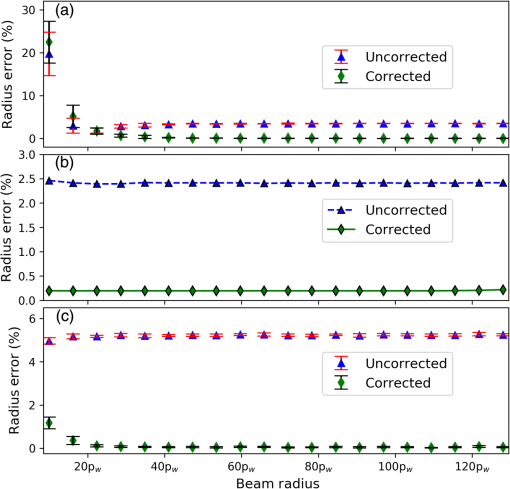 Whereas the first and second tests demonstrated that the scale factor independently corrects for beam truncation due to either thresholding or the software aperture, the third test showed it can correct for them simultaneously. Indeed, thresholding and the software aperture were needed in conjunction since thresholding alone was unable to return accurate beam measurements for the small beams. Although the uncorrected error was significantly higher when both thresholding and the software aperture were used (due to the combination of systematic errors), the corrected error was of similar magnitude as the corrected error when only thresholding or the software aperture were employed. Finally, a set of elliptical beams was generated with Gaussian noise ( and ) to determine whether the scale factor is, as derived, invariant to the ellipticity of the Gaussian beam (see Fig. 5). The generated beams had ellipticities () ranging from 0.08 to 1.00, and their second moment radii were calculated after both thresholding and the software aperture had been applied. The error for the corrected radii was approximately constant as the beam ellipticities changed (see Fig. 5), and the scale factor reduced the error from an average of 5.23% (uncorrected) to 0.06% (corrected). Although slight variations were seen in the corrected error, these were due to the random Gaussian noise in the beams rather than changes in ellipticity. The significant reduction in beam radius error coupled with the consistency of the corrected error, with respect to the changes in ellipticity, demonstrated that the scale factor corrects for the truncation of a Gaussian beam irrespective of ellipticity. Fig. 5The radius percent error as a function of the beam ellipticity with both thresholding and the software aperture applied. Both the uncorrected error (triangle, average percent error 5.23%) and the corrected error (diamond, average percent error 0.06%) were approximately constant with varying beam ellipticity. The beams were generated and measured ten times at each point to give the average and standard deviation (error bars). Finally, the error from beam radius measured along the axis and the error from the beam radius measured along the axis were averaged to give a single error value. 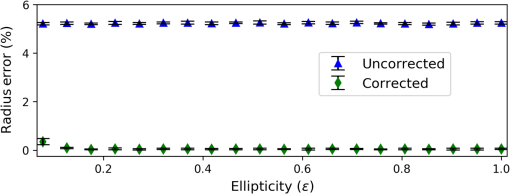 3.2.Real Beam DataSince the radius of a real laser beam is determined only through measurement and not known a priori, the measured radius cannot be compared to the exact radius as with the simulated beams. However, noting that the scale factor corrects for the second moment measurement’s dependence on the noise reduction parameters and [see Eq. (20)], we postulated that systematically varying the noise parameters would result in a varied uncorrected radius and a constant corrected radius. Furthermore, the invariance of the corrected radius to and reflected the physical description of a real laser beam—the radius of which does not change based on software parameters—and allowed the scale factor to be tested on real beam data with a predicted result. Two tests were implemented using a single mode Gaussian beam with a wavelength of 675 nm and a beam radius of measured on a 12-bit image sensor of (pixel height and width ) with the beam analysis software described in the simulation section. Whereas the first test used only thresholding with varied from 3.5 to 4 (for the effect of the scale factor is unobscured by noise), the second test used both thresholding and the software aperture with held constant at and evenly incremented from 0.985 to 0.995. The measured radii (both uncorrected and corrected) were divided by their initial radius values to show deviations from the initial values (Fig. 6). Fig. 6(a) Radius as a function of divided by the initial radius for both the uncorrected (triangles) and corrected radii (diamonds) with only thresholding applied. As was incremented, the uncorrected beam radius decreased and the corrected beam radius remained approximately constant. (b) Radius as a function of divided by the initial radius for both the uncorrected (triangles) and corrected radii (diamonds). Thresholding and the software aperture were both used, but was held constant at . The uncorrected beam radii increased as the value of increased (larger software aperture), whereas the corrected radii remained approximately constant. For both (a) and (b), the error from beam radius measured along the axis and the error from the beam radius measured along the axis were averaged to give a single error value. Additionally, the beam was measured 10 times at each point to give the average and standard deviation (error bars). 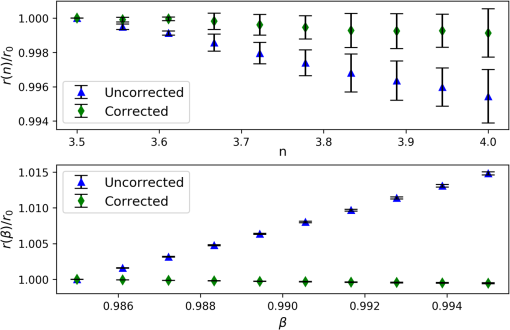 In both tests, the uncorrected radii decreased as the truncation of the beam increased (larger and smaller ); however, the corrected radii remained approximately constant, demonstrating that the radii corrected by the scale factor are invariant to changes in and as predicted. Furthermore, the tests—which were performed on real beam data—showed that the scale factor effectively corrects the second moment radius measurements in real-world application. 4.ConclusionAn image sensor (CCD or CMOS) in conjunction with the second moment radius analysis method can accurately measure the radius of a laser beam; however, the second moment method heavily weights noise and noise reduction techniques such as thresholding and a software aperture must be used before calculating the second moment beam radius. Even as these techniques reduce the random error due to noise, they simultaneously generate systematic error by truncating the tails of the Gaussian beam. A scale factor, invariant to the ellipticity of the beam, was derived to correct the second moment beam radius in response to this systematic error. Both simulations and real beam data were used to test the scale factor. Simulated laser beams tested the effectiveness of the scale factor and its elliptical invariance by comparing the measured beam radii—corrected and uncorrected—to the generated beams’ actual radii. The measured beam radii were calculated with three different noise reduction settings: only thresholding, only the software aperture, and both thresholding and the software aperture. With all three methods, the scale factor reduced the error of the measured radii by over an order of magnitude; thus, as predicted, the scale factor significantly improved the accuracy of the second moment beam radius measurements. Next, a set of elliptical beams was generated and the radii were measured with both thresholding and the software aperture applied. The corrected error of the beam radii was approximately constant as the ellipticity changed, proving that the scale factor is, as derived, invariant to beam ellipticity. Finally, the scale factor was tested with real beam data by systematically varying the values used in the noise reduction techniques. The observed behavior—the corrected radii remained constant, while the uncorrected radii changed—matched both the derived and physical predictions, thus demonstrating the scale factor’s effectiveness in real-world applications. Further simulations could be done to test the scale factor when either the noise levels are varied or the size of the simulated sensor is changed (e.g., 256, 1024, or 2048 pixels across). Additional theoretical work could be done to derive a scale factor that is valid for higher-order modes (i.e., Hermite–Gaussian beams and Laguerre–Gaussian beams). AppendicesAppendix A:Scale Factor Invariance for Elliptical Gaussian BeamsThe scale factor is invariant to the ellipticity of the beam as can be shown by transforming an elliptical beam in region to a radially symmetric beam in region and performing the scale factor derivation there. The time-averaged intensity of an elliptical Gaussian beam is given in a Cartesian coordinate system as where is the peak intensity, is the radius of the beam along the axis, and is the radius of the beam along the axis. A new region with coordinates and is formed from with a transform which yields and Substituting Eqs. (35) and (36) into Eq. (33) gives In polar coordinates, Eq. (37) can be written where is defined as Thus, the radially symmetric Gaussian intensity distribution in Eq. (4) is recovered with replaced by (see Fig. 2).Integrals are transformed when moving from to with the following equation:17 where is the Jacobian determinant given by and is defined as Equation (40) can be rewritten by changing to polar coordinates and substituting Eq. (41) for the Jacobian determinant Therefore, the transformation from region to region requires the integral to be multiplied by the scalar . However, the integrals in the scale factor derivation are always found as a ratio [Eqs. (2) and (9)], so the factor cancels out when the scale factor derivation is performed in region with the transformed elliptical Gaussian. Using the results of Eqs. (38) and (43), Eq. (18) becomes and using Eq. (1) Substituting Eq. (39) for and solving for gives Using Eqs. (42), (46) becomes Transforming from region back to region along the and axes yields where and are the measured second moment radii along the and axes, respectively. Substituting Eqs. (48) into (47) and Eqs. (49) into (46) gives Thus, the scale factor is invariant to the ellipticity of a Gaussian beam.AcknowledgmentsThe authors would like to thank Steve Garvey for his contributions to the numeric scale factor preceding the analytic scale factor and John Cadigan for his help with Python simulations. This work was supported by DataRay Inc. ReferencesR. P. Loce and R. E. Jodoin,
“Sampling theorem for geometric moment determination and its application to a laser beam position detector,”
Appl. Opt., 29
(26), 3835
–3843
(1990). http://dx.doi.org/10.1364/AO.29.003835 APOPAI 0003-6935 Google Scholar
M. Xia et al.,
“Shack-Hartmann wavefront sensor with large dynamic range,”
J. Biomed. Opt., 15
(2), 026009
(2010). http://dx.doi.org/10.1117/1.3369810 JBOPFO 1083-3668 Google Scholar
E. Dennison and R. Stanton,
“Ultra-precise star tracking using charge coupled devices (CCDs),”
in 24th Annual Technical Symp.,
54
–63
(1980). Google Scholar
A. Siegman,
“How to (maybe) measure laser beam quality,”
DPSS Lasers: Applications and Issues, 184
–199 Optical Society of America, Washington, D.C.
(1998). Google Scholar
“Lasers and laser-related equipment-test methods for laser beam widths, divergence angles and beam propagation ratios,”
(2005). Google Scholar
A. E. Siegman,
“New developments in laser resonators,”
Proc. SPIE, 1224 2
–14
(1990). http://dx.doi.org/10.1117/12.18425 PSISDG 0277-786X Google Scholar
N. Waltham,
“CCD and CMOS sensors,”
Observing Photons in Space, 423
–442 Springer, New York
(2013). Google Scholar
A. E. Siegman, M. Sasnett and T. Johnston,
“Choice of clip levels for beam width measurements using knife-edge techniques,”
IEEE J. Quantum Electron., 27
(4), 1098
–1104
(1991). http://dx.doi.org/10.1109/3.83346 IEJQA7 0018-9197 Google Scholar
L. Martí-López and O. Mendoza-Yero,
“Effect of chromatic aberration on gaussian beams: non-dispersive laser resonators,”
Opt. Laser Technol., 31
(3), 239
–245
(1999). http://doi.org/10.1016/S0030-3992(99)00047-X Google Scholar
X. Ma, C. Rao and H. Zheng,
“Error analysis of CCD-based point source centroid computation under the background light,”
Opt. Express, 17
(10), 8525
–8541
(2009). http://dx.doi.org/10.1364/OE.17.008525 OPEXFF 1094-4087 Google Scholar
T. S. Ross and W. P. Latham,
“Appropriate measures and consistent standard for high energy laser beam quality (postprint),”
Journal of Directed Energy, 2 22
–58
(2006). Google Scholar
T. S. Ross, Laser Beam Quality Metrics, SPIE Press, Bellingham, Washington
(2013). Google Scholar
“Lasers and laser-related equipment-test methods for laser beam widths, divergence angles and beam propagation ratios,”
(2004). Google Scholar
H. Yuanxing and L. Xinyanga,
“Error analysis of Gaussian spot width measured with CCD sensor,”
Proc. SPIE, 8417 841720
(2012). http://dx.doi.org/10.1117/12.970553 PSISDG 0277-786X Google Scholar
G. Mana, E. Massa and A. Rovera,
“Accuracy of laser beam center and width calculations,”
Appl. Opt., 40
(9), 1378
–1385
(2001). http://dx.doi.org/10.1364/AO.40.001378 APOPAI 0003-6935 Google Scholar
“Lasers and laser related equipment-Test methods for laser beam parameters-Beam widths, divergence angles and beam propagation ratios,”
(1999). Google Scholar
M. L. Boas, Mathematical Methods in the Physical Sciences, Wiley, New York
(1966). Google Scholar
BiographyLucas R. Hofer is a graduate student at the Universität Stuttgart, holding a fellowship from the International Max Planck Research School for Condensed Matter and was formerly a technical scientist at DataRay Inc. He received his BS degree in physics from the University of California, Los Angeles, USA, in 2015. He is the author of one journal paper detailing an innovative Mach–Zehnder interferometer control system. Rocco V. Dragone is the CTO and VP of engineering at DataRay Inc. He received his BS and MS degrees in electrical engineering from Drexel University in 2008. His current area of interest is laser beam profiling. Andrew D. MacGregor has a BSc degree in physics and a PhD in instrumentation for IR Astronomy from Imperial College, University of London. After work on IR imaging systems at Marconi Avionics and in fiber optic sensors, he joined RCA New Products in Quebec. Avalanche photodiode teamwork led to record sensitivity for intersatellite digital optical receivers and the first TTL output single photon counting module. Since 1998, he has proudly supported DataRay’s laser beam profiling instrumentation. He is a member of SPIE, OSA, and IEEE LEOS. |

